Кругова діаграма
У цій статті ви дізнаєтесь, що таке кругова діаграма, як побудувати кругову діаграму та покроково розглянемо вправу для цього типу діаграми. Крім того, ви зможете побачити характеристики кругових діаграм.
Що таке кругова діаграма?
Кругова діаграма , також звана круговою діаграмою , — це тип статистичної діаграми, який використовується для візуального представлення відсотків і пропорцій. Точніше, на круговій діаграмі дані представлені частинами кола, так що кут кожного сиру пропорційний його частоті.
Отже, чим вища частота значення, тим більшу частку воно займає в секторній діаграмі.

У статистиці секторні діаграми дуже корисні для представлення якісних даних на графіку, а також дозволяють швидко робити висновки.
Слід зазначити, що кругова діаграма має багато різних назв, таких як кругова діаграма, діаграма для піци, кругова діаграма, сирна діаграма або навіть 360-градусна діаграма.
Як зробити кругову діаграму
З огляду на визначення кругової діаграми, у цьому розділі показано, як створити діаграму цього типу:
- Зберіть статистичні дані та підготуйте відповідну частотну таблицю.
- Обчисліть кут кожного сектора графіка за такою формулою
- За обчисленими кутами зобразіть сектори на круговому графіку за допомогою транспортира.
- Обчисліть відсоток кожного сектора за такою формулою:
- Позначте на графіку відсоток кожного сектора.
![]()
золото
![]()
– кут сектора i ,
![]()
його абсолютна частота і
![]()
загальна кількість даних.
![]()
золото
![]()
є відсотком сектора i ,
![]()
його абсолютна частота і
![]()
загальна кількість даних.
Приклад секторної діаграми
Щоб ви могли побачити, як будується кругла діаграма, я залишу вам приклад, який крок за кроком пояснюється нижче.
- 50 людей запитали про їх улюблене місто, і дані були зібрані в наступній таблиці. Нанесіть ці статистичні дані на кругову діаграму.

Перш за все, ви повинні знайти кут, який відповідає кожному сиру . Для цього застосовуємо таку формулу:
![]()
золото
![]()
кут кожного сектора,
![]()
його частота і
![]()
загальна кількість спостережень.
Як приклад, обчислюється кут, що відповідає першому значенню в таблиці даних:
![]()
Як тільки ми знаємо кут, просто представимо круговий сектор за допомогою транспортира:
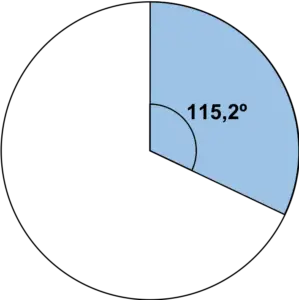
Повторюємо той же крок для всіх значень в таблиці:
![]()
![]()
![]()
![]()
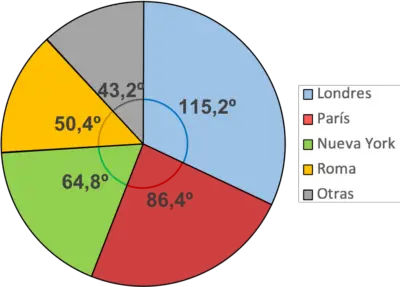
Рекомендується пофарбувати кожен сектор кольором, щоб полегшити розуміння графіка. Так само вам слід додати легенду, щоб показати значення кожного кольору на діаграмі.
Побудувавши сири на графіку, нам потрібно обчислити відсоток кожного з них, щоб помістити його на діаграму. Для цього використовуємо таку формулу:
![]()
золото
![]()
це відсоток кожного сектора,
![]()
його частота і
![]()
загальна кількість даних статистичного дослідження.
Отже, відсоток кожного сектора становить:
![]()
![]()
![]()
![]()
![]()
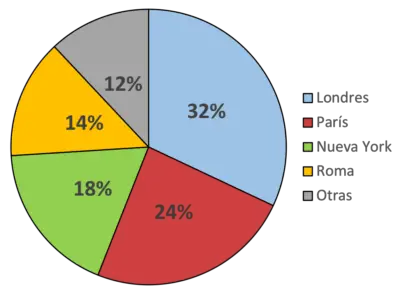
За допомогою цієї кругової діаграми ми вказуємо, що, наприклад, блакитний колір представляє місто Лондон і це місце, яке надає перевагу більшість людей (32% людей). З іншого боку, зелений колір представляє Нью-Йорк, який є улюбленим містом 18% опитаних.
Особливості кругової діаграми
Характеристики камамбера наступні:
- Кругова діаграма дуже корисна для представлення якісних даних.
- Однак існують інші типи статистичних графіків, які більше підходять для представлення кількісних змінних або часових рядів.
- Крім того, лише одна змінна може бути представлена на круговій діаграмі, що ускладнює порівняння змінних.
- Кругова діаграма дуже наочна, що дозволяє швидко аналізувати та робити висновки.
- Читання діаграми складно, якщо є багато секторів або деякі дуже малі. У такому випадку рекомендується згрупувати маленькі сектори в один сектор під назвою «Інші».