Кумулятивна частота

У цій статті пояснюється, що таке сукупна частота в статистиці. Отже, ви дізнаєтеся значення кумулятивної частоти, як розраховується кумулятивна частота на прикладах і, нарешті, різні типи кумулятивних частот, які існують.

Що таке кумулятивна частота?

У статистиці кумулятивна частота – це кумулятивна сума частот. Тобто кумулятивна частота значення дорівнює частоті цього значення плюс частоти всіх нижчих значень.

Існує два типи кумулятивних частот: кумулятивна абсолютна частота та кумулятивна відносна частота. Нижче ми побачимо, як обчислюється кожен тип сукупної частоти.

Майте на увазі: щоб зрозуміти, що означає кумулятивна частота в статистиці, ви повинні спочатку чітко знати концепцію частоти. Ось чому рекомендується відвідати наступну публікацію, перш ніж продовжити пояснення:

Як розрахувати кумулятивну частоту

Кроки для обчислення кумулятивної частоти статистичної вибірки:

1. Створіть таблицю з усіма різними значеннями, які з’являються в наборі даних, у порядку від найменшого до найбільшого.
2. Знайдіть абсолютну частоту кожного значення.
3. Знайдіть кумулятивну частоту кожного значення, яка обчислюється додаванням частоти самого значення плюс частоти всіх менших значень.

Отже, формула для розрахунку кумулятивної частоти така:

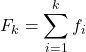
золото:

• 

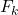
  є кумулятивною частотою значення

  

  .

• 

  це абсолютна частота значення

  

  .

Зверніть увагу, що ці кроки призначені для обчислення сукупної абсолютної частоти, але існує також сукупна відносна частота. Нижче ми побачимо різницю між цими двома типами накопичених частот і спосіб визначення кожного типу.

Типи кумулятивних частот

У статистиці існує два типи кумулятивних частот :

• Кумулятивна абсолютна частота : це кумулятивна сума абсолютних частот .
• Кумулятивна відносна частота : це кумулятивна сума відносних частот .

Розглядаючи визначення кожного типу накопиченої частоти, ви можете побачити нижче приклад того, як кожна з них отримана.

Кумулятивна абсолютна частота

Кумулятивна абсолютна частота представлена символом F _i і обчислюється шляхом додавання абсолютних частот значень, що дорівнюють або менше відповідного значення. Далі у вас є конкретний приклад, у якому обчислюється кумулятивна абсолютна частота набору статистичних даних.

• Оцінки, отримані з предмету статистика у класі, який налічує 30 учнів, такі. Яка сукупна абсолютна частота кожної ноти?

Оскільки всі числа можуть бути лише цілими, це дискретна змінна. Тому немає необхідності групувати дані в інтервали.

Отже, щоб визначити кумулятивну абсолютну частоту, ми повинні спочатку знайти абсолютну частоту кожного значення, яка є кількістю разів, коли кожне значення з’являється в статистичній вибірці.

Тепер, коли ми знаємо абсолютну частоту кожного значення, ми можемо обчислити їх кумулятивні абсолютні частоти. Для цього у нас є два варіанти: або ми додаємо абсолютну частоту значення плюс усі абсолютні частоти найменших значень, або, навпаки, ми додаємо абсолютну частоту значення плюс кумулятивну абсолютну частоту попередніх значень . значення.

Коротко кажучи, таблиця з абсолютною сукупною частотою вправ така:

Зверніть увагу, що накопичена абсолютна частота останнього значення завжди збігається із загальною кількістю даних. Інакше це означає, що ви помилилися в розрахунках.

Кумулятивна відносна частота

Кумулятивна відносна частота представлена символом H _i і розраховується шляхом додавання відносних частот значень, що дорівнюють або менше відповідного значення. Нижче ви можете побачити вправу, розв’язану з тими самими даними, що й попередня задача, у якій визначається кумулятивна відносна частота.

• Оцінки, отримані за статистикою в класі з 30 учнів, такі. Яка кумулятивна відносна частота кожної ноти?

У цьому випадку змінна є дискретною, оскільки не може приймати десяткове значення. Тому немає потреби групувати дані за інтервалами, але ми можемо виконувати обчислення безпосередньо.

Отже, складаємо таблицю частот і визначаємо абсолютну частоту кожного окремого значення:

Далі ми обчислюємо відносну частоту кожного значення, яка визначається діленням абсолютної частоти на загальну кількість спостережень (30).

І коли ми обчислили абсолютну частоту та відносну частоту набору даних, ми можемо отримати кумулятивну відносну частоту. Щоб зробити це, ви повинні додати відносну частоту відповідного значення плюс усі попередні відносні частоти або, що дорівнює тому ж самому, попередню накопичену відносну частоту:

Коротко кажучи, частотна таблиця з абсолютною частотою, відносною частотою та кумулятивною відносною частотою виглядає наступним чином:

Майте на увазі, що останнє значення кумулятивної відносної частоти завжди має бути 1. Якщо ви отримуєте інше число, це означає, що ви помилилися в розрахунках.