Вступ до регресії ласо

У звичайній множинній лінійній регресії ми використовуємо набір із p предикторних змінних і змінну відповіді , щоб відповідати моделі такого вигляду:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

золото:

• Y : змінна відповіді
• X _j : j- ^та прогнозна змінна
• β _j : середній вплив на Y від збільшення X _j на одну одиницю, утримуючи всі інші предиктори фіксованими
• ε : термін помилки

Значення β ₀ , β ₁ , B ₂ , …, β _p вибираються методом найменших квадратів , який мінімізує суму квадратів нев’язок (RSS):

RSS = Σ(y _i – ŷ _i ) ²

золото:

• Σ : грецький символ, що означає суму
• y _i : фактичне значення відповіді для ^i-го спостереження
• ŷ _i : прогнозоване значення відповіді на основі моделі множинної лінійної регресії

Однак, коли прогностичні змінні сильно корельовані, мультиколінеарність може стати проблемою. Це може зробити оцінки коефіцієнтів моделі ненадійними та мати високу дисперсію. Тобто, коли модель застосовується до нового набору даних, який вона ніколи раніше не бачила, вона, ймовірно, працюватиме погано.

Один із способів обійти цю проблему — використовувати метод, відомий як регресія ласо , який натомість намагається мінімізувати наступне:

RSS + λΣ|β _j |

де j змінюється від 1 до p і λ ≥ 0.

Цей другий член у рівнянні відомий як штраф за вилучення .

Коли λ = 0, цей штраф не має ефекту, і регресія ласо дає ті самі оцінки коефіцієнта, що й метод найменших квадратів.

Однак, коли λ наближається до нескінченності, штраф за видалення стає більш впливовим, а передбачувані змінні, які не можна імпортувати в модель, зменшуються до нуля, а деякі навіть видаляються з моделі.

Навіщо використовувати регресію Ласо?

Перевагою ласо-регресії над регресією найменших квадратів є компроміс зміщення-дисперсії .

Пам’ятайте, що середня квадратична помилка (MSE) – це показник, який ми можемо використовувати для вимірювання точності даної моделі, і він обчислюється таким чином:

MSE = Var( f̂( x ₀ )) + [Зміщення( f̂( x ₀ ))] ² + Var(ε)

MSE = дисперсія + зсув ² + незнижувана помилка

Основна ідея ласо-регресії полягає в тому, щоб ввести невелике зміщення, щоб дисперсію можна було значно зменшити, що призводить до нижчого загального середнього квадратичного значення.

Щоб проілюструвати це, розглянемо наступний графік:

Зверніть увагу, що зі збільшенням λ дисперсія значно зменшується з дуже невеликим збільшенням зміщення. Однак після певної точки дисперсія зменшується менш швидко і зменшення коефіцієнтів призводить до їх значного недооцінювання, що призводить до різкого збільшення зміщення.

З графіка ми бачимо, що MSE тесту є найнижчим, коли ми вибираємо значення для λ, яке забезпечує оптимальний компроміс між упередженням і дисперсією.

Коли λ = 0, штрафний термін у ласо-регресії не має ефекту, тому дає ті самі оцінки коефіцієнта, що й метод найменших квадратів. Однак, збільшивши λ до певної точки, ми можемо зменшити загальну MSE тесту.

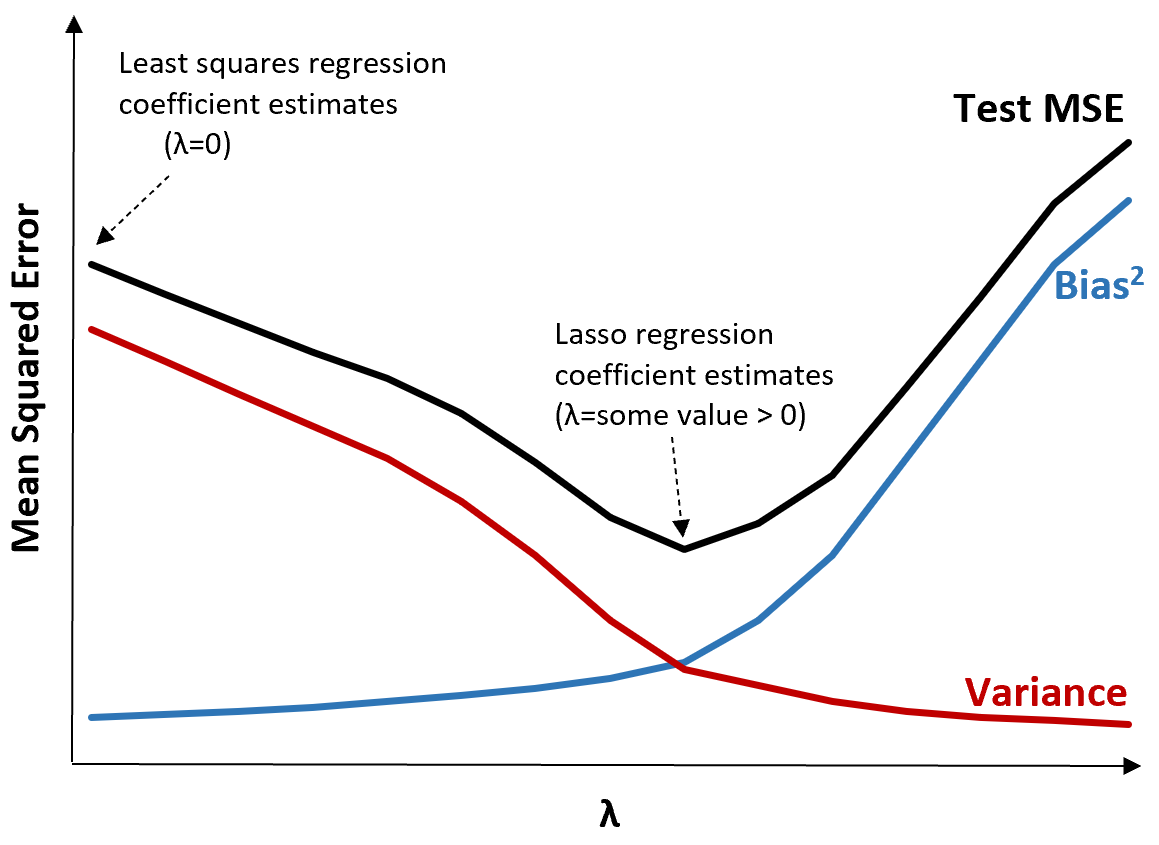
Це означає, що підгонка моделі за допомогою регресії ласо призведе до менших помилок тесту, ніж підгонка моделі за допомогою регресії найменших квадратів.

Регресія ласо проти регресії Ріджа

Регресія ласо та регресія Ріджа відомі як методи регулярізації , оскільки вони намагаються мінімізувати залишкову суму квадратів (RSS), а також певний термін штрафу.

Іншими словами, вони обмежують або регуляризують оцінки коефіцієнтів моделі.

Однак терміни покарання, які вони використовують, дещо інші:

• Регресія ласо намагається мінімізувати RSS + λΣ|β _j |
• Регресія хребта намагається мінімізувати RSS + λΣβ _j ²

Коли ми використовуємо гребеневу регресію, коефіцієнти кожного предиктора зменшуються до нуля, але жоден з них не може повністю обнулитися .

І навпаки, коли ми використовуємо ласо-регресію, можливо, що деякі коефіцієнти стають повністю нульовими , коли λ стає достатньо великим.

З технічної точки зору, ласо-регресія здатна створювати «розріджені» моделі, тобто моделі, які включають лише підмножину змінних предиктора.

У зв’язку з цим постає запитання: ридж-регресія чи ласо-регресія краще?

Відповідь: залежить!

У випадках, коли лише невелика кількість змінних предиктора є значущою, ласо-регресія, як правило, працює краще, оскільки вона здатна повністю звести незначущі змінні до нуля та видалити їх із моделі.

Однак, коли багато змінних предикторів є значущими в моделі, а їхні коефіцієнти приблизно рівні, гребенева регресія, як правило, працює краще, оскільки вона зберігає всі предиктори в моделі.

Щоб визначити, яка модель найбільш ефективна для прогнозування, ми виконуємо k-кратну перехресну перевірку . Яка б модель не дає найменшу середню квадратичну помилку (MSE), є найкращою моделлю для використання.

Етапи виконання ласо-регресії на практиці

Для виконання регресії ласо можна використати наступні кроки:

Крок 1: обчисліть кореляційну матрицю та значення VIF для змінних предиктора.

По-перше, нам потрібно створити кореляційну матрицю та обчислити значення VIF (коефіцієнт інфляції дисперсії) для кожної змінної предиктора.

Якщо ми виявимо сильну кореляцію між змінними предикторів і високими значеннями VIF (деякі тексти визначають «високе» значення VIF як 5, тоді як інші використовують 10), тоді ласо-регресія, ймовірно, підходить.

Однак, якщо в даних немає мультиколінеарності, може не виникнути потреби виконувати ласо-регресію. Замість цього ми можемо виконати звичайну регресію методом найменших квадратів.

Крок 2. Підберіть регресійну модель ласо та виберіть значення для λ.

Як тільки ми визначимо, що ласо-регресія підходить, ми зможемо підібрати модель (за допомогою популярних мов програмування, таких як R або Python), використовуючи оптимальне значення для λ.

Щоб визначити оптимальне значення для λ, ми можемо підібрати кілька моделей, використовуючи різні значення для λ, і вибрати λ як значення, яке дає найнижчий тест MSE.

Крок 3: Порівняйте регресію ласо з регресією хребта та звичайною регресією найменших квадратів.

Нарешті, ми можемо порівняти нашу регресійну модель ласо з моделлю хребтової регресії та регресійною моделлю найменших квадратів, щоб визначити, яка модель дає найнижчий тест MSE, використовуючи k-кратну перехресну перевірку.

Залежно від співвідношення між змінними прогнозу та змінною відповіді, цілком можливо, що одна з цих трьох моделей перевершить інші в різних сценаріях.

Регресія ласо в R & Python

У наступних посібниках пояснюється, як виконувати регресію ласо в R і Python:

Регресія ласо в R (покроково)
Регресія ласо в Python (крок за кроком)