Вступ до логістичної регресії

Коли ми хочемо зрозуміти зв’язок між однією або декількома змінними предиктора та змінною безперервної відповіді, ми часто використовуємо лінійну регресію .

Однак, коли змінна відповіді є категоричною, ми можемо використовувати логістичну регресію .

Логістична регресія — це тип алгоритму класифікації , оскільки він намагається «класифікувати» спостереження в наборі даних за різними категоріями.

Ось кілька прикладів використання логістичної регресії:

• Ми хочемо використовувати кредитну оцінку та банківський баланс , щоб передбачити, чи даний клієнт не виплатить кредит. (Змінна відповіді = «За замовчуванням» або «Немає за замовчуванням»)
• Ми хочемо використовувати середні підбирання за гру та середні очки за гру , щоб передбачити, чи буде даний баскетболіст задрафтований до НБА (змінна відповіді = «Задрафтований» або «Незадрафтований»).
• Ми хочемо використовувати квадратні метри та кількість ванних кімнат , щоб передбачити, чи буде будинок у певному місті виставлений за ціною продажу 200 000 доларів або більше. (Змінна відповіді = «Так» або «Ні»)

Зверніть увагу, що змінна відповіді в кожному з цих прикладів може приймати лише одне з двох значень. Порівняйте це з лінійною регресією, в якій змінна відповіді приймає безперервне значення.

Рівняння логістичної регресії

Логістична регресія використовує метод, відомий як оцінка максимальної правдоподібності (подробиці тут не обговорюватимуться), щоб знайти рівняння такої форми:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

золото:

• X _j : j- ^та прогнозна змінна
• β _j : оцінка коефіцієнта для j ^-ї прогностичної змінної

Формула в правій частині рівняння передбачає логарифмічні шанси того, що змінна відповіді набере значення 1.

Отже, коли ми підбираємо модель логістичної регресії, ми можемо використовувати наступне рівняння для обчислення ймовірності того, що дане спостереження набуває значення 1:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Потім ми використовуємо певний поріг ймовірності, щоб класифікувати спостереження як 1 або 0.

Наприклад, можна сказати, що спостереження з імовірністю, більшою або рівною 0,5, будуть класифіковані як «1», а всі інші спостереження будуть класифіковані як «0».

Як інтерпретувати результат логістичної регресії

Припустімо, що ми використовуємо модель логістичної регресії, щоб передбачити, чи буде певний баскетболіст задрафтований до НБА, на основі його середніх підбирань за гру та середніх очок за гру.

Ось результат моделі логістичної регресії:

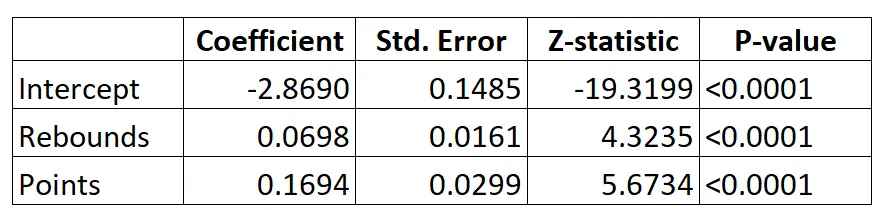
Використовуючи коефіцієнти, ми можемо розрахувати ймовірність того, що даний гравець буде задрафтований до НБА на основі його середніх підбирань і очок за гру за такою формулою:

P(Драфтований) = e ^{-2,8690 + 0,0698*(підбирання) + 0,1694*(очки)} / (1+e ^{-2,8690 + 0,0698*(підбирання) + 0,1694*(очки) ) )}

Наприклад, припустимо, що певний гравець робить у середньому 8 підбирань за гру та 15 очок за гру. Відповідно до моделі ймовірність того, що цього гравця задрафтують до НБА, становить 0,557 .

P(Письмовий) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15 )} ) = 0,557

Оскільки ця ймовірність перевищує 0,5, ми прогнозуємо, що цього гравця буде обрано.

Порівняйте це з гравцем, який в середньому робить лише 3 підбирання та 7 очок за гру. Імовірність того, що цього гравця задрафтують до НБА, становить 0,186 .

P(Письмовий) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7 )} ) = 0,186

Оскільки ця ймовірність менше 0,5, ми прогнозуємо, що цей гравець не буде обраний.

Припущення логістичної регресії

Логістична регресія використовує такі припущення:

1. Змінна відповіді є двійковою. Передбачається, що змінна відповіді може мати лише два можливі результати.

2. Спостереження незалежні. Передбачається, що спостереження в наборі даних не залежать одне від одного. Тобто спостереження не повинні походити від повторних вимірювань однієї особи або будь-яким чином пов’язані одне з одним.

3. Немає серйозної мультиколінеарності між змінними предикторів . Передбачається, що жодна з прогностичних змінних не сильно корелює одна з одною.

4. Екстремальних викидів немає. Передбачається, що в наборі даних немає екстремальних викидів або впливових спостережень.

5. Існує лінійна залежність між змінними предиктора та логітом змінної відповіді . Цю гіпотезу можна перевірити за допомогою тесту Бокса-Тідвелла.

6. Обсяг вибірки достатньо великий. Як правило, ви повинні мати щонайменше 10 випадків із найменш частим результатом для кожної пояснювальної змінної. Наприклад, якщо у вас є 3 пояснювальні змінні, а очікувана ймовірність найменш частого результату становить 0,20, тоді ви повинні мати розмір вибірки принаймні (10*3) / 0,20 = 150.

Перегляньте цю статтю , щоб отримати докладне пояснення того, як перевірити ці припущення.