Вступ до простої лінійної регресії

Проста лінійна регресія — це статистичний метод, який можна використовувати для розуміння зв’язку між двома змінними x і y.

Змінна x відома як змінна-прогноз .

Інша змінна, y , відома як змінна відповіді .

Наприклад, припустімо, що ми маємо такий набір даних із вагою та зростом семи осіб:

Нехай вага буде прогностичною змінною, а зріст – змінною відповіді.

Якщо ми побудуємо графік цих двох змінних за допомогою діаграми розсіювання з вагою на осі x і висотою на осі y, це виглядатиме ось як:

Припустимо, ми хочемо зрозуміти зв’язок між вагою та зростом. З діаграми розсіювання ми можемо чітко побачити, що зі збільшенням ваги зріст також має тенденцію до збільшення, але щоб фактично кількісно визначити це співвідношення між вагою та зростом, нам потрібно використовувати лінійну регресію.

Використовуючи лінійну регресію, ми можемо знайти лінію, яка найкраще «відповідає» нашим даним. Ця лінія відома як лінія регресії за методом найменших квадратів , і її можна використовувати, щоб допомогти нам зрозуміти зв’язок між вагою та зростом.

Зазвичай ви використовуєте таке програмне забезпечення, як Microsoft Excel, SPSS або графічний калькулятор, щоб знайти рівняння для цієї лінії.

Формула лінії найкращого прилягання записується:

ŷ = b ₀ + b ₁ x

де ŷ – прогнозоване значення змінної відповіді, b ₀ – відрізок, b ₁ – коефіцієнт регресії, а x – значення змінної предиктора.

За темою: 4 приклади використання лінійної регресії в реальному житті

Знайдіть «найкращу лінію»

Для цього прикладу ми можемо просто підключити наші дані до калькулятора статистичної лінійної регресії та натиснути «Обчислити» :

Калькулятор автоматично знаходить лінію регресії за методом найменших квадратів :

ŷ = 32,7830 + 0,2001x

Якщо ми зменшимо масштаб нашої попередньої діаграми розсіювання та додамо цей рядок до графіка, це виглядатиме ось як:

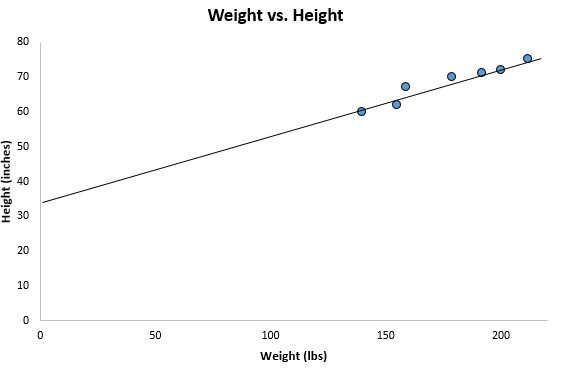
Зверніть увагу, як тісно розкидані наші точки даних навколо цієї лінії. Дійсно, ця лінія регресії найменших квадратів є лінією, яка найкраще підходить для наших даних серед усіх можливих ліній, які ми можемо намалювати.

Як інтерпретувати лінію регресії за методом найменших квадратів

Ось як інтерпретувати цю лінію регресії за методом найменших квадратів: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Це означає, що коли вага змінної прогнозу дорівнює нулю фунтів, прогнозована висота становить 32,7830 дюйма. Іноді значення b ₀ може бути корисним, але в цьому конкретному прикладі немає сенсу інтерпретувати b ₀ , оскільки людина не може важити нуль фунтів.

_b1 = 0,2001 . Це означає, що збільшення x на одну одиницю пов’язане зі збільшенням y на 0,2001 одиниці. У цьому випадку збільшення ваги на один фунт пов’язане зі збільшенням росту на 0,2001 дюйма.

Як використовувати лінію регресії за методом найменших квадратів

Використовуючи цю лінію регресії за методом найменших квадратів, ми можемо відповісти на такі запитання, як:

Якого зросту ми повинні очікувати для людини, яка важить 170 фунтів?

Щоб відповісти на це запитання, ми можемо просто вставити 170 у нашу лінію регресії для x і вирішити для y:

ŷ = 32,7830 + 0,2001(170) = 66,8 дюймів

Якого зросту ми повинні очікувати для людини, яка важить 150 фунтів?

Щоб відповісти на це запитання, ми можемо вставити 150 у лінію регресії для x і вирішити для y:

ŷ = 32,7830 + 0,2001(150) = 62,798 дюймів

Застереження: використовуючи рівняння регресії, щоб відповісти на подібні запитання, використовуйте лише значення для змінної предиктора, які знаходяться в межах діапазону змінної предиктора в наборі даних. початок, який ми використовували для створення лінії регресії за методом найменших квадратів. Наприклад, вага в нашому наборі даних коливалася від 140 до 212 фунтів. Тому має сенс відповідати на питання про очікуваний зріст, коли вага становить від 140 до 212 фунтів.

Коефіцієнт детермінації

Одним із способів вимірювання того, наскільки добре лінія регресії методом найменших квадратів «відповідає» даним, є використання коефіцієнта детермінації , який позначається як R ² .

Коефіцієнт детермінації — це частка дисперсії у змінній відповіді, яку можна пояснити змінною предиктора.

Коефіцієнт детермінації може змінюватися від 0 до 1. Значення 0 означає, що змінна відповіді взагалі не може бути пояснена змінною предиктора. Значення 1 вказує на те, що змінна відповіді може бути ідеально пояснена безпомилково змінною предиктора.

R ² між 0 і 1 вказує ступінь, до якої змінна відповіді може бути пояснена змінною предиктора. Наприклад, R ² 0,2 вказує на те, що 20% дисперсії у змінній відповіді можна пояснити змінною предиктора; R ² 0,77 вказує на те, що 77% дисперсії у змінній відповіді можна пояснити змінною предиктора.

Зверніть увагу, що в нашому попередньому результаті ми отримали R ² 0,9311, що вказує на те, що 93,11% мінливості зростання можна пояснити змінною предиктора ваги:

Це говорить нам про те, що вага є дуже хорошим показником росту.

Припущення лінійної регресії

Щоб результати моделі лінійної регресії були дійсними та надійними, ми повинні перевірити, чи виконуються такі чотири припущення:

1. Лінійний зв’язок: існує лінійний зв’язок між незалежною змінною x і залежною змінною y.

2. Незалежність: Залишки є незалежними. Зокрема, немає кореляції між послідовними залишками в даних часових рядів.

3. Гомоскедастичність: залишки мають постійну дисперсію на кожному рівні x.

4. Нормальність: модельні залишки розподілені нормально.

Якщо одне або декілька з цих припущень не виконуються, то результати нашої лінійної регресії можуть бути ненадійними або навіть оманливими.

Зверніться до цієї статті , щоб отримати пояснення щодо кожного припущення, як визначити, чи виконується припущення, і що робити, якщо припущення не виконується.