Як виконати тест тенденції манна-кендалла в r

Критерій тенденції Манна-Кендалла використовується, щоб визначити, чи є тенденція в даних часових рядів. Це непараметричний тест, тобто не робиться жодних базових припущень щодо нормальності даних.

Перевірені гіпотези такі:

H ₀ (нульова гіпотеза): у даних немає тенденції.

H _A (альтернативна гіпотеза): у даних наявна тенденція. (Це може бути як позитивна, так і негативна тенденція)

Якщо p-значення тесту є нижчим за певний рівень значущості (звичайними варіантами є 0,10, 0,05 і 0,01), то існує статистично значуще свідчення того, що в даних із часового ряду присутня тенденція.

У цьому посібнику пояснюється, як виконати тест тенденції Манна-Кендалла в R.

Приклад: тест тенденції Манна-Кендалла в R

Щоб виконати тест тенденції Манна-Кендалла в R, ми використаємо функцію MannKendall() із бібліотеки Kendall , яка використовує такий синтаксис:

МаннКендал (x)

золото:

• x = вектор даних, часто часовий ряд

Щоб проілюструвати, як виконати тест, ми використаємо вбудований набір даних PrecipGL бібліотеки Кендалл , який містить інформацію про річну кількість опадів для всіх Великих озер з 1900 по 1986 рік:

 #load Kendall library and PrecipGL dataset
library(Kendall)
data(PrecipGL)

#view dataset
PrecipGL

Time Series:
Start = 1900 
End = 1986 
Frequency = 1 
[1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61
[13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13
[25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34
[37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70
[49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38
[61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43
[73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97
[85] 32.15 40.16 36.32
attr(,"title")
[1] Annual precipitation, 1900-1986, Entire Great Lakes

Щоб побачити, чи є тенденція в даних, ми можемо виконати тест тенденції Манна-Кендалла:

 #Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00029206

Статистика тесту становить 0,265 , а відповідне двостороннє значення p — 0,00029206 . Оскільки це p-значення менше 0,05, ми відхилимо нульову гіпотезу тесту та зробимо висновок, що в даних присутній тренд.

Щоб візуалізувати тенденцію, ми можемо створити часовий графік річної кількості опадів за рік і додати плавну лінію для представлення тенденції:

 #Plot the time series data
plot(PrecipGL)

#Add a smooth line to visualize the trend 
lines(lowess(time(PrecipGL),PrecipGL), col='blue')

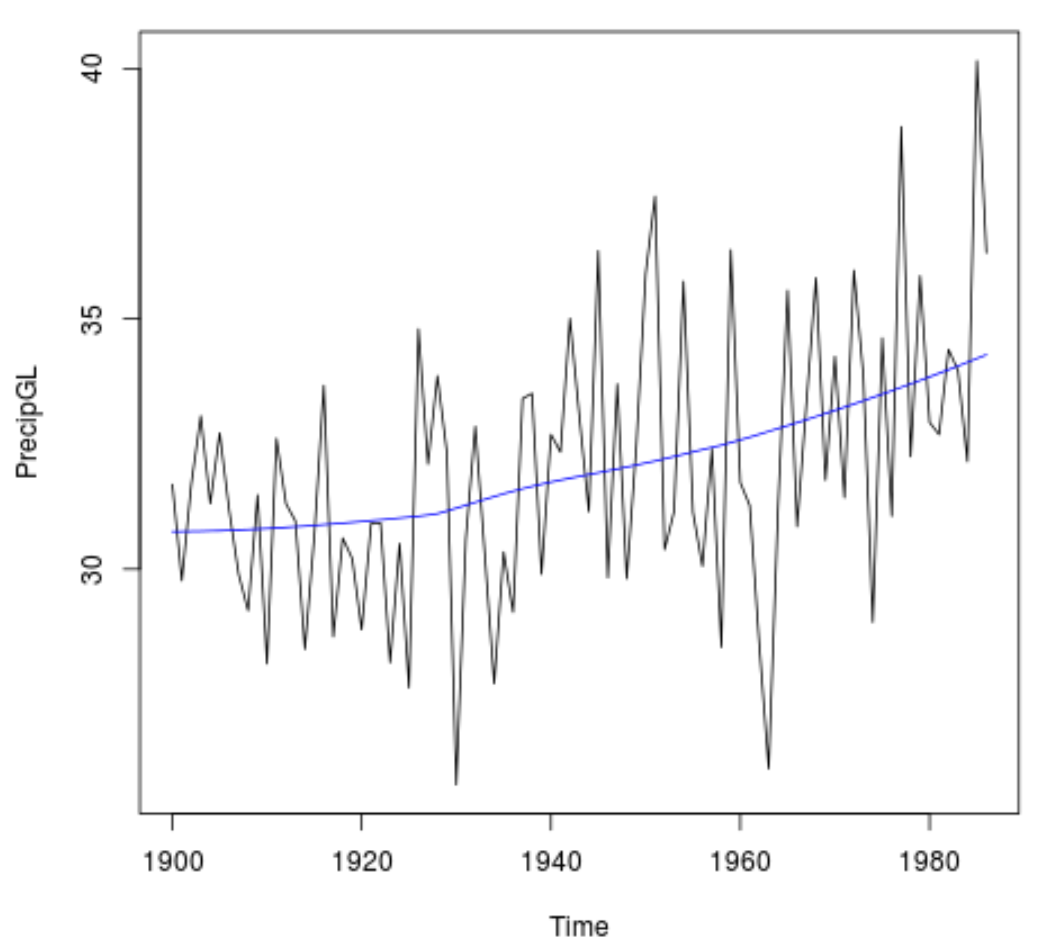
Зверніть увагу, що ми також можемо виконати сезонно скоригований тест тенденції Манна-Кендалла, щоб врахувати будь-яку сезонність у даних за допомогою команди SeasonalMannKendall(x) :

 #Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)

tau = 0.265, 2-sided pvalue = 0.00028797

Статистика тесту становить 0,265 , а відповідне двостороннє значення p — 0,00028797 . Знову це значення p менше 0,05, тому ми відхилимо нульову гіпотезу тесту та зробимо висновок, що в даних присутній тренд.