Множинна лінійна регресія вручну (крок за кроком)
Множинна лінійна регресія — це метод, який ми можемо використати для кількісного визначення зв’язку між двома чи більше змінними предикторами та змінною відповіді .
У цьому посібнику пояснюється, як вручну виконати множинну лінійну регресію.
Приклад: множинна лінійна регресія вручну
Припустімо, що ми маємо наступний набір даних зі змінною відповіді y і двома змінними-прогностиками x 1 і x 2 :
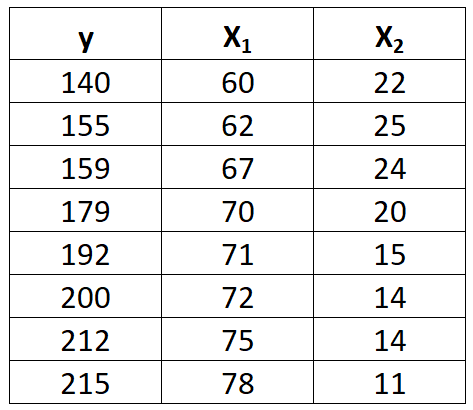
Виконайте наведені нижче кроки, щоб адаптувати модель множинної лінійної регресії до цього набору даних.
Крок 1: обчисліть x 1 2 , x 2 2 , x 1 y, x 2 y і x 1 x 2 .
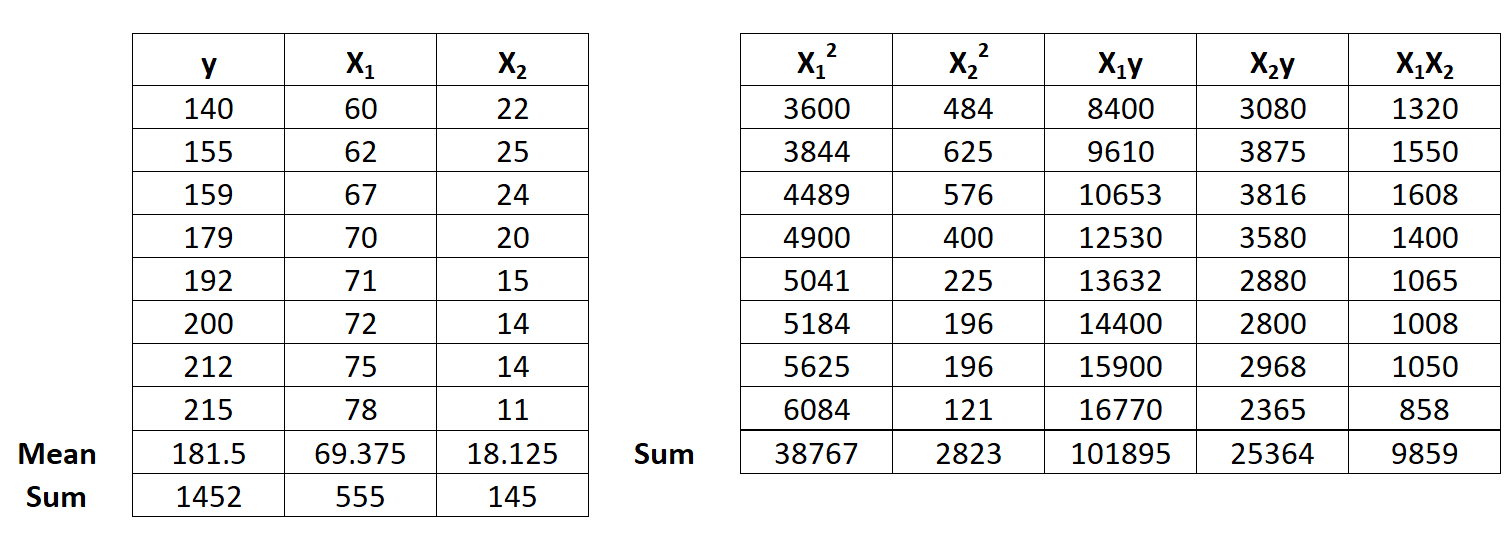
Крок 2: Обчисліть суми регресії.
Далі виконайте такі обчислення суми регресії:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ
- Σ x 2 y = Σ
- Σ x 1 x 2 = Σ
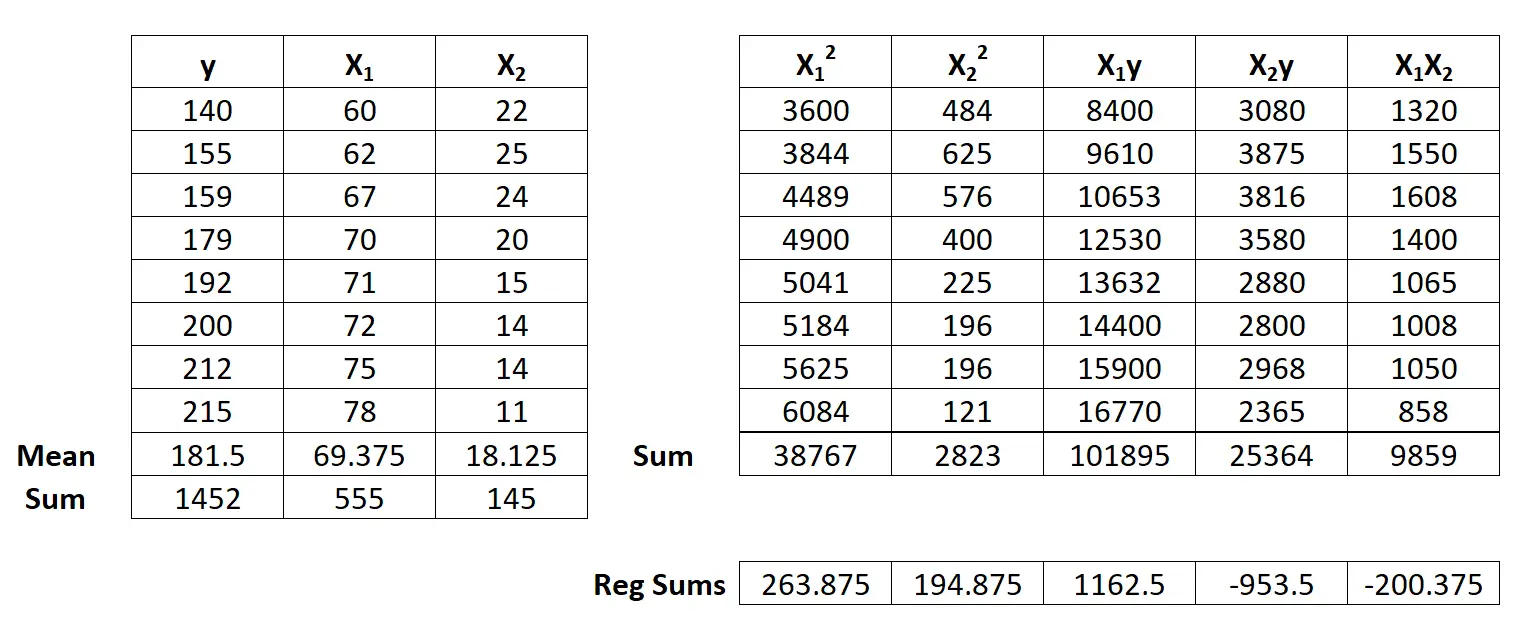
Крок 3: обчисліть b 0 , b 1 і b 2 .
Формула для обчислення b 1 така: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Отже, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
Формула для обчислення b 2 така: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Отже, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
Формула для обчислення b 0 така: y – b 1 X 1 – b 2 X 2
Таким чином, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Крок 5: Помістіть b 0 , b 1 і b 2 в оцінене рівняння лінійної регресії.
Розраховане рівняння лінійної регресії: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
У нашому прикладі це ŷ = -6,867 + 3,148x 1 – 1,656x 2
Як інтерпретувати рівняння множинної лінійної регресії
Ось як інтерпретувати це розраховане рівняння лінійної регресії: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Коли обидві змінні предиктора дорівнюють нулю, середнє значення y становить -6,867.
b1 = 3,148 . Збільшення x 1 на одну одиницю пов’язане зі збільшенням y на 3,148 одиниці в середньому, якщо припустити, що x 2 залишається постійним.
b2 = -1,656 . Збільшення x 2 на одну одиницю пов’язане зі зменшенням y на 1656 одиниць у середньому, якщо припустити, що x 1 залишається постійним.
Додаткові ресурси
Вступ до множинної лінійної регресії
Як виконати просту лінійну регресію вручну