Як виконати множинну лінійну регресію в excel

Множинна лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між двома або більше пояснювальними змінними та змінною відповіді .

У цьому посібнику пояснюється, як виконати множинну лінійну регресію в Excel.

Примітка. Якщо у вас є лише одна пояснювальна змінна, замість неї слід виконати просту лінійну регресію .

Приклад: Множинна лінійна регресія в Excel

Припустімо, ми хочемо знати, чи впливає кількість годин, витрачених на навчання, і кількість складених підготовчих іспитів на оцінку, яку отримує студент на певному вступному іспиті до коледжу.

Щоб дослідити цей зв’язок, ми можемо виконати множинну лінійну регресію, використовуючи вивчені години та підготовчі іспити як пояснювальні змінні, а результати іспитів – як змінну відповіді.

Виконайте наведені нижче дії в Excel, щоб виконати множинну лінійну регресію.

Крок 1: Введіть дані.

Про кількість вивчених годин, складених підготовчих іспитів та отриманих результатів іспитів для 20 студентів введіть такі дані:

Крок 2: Виконайте множинну лінійну регресію.

На верхній стрічці Excel перейдіть на вкладку «Дані» та натисніть «Аналіз даних» . Якщо ви не бачите цей параметр, спершу потрібно інсталювати безкоштовне програмне забезпечення Analysis ToolPak .

Коли ви натиснете «Аналіз даних», з’явиться нове вікно. Виберіть «Регресія» та натисніть «ОК».

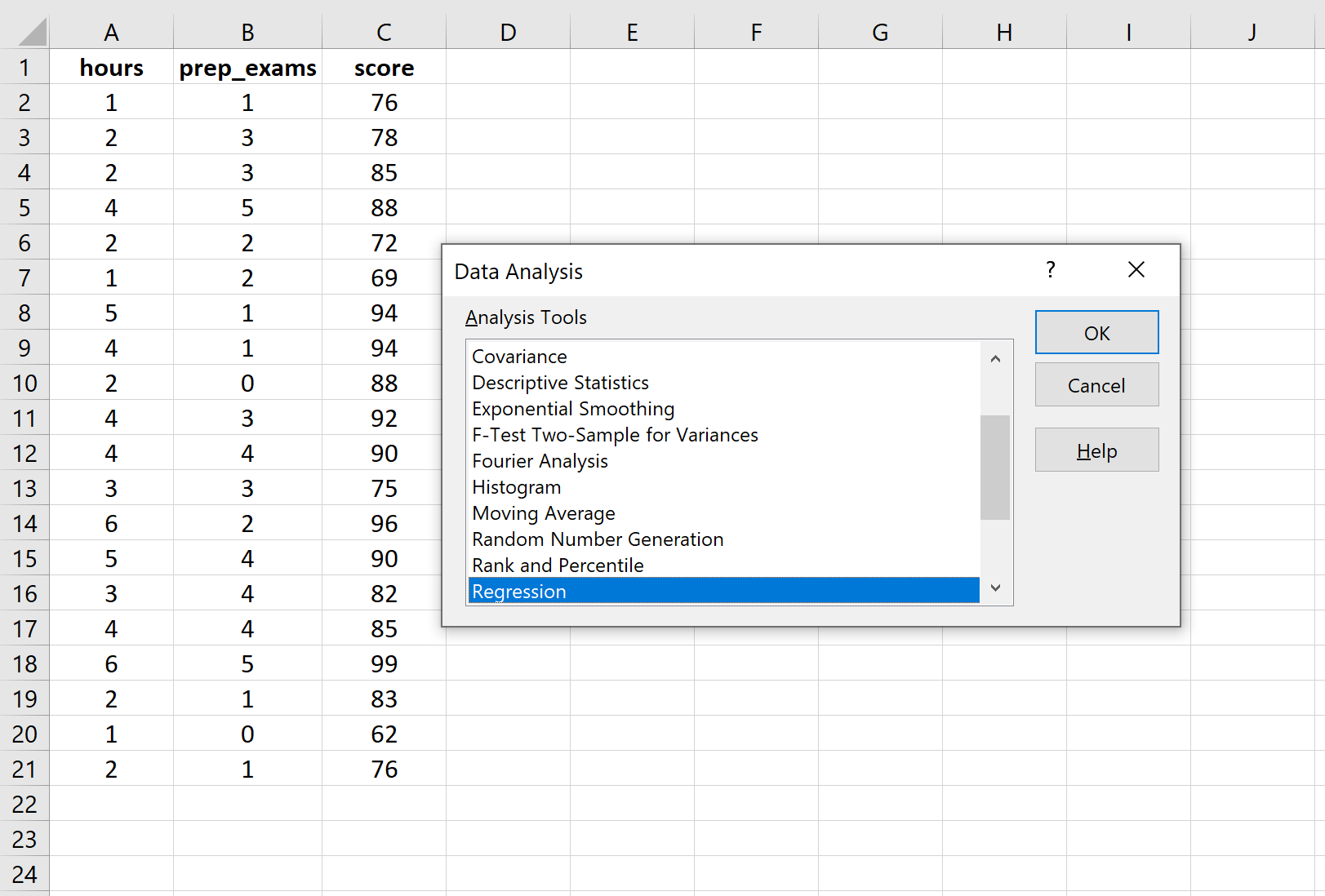
Для Input Y Range заповніть масив значень для змінної відповіді. Для Input X Range заповніть масив значень для двох пояснювальних змінних. Поставте прапорець біля пункту «Мітки» , щоб повідомити Excel, що ми включили імена змінних у вхідні діапазони. Для параметра «Діапазон результатів» виберіть комірку, у якій потрібно відобразити результат регресії. Потім натисніть OK .

Автоматично з’явиться такий результат:

Крок 3: Інтерпретація результату.

Ось як інтерпретувати найбільш відповідні числа в результаті:

Квадрат R: 0,734 . Це називається коефіцієнтом детермінації. Це частка дисперсії змінної відповіді, яку можна пояснити пояснювальними змінними. У цьому прикладі 73,4% розбіжностей в результатах іспитів пояснюється кількістю вивчених годин і кількістю складених підготовчих іспитів.

Стандартна похибка: 5,366 . Це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5366 одиниць від лінії регресії.

П: 23:46 Це загальна F-статистика для регресійної моделі, розрахована як регресійна MS/залишкова MS.

Значення F: 0,0000 . Це p-значення, пов’язане із загальною статистикою F. Це говорить нам про те, чи є модель регресії в цілому статистично значущою чи ні. Іншими словами, це повідомляє нам, чи дві пояснювальні змінні разом мають статистично значущий зв’язок зі змінною відповіді. У цьому випадку p-значення менше 0,05, що вказує на те, що пояснювальні змінні , години навчання та підготовчі іспити разом узяті , мають статистично значущий зв’язок із результатом іспиту .

Р-значення. Індивідуальні p-значення говорять нам, чи є кожна пояснювальна змінна статистично значущою чи ні. Ми бачимо, що години навчання є статистично значущими (p = 0,00), тоді як складені підготовчі іспити (p = 0,52) не є статистично значущими при α = 0,05. Оскільки минулі підготовчі іспити не є статистично значущими, ми можемо вирішити видалити їх із моделі.

Коефіцієнти: Коефіцієнти кожної пояснювальної змінної повідомляють нам очікувану середню зміну змінної відповіді, припускаючи, що інша пояснювальна змінна залишається постійною. Наприклад, за кожну додаткову годину, витрачену на навчання, очікується, що середній бал іспиту збільшиться на 5,56 , припускаючи, що складені практичні іспити залишаються незмінними.

Ось інший спосіб поглянути на це: якщо учень А та учень Б складають однакову кількість підготовчих іспитів, але учень А навчається на годину довше, тоді учень А має набрати на 5,56 бала більше, ніж учень Б.

Ми інтерпретуємо коефіцієнт перехоплення так, що очікуваний іспитовий бал для студента, який навчається без годин і не складає підготовчих іспитів, становить 67,67 .

Розрахункове рівняння регресії: ми можемо використати коефіцієнти з вихідних даних моделі, щоб створити наступне оцінюване рівняння регресії:

екзаменаційний бал = 67,67 + 5,56*(години) – 0,60*(підготовчі іспити)

Ми можемо використати це розраховане рівняння регресії, щоб обчислити очікуваний іспитовий бал для студента на основі кількості годин навчання та кількості практичних іспитів, які він складає. Наприклад, студент, який займається три години і складає підготовчий іспит, повинен отримати оцінку 83,75 :

бал = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Майте на увазі, що оскільки попередні підготовчі іспити не були статистично значущими (p=0,52), ми можемо вирішити їх видалити, оскільки вони не покращують загальну модель. У цьому випадку ми могли б виконати просту лінійну регресію, використовуючи лише досліджувані години як пояснювальну змінну.

Результати цього простого аналізу лінійної регресії можна знайти тут .

Додаткові ресурси

Виконавши множинну лінійну регресію, ви можете перевірити кілька припущень, зокрема:

1. Тестування на мультиколінеарність за допомогою VIF .

2. Тест на гетеродскедастичність за допомогою тесту Брейша-Пейгана .

3. Перевірте нормальність за допомогою графіка QQ .