Населення означає
У цій статті пояснюється, що означає населення в статистиці. Так само ви дізнаєтеся, що таке формула для середнього значення сукупності, як обчислюється довірчий інтервал середнього значення генеральної сукупності та, крім того, яка різниця між середнім значенням генеральної сукупності та середнім значенням вибірки.
Яка середня кількість населення?
Середня сукупність — це середнє арифметичне всіх елементів статистичної сукупності. Тому, щоб обчислити середнє значення генеральної сукупності, усі значення генеральної сукупності потрібно додати, а потім розділити на загальну кількість елементів у генеральній сукупності.
Символом середньої сукупності є грецька літера μ.
Подібним чином середнє значення генеральної сукупності також можна визначити як очікуване значення змінної, яка представляє генеральну сукупність.
Як розрахувати середнє населення
Після того, як ми ознайомилися з визначенням середньої сукупності, давайте подивимося, як обчислюється середня сукупність, щоб краще зрозуміти її значення.
Якщо відомі всі значення в статистичній сукупності, для розрахунку середньої сукупності слід просто застосувати формулу середнього арифметичного. Тож у цьому випадку, щоб обчислити середнє значення сукупності, нам потрібно скласти всі значення сукупності, а потім розділити на загальну кількість даних.
Таким чином, якщо ми знаємо значення всіх елементів генеральної сукупності, формула для розрахунку середнього генеральної сукупності виглядає наступним чином:
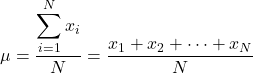
Однак, як правило, не всі значення сукупності відомі, тому зазвичай значення середньої сукупності оцінюють за інтервалами .
Довірчий інтервал для середнього значення сукупності
На практиці неможливо вивчити всіх особин у популяції, тому зазвичай вибирають випадкову вибірку популяції та на основі її значень роблять наближення значення середнього популяції. Точніше, ми обчислюємо інтервал, в якому, швидше за все, буде знаходитися середнє значення всієї сукупності; цей інтервал називається довірчим інтервалом для середньої сукупності.
Довірчий інтервал для середньої генеральної сукупності обчислюється шляхом додавання та віднімання від середнього значення Z α/2 , помноженого на стандартне відхилення (σ) і поділеного на квадратний корінь із висоти вибірки (n). Таким чином, формула для розрахунку довірчого інтервалу для середнього сукупності має вигляд:
![]()
Наведена вище формула використовується, коли відома дисперсія сукупності. Однак, якщо дисперсія генеральної сукупності невідома, що є найпоширенішим випадком, довірчий інтервал для середнього обчислюється за такою формулою:
![]()
золото:
-

це зразок засобів.
-

– значення t-розподілу Стьюдента n-1 ступенів свободи з імовірністю α/2. Для великих розмірів вибірки та 95% рівня довіри він зазвичай близький до 1,96, а для 99% рівня довіри він зазвичай близький до 2,576.
-

є стандартним відхиленням вибірки.
-

це розмір вибірки.
Середнє значення сукупності та вибіркове значення
Нарешті, підсумовуючи, ми розглянемо відмінності між середнім значенням сукупності та середнім значенням вибірки, щоб ці дві статистичні концепції були зрозумілими.
Різниця між середнім значенням сукупності та середнім значенням вибірки – це діапазон значень, за яким розраховується середнє. Середнє значення сукупності є середнім для всієї статистичної сукупності, тоді як середнє значення вибірки є середнім для вибірки сукупності.
Крім того, щоб відрізнити середнє значення генеральної сукупності від середнього вибіркового, їх позначають різними символами. Символ населення означає
![]()
, з іншого боку, символ зразка означає
![]()
.
![Rendered by QuickLaTeX.com \begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f812349b186d7c1a8abdd1d2807f0a60_l3.png)
Якщо у вас все ще є сумніви щодо відмінностей між цими двома типами середніх значень або ви хочете дізнатися більше про обчислення вибіркового середнього значення, ви можете ознайомитися з такою статтею: