Від’ємний біном проти пуассона: як вибрати модель регресії

Негативна біноміальна регресія та регресія Пуассона — це два типи моделей регресії, які слід використовувати, коли змінна відповіді представлена результатами дискретного підрахунку.

Ось кілька прикладів змінних відповідей, які представляють результати дискретного підрахунку:

• Кількість студентів, які закінчили певну програму
• Кількість ДТП на певному перехресті
• Кількість учасників, які закінчили марафон
• Кількість повернень у певний місяць у роздрібному магазині

Якщо дисперсія приблизно дорівнює середньому, то модель регресії Пуассона, як правило, добре відповідає набору даних.

Однак, якщо дисперсія значно перевищує середнє значення, модель негативної біноміальної регресії, як правило, може краще підібрати дані.

Є два методи, які ми можемо використати, щоб визначити, чи регресія Пуассона чи негативна біноміальна регресія є більш доречною для даного набору даних:

1. Залишкові ділянки

Ми можемо створити графік стандартизованих залишків проти прогнозованих значень з регресійної моделі.

Якщо більшість стандартизованих залишків становить від -2 до 2, модель регресії Пуассона, ймовірно, підійде.

Однак, якщо багато залишків виходять за межі цього діапазону, модель негативної біноміальної регресії, швидше за все, забезпечить кращу відповідність.

2. Тест співвідношення правдоподібності

Ми можемо підібрати модель регресії Пуассона та негативну біноміальну регресійну модель до одного набору даних, а потім виконати перевірку співвідношення правдоподібності.

Якщо p-значення тесту нижче певного рівня значущості (наприклад, 0,05), тоді можна зробити висновок, що негативна біноміальна регресійна модель забезпечує значно кращу відповідність.

У наступному прикладі показано, як використовувати ці дві методики в R, щоб визначити, чи краще використовувати регресію Пуассона чи негативну біноміальну регресійну модель для даного набору даних.

Приклад: негативна біноміальна регресія проти регресії Пуассона

Припустімо, ми хочемо знати, скільки стипендій отримує бейсболіст середньої школи в даному окрузі залежно від його шкільного класу («A», «B» або «C») і його шкільного класу. вступний іспит до ВНЗ (вимірюється від 0 до 100). ).

Виконайте наступні кроки, щоб визначити, чи модель негативної біноміальної регресії чи модель регресії Пуассона забезпечує кращу відповідність даним.

Крок 1: Створіть дані

Наступний код створює набір даних, з яким ми працюватимемо, який містить дані про 1000 бейсболістів:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Крок 2. Підберіть модель регресії Пуассона та модель негативної біноміальної регресії

У наведеному нижче коді показано, як пристосувати до даних як модель регресії Пуассона, так і модель негативної біноміальної регресії:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Крок 3: Створення залишкових ділянок

У наведеному нижче коді показано, як створити графіки залишків для обох моделей.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

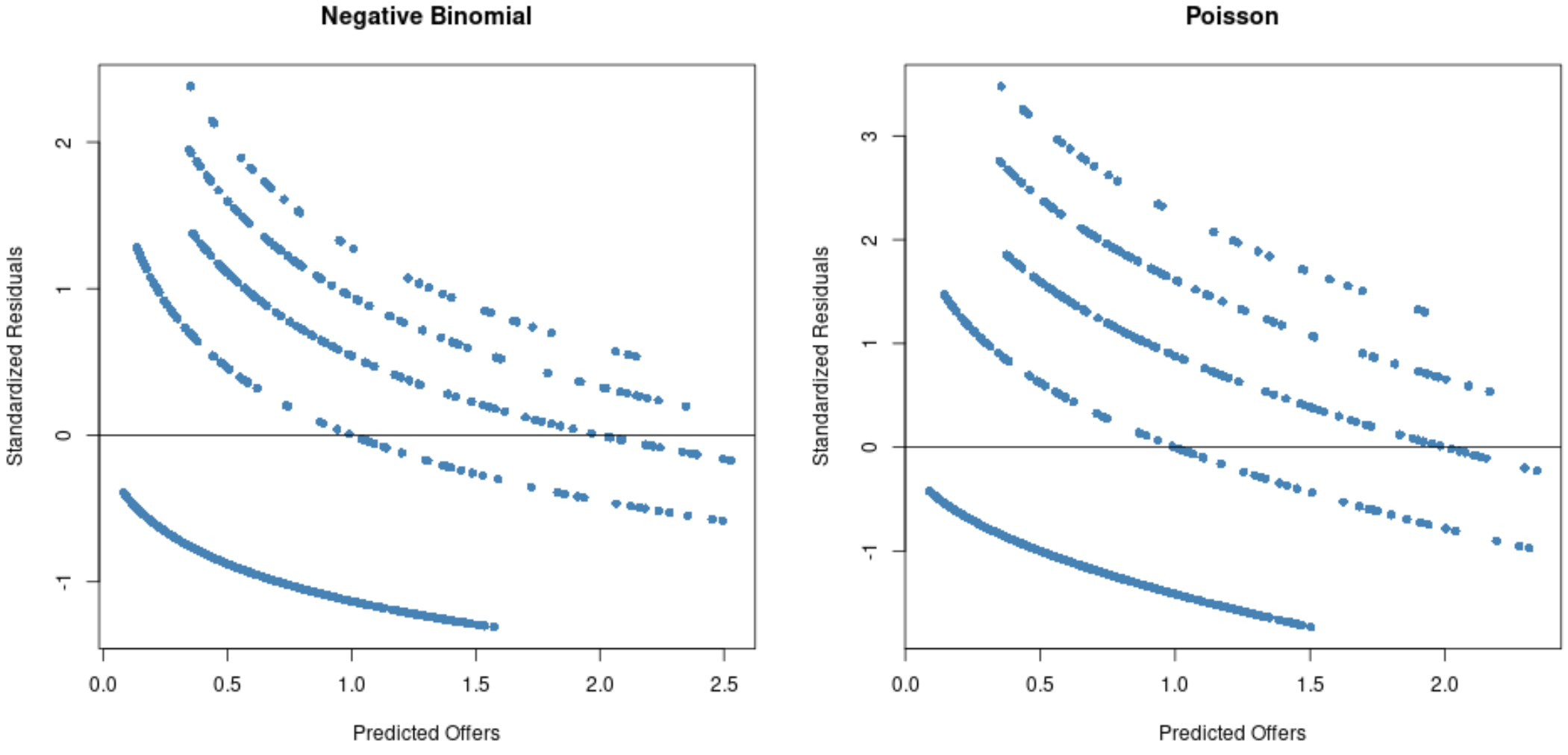
З графіків ми бачимо, що залишки більш розкидані для моделі регресії Пуассона (зверніть увагу, що деякі залишки виходять за межі 3) порівняно з моделлю негативної біноміальної регресії.

Це ознака того, що негативна біноміальна регресійна модель, ймовірно, більш доцільна, оскільки залишки цієї моделі менші.

Крок 4: Виконайте перевірку співвідношення правдоподібності

Нарешті, ми можемо виконати тест на відношення правдоподібності, щоб визначити, чи є статистично значуща різниця у відповідності двох регресійних моделей:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

P-значення тесту виявляється 3,508072e-29 , що значно менше, ніж 0,05.

Таким чином, можна зробити висновок, що модель негативної біноміальної регресії забезпечує значно кращу відповідність даних порівняно з моделлю регресії Пуассона.

Додаткові ресурси

Введення в негативний біноміальний розподіл
Введення в розподіл Пуассона