Нормальний чи рівномірний розподіл: у чому різниця?

Нормальний розподіл є найбільш часто використовуваним розподілом ймовірностей у статистиці.

Він має такі властивості:

• Симетричний
• У формі дзвоника

Якщо ми побудуємо графік нормального розподілу, він виглядатиме так:

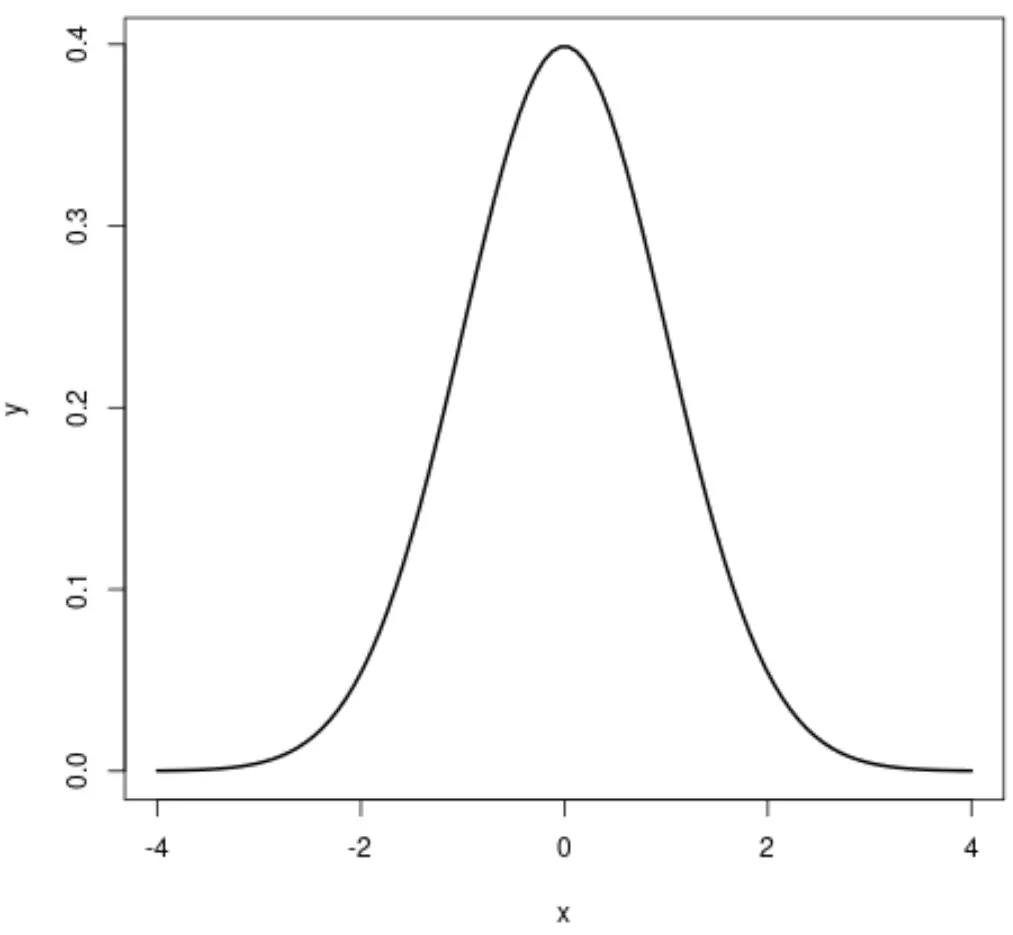
Рівномірний розподіл — це розподіл ймовірностей, у якому кожне значення між інтервалом від a до b має однакову ймовірність появи.

Він має такі властивості:

• Симетричний
• Прямокутної форми

Якщо ми побудуємо графік рівномірного розподілу, він буде виглядати так:

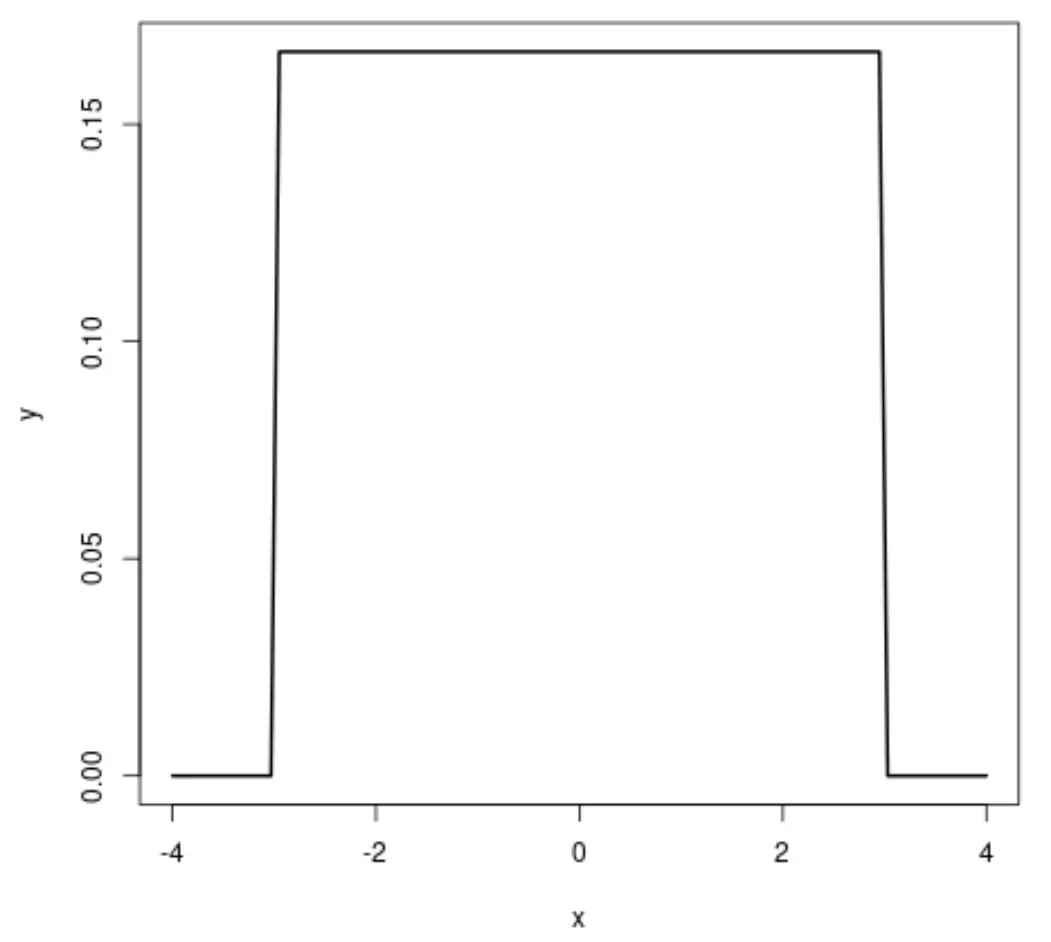
Нормальний розподіл і рівномірний розподіл мають таку схожість :

• Два розподіли є симетричними. Тобто, якщо ми проведемо лінію через центр розподілу, ліва і права сторони розподілу будуть ідеально віддзеркалювати одна одну:

Однак ці два розподіли мають такі відмінності :

• Розподіли мають різну форму.
• Нормальний розподіл має форму дзвона, що означає, що значення поблизу центру розподілу мають більшу ймовірність появи, ніж значення в хвостах розподілу.
• Рівномірний розподіл має форму прямокутника, що означає, що кожне значення в розподілі має однакову ймовірність появи.

Нормальний розподіл або рівномірний розподіл: коли їх використовувати?

Нормальний розподіл використовується для моделювання явищ, які мають тенденцію слідувати за формою «дзвоноподібної кривої». Наприклад, добре задокументовано, що вага новонароджених зазвичай розподіляється в середньому близько 7,5 фунтів.

Гістограма ваги новонароджених при народженні в США має дзвоноподібну форму, що в цілому відповідає нормальному розподілу:

Більшість немовлят, ймовірно, важать близько 7,5 фунтів, деякі важать менше 7 фунтів, а деякі важать більше 8 фунтів.

І навпаки, рівномірний розподіл використовується для моделювання сценаріїв, у яких кожен потенційний результат є однаково ймовірним.

Класичним прикладом є кидання кубика. Якщо ви кинете кубик один раз, ймовірність того, що він випаде на число від 1 до 6, розподіляється рівномірно, оскільки кожне число має однакову ймовірність появи.

Наприклад, існує 6 можливих чисел, на які може впасти кубик, тому ймовірність того, що ви кинете 1, становить 1/6.

Так само ймовірність того, що ви випадете 2, дорівнює 1/6.

Так само ймовірність того, що ви випадете 3, становить 1/6.

І так далі.

Бонус: як побудувати нормальний і рівномірний розподіл

Ми використали такий код у R, щоб створити графіки нормального та рівномірного розподілу:

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

Додаткові ресурси

6 конкретних прикладів нормального розподілу
5 конкретних прикладів рівномірного розподілу
Симетричний розподіл: визначення + приклади