Нормальний розподіл

Нормальний розподіл є найпоширенішим розподілом ймовірностей у статистиці.

Нормальний розподіл має такі характеристики:

• Форма дзвоника
• Симетричний
• Середнє та медіана рівні; обидва розташовані в центрі розподілу
• Близько 68% даних знаходяться в межах одного стандартного відхилення від середнього
• Близько 95% даних знаходяться в межах двох стандартних відхилень від середнього.
• Близько 99,7% даних знаходяться в межах трьох стандартних відхилень від середнього.

Останні три пункти відомі як емпіричне правило , яке іноді називають правилом 68-95-99.7 .

Пов’язане: Правило великого пальця (практичні питання)

Як намалювати нормальну криву

Щоб намалювати нормальну криву, нам потрібно знати середнє значення та стандартне відхилення.

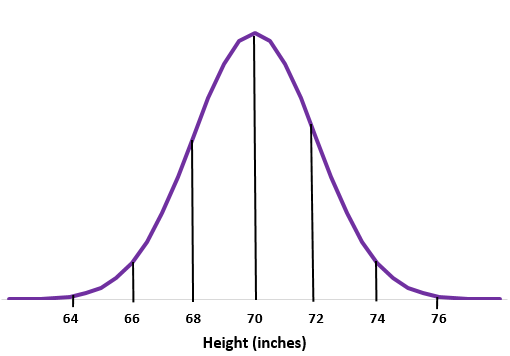
Приклад 1. Припустимо, що зріст чоловіків у певній школі зазвичай розподіляється із середнім значенням $\mu =\; 70\; дюймів\; і$ стандартним відхиленням $\sigma \; =\; 2\; дюйми.\; Намалюйте\; нормальну\; криву.$

Крок 1: Намалюйте нормальну криву.

Крок 2: Середнє значення 70 дюймів знаходиться посередині.

Крок 3: кожне стандартне відхилення відповідає відстані 2 дюйми.

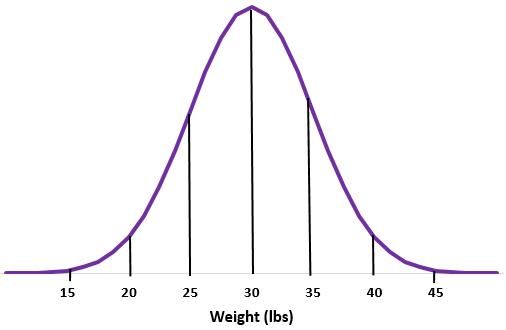
Приклад 2: Припустімо, що вага певного виду видри розподілена нормально із середнім значенням $\mu =\; 30\; фунтів\; і$ стандартним відхиленням $\sigma \; =\; 5\; фунтів.\; Намалюйте\; нормальну\; криву.$

Крок 1: Намалюйте нормальну криву.

Крок 2: Середня вага 30 фунтів знаходиться посередині.

Крок 3: кожне стандартне відхилення відповідає відстані 5 фунтів

Як знайти відсотки за допомогою нормального розподілу

Емпіричне правило , яке іноді називають правилом 68-95-99.7 , стверджує, що для нормально розподіленої випадкової змінної 68% даних потрапляє в діапазон одного стандартного відхилення від середнього, 95% потрапляє в діапазон двох стандартних відхилення від середнього значення та 99,7% знаходяться в межах трьох стандартних відхилень від середнього значення.

Використовуючи це правило, ми можемо відповісти на запитання про відсотки.

Приклад: припустимо, що зріст чоловіків у певній школі зазвичай розподіляється із середнім значенням $\mu =\; 70\; дюймів\; і$ стандартним відхиленням $\sigma \; =\; 2\; дюйми.$

$Приблизний\; відсоток\; чоловіків\; у\; цій\; школі\; мають\; зріст\; понад\; 74\; дюйми?$

рішення:

Крок 1: Намалюйте нормальний розподіл із середнім значенням $\mu =\; 70\; дюймів\; і$ стандартним відхиленням $\sigma \; =\; 2\; дюйми.$

Крок 2: Зріст 74 дюйми на два стандартні відхилення вище середнього. Додайте відсотки вище цієї точки до нормального розподілу.

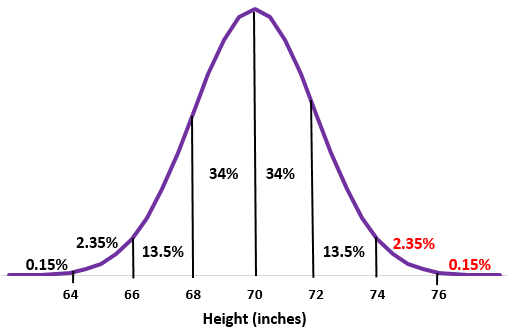
2,35% + 0,15% = 2,5%

Близько 2,5% чоловіків у цій школі мають зріст понад 74 дюйми.

$Який\; приблизно\; відсоток\; чоловіків\; у\; цій\; школі\; має\; зріст\; від\; 68\; до\; 72\; дюймів?$

рішення:

Крок 1: Намалюйте нормальний розподіл із середнім значенням $\mu =\; 70\; дюймів\; і$ стандартним відхиленням $\sigma \; =\; 2\; дюйми.$

Крок 2: Зріст 68 дюймів і 72 дюйми є на одне стандартне відхилення нижче і вище середнього відповідно. Просто додайте відсотки між цими двома точками в нормальному розподілі.

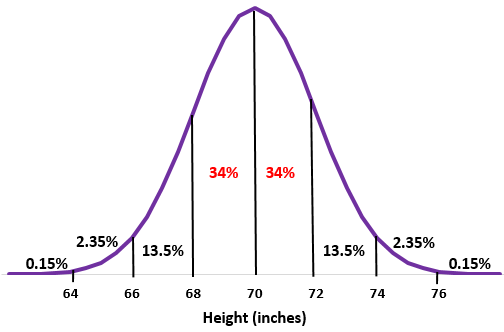
34% + 34% = 68%

Близько 68% чоловіків у цій школі мають зріст від 68 до 72 дюймів.

Як знайти підрахунки за допомогою нормального розподілу

Ми також можемо використовувати емпіричне правило, щоб відповісти на запитання про підрахунки.

Приклад: припустимо, що вага певного виду видри нормально розподілена із середнім значенням $\mu =\; 30\; фунтів\; і$ стандартним відхиленням $\sigma \; =\; 5\; фунтів.$

Певна колонія має 200 цих видр. Приблизно скільки з цих видр важать більше 35 фунтів?

рішення:

Крок 1: Намалюйте нормальний розподіл із середнім значенням $\mu =\; 30\; фунтів\; і$ стандартним відхиленням $\sigma \; =\; 5\; фунтів.$

Крок 2: вага 35 фунтів є одним стандартним відхиленням вище середнього. Додайте відсотки вище цієї точки до нормального розподілу.

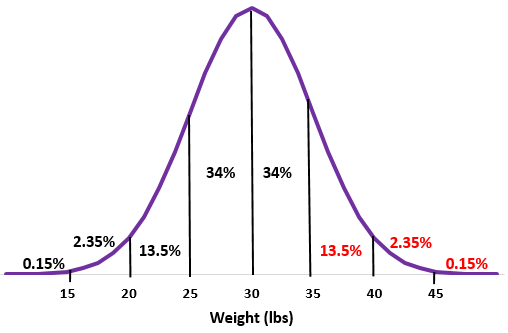
13,5% + 2,35% + 0,15% = 16%

Крок 3. Оскільки в колонії 200 видр, 16% від 200 = 0,16 * 200 = 32

Приблизно 32 видри в цій колонії важать більше 35 фунтів.

Приблизно скільки видр у цій колонії важать менше 30 фунтів?

Замість виконання всіх кроків, які ми щойно зробили вище, ми можемо визнати, що медіана нормального розподілу дорівнює середньому, яке в даному випадку становить 30 фунтів.

Це означає, що половина видр важить більше 30 фунтів, а інша половина важить менше 30 фунтів. Це означає, що 50% із 200 видр важать менше 30 фунтів, отже, 0,5 * 200 = 100 видр .

Додаткові ресурси

Наступні посібники надають додаткову інформацію про нормальний розподіл:

6 конкретних прикладів нормального розподілу
Нормальний розподіл проти t-розподілу: різниця
Як створити дзвоноподібну криву в Excel
Як створити дзвоноподібну криву в Python