Розуміння нульової гіпотези для моделей anova

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Односторонній ANOVA використовує такі нульові та альтернативні гіпотези:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (усі групові середні рівні)
• H _A : Принаймні одна середня група відрізняється   відпочинок

Щоб вирішити, чи варто нам відхиляти нульову гіпотезу чи ні, нам потрібно звернутися до значення p у результаті таблиці ANOVA.

Якщо p-значення нижче певного рівня значущості (наприклад, 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що не всі групові середні рівні.

Двосторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп, які були віднесені до двох змінних (іноді їх називають «факторами»).

Двосторонній ANOVA перевіряє три нульові гіпотези одночасно:

• Усі групові середні рівні на кожному рівні першої змінної
• Усі групові середні рівні на кожному рівні другої змінної
• Між двома змінними немає ефекту взаємодії

Щоб вирішити, чи варто нам відхиляти кожну нульову гіпотезу, нам потрібно звернутися до p-значень у результаті двосторонньої таблиці ANOVA.

У наведених нижче прикладах показано, як прийняти рішення про відхилення нульової гіпотези в односторонньому та двосторонньому дисперсійному аналізі.

Приклад 1: односторонній дисперсійний аналіз

Припустімо, ми хочемо знати, чи три різні програми підготовки до іспиту призводять до різних середніх балів на даному іспиті. Щоб перевірити це, ми набираємо 30 студентів для участі в дослідженні та ділимо їх на три групи.

Студенти в кожній групі випадковим чином розподіляються для використання однієї з трьох програм підготовки до іспиту протягом наступних трьох тижнів для підготовки до іспиту. Після закінчення трьох тижнів усі студенти складають один і той же іспит.

Результати іспитів для кожної групи наведені нижче:

Коли ми вводимо ці значення в односторонній калькулятор ANOVA , ми отримуємо на виході наступну таблицю ANOVA:

Зауважте, що p-значення становить 0,11385 .

Для цього конкретного прикладу ми б використали такі нульові та альтернативні гіпотези:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (середній бал за іспит для кожної групи однаковий)
• H _A : Принаймні одна середня група відрізняється   відпочинок

Оскільки p-значення таблиці ANOVA не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що існує статистично значуща різниця між середніми іспитовими балами трьох груп.

Приклад 2: Двосторонній дисперсійний аналіз

Припустімо, ботанік хоче знати, чи впливає на ріст рослин сонячне світло та частота поливу.

Вона висаджує 40 насінин і дає їм рости протягом двох місяців у різних умовах сонячного освітлення та частоти поливу. Через два місяці вона записує висоту кожної рослини. Результати наведені нижче:

У таблиці вище ми бачимо, що в кожній комбінації умов було вирощено п’ять рослин.

Наприклад, п’ять рослин вирощували з щоденним поливом і без сонячного світла, і їхня висота через два місяці становила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма та 4,4 дюйма:

Вона виконує двосторонній дисперсійний аналіз в Excel і отримує такий результат:

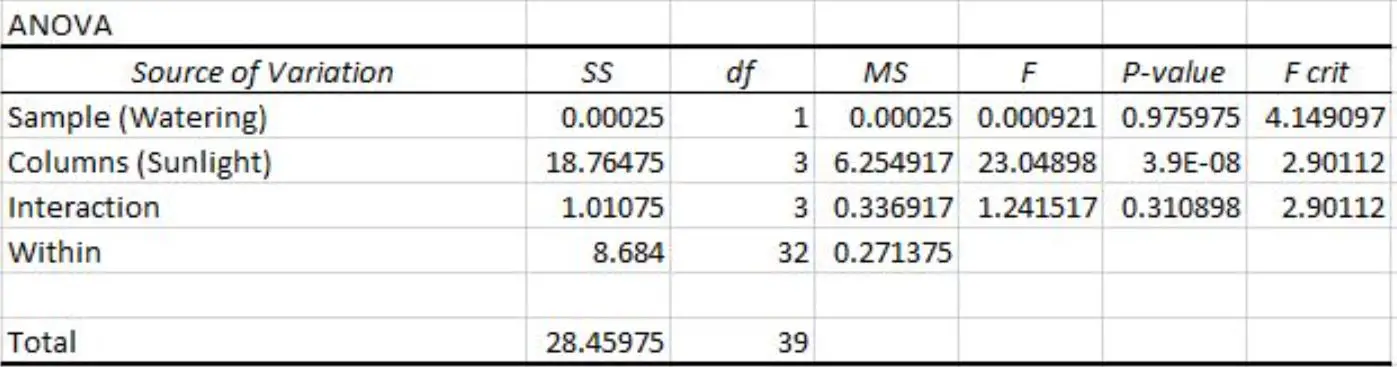
Ми можемо побачити наступні p-значення в результаті двосторонньої таблиці ANOVA:

• P-значення частоти поливу становить 0,975975 . Це не є статистично значущим на рівні значущості 0,05.
• P-значення для перебування на сонці становить 3,9E-8 (0,000000039) . Це статистично значуще на рівні значущості 0,05.
• P-значення для взаємодії між частотою поливу та сонячним світлом становить 0,310898 . Це не є статистично значущим на рівні значущості 0,05.

Ці результати показують, що сонячне опромінення є єдиним фактором зі статистично значущим впливом на висоту рослин.

А оскільки немає ефекту взаємодії, вплив сонячного випромінювання є постійним на кожному рівні частоти поливу.

Простіше кажучи, те, щодня чи щотижня поливають рослину, не впливає на вплив сонця на рослину.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про моделі ANOVA:

Як інтерпретувати значення F і P у ANOVA
Як обчислити суму квадратів у ANOVA
Що означає високе значення F у ANOVA?