Як розрахувати p-значення в excel (3 приклади)

У статистиці ми використовуємо перевірку гіпотез , щоб визначити, чи є твердження про параметр сукупності істинним чи ні.

Коли ми виконуємо перевірку гіпотези, нам часто дають тестову статистику Т-балу.

Коли ми знайдемо цю статистику тесту t-показника, ми зможемо знайти пов’язане з нею значення p.

Якщо це p-значення менше певного значення (наприклад, 0,10, 0,05, 0,01), тоді ми відхиляємо нульову гіпотезу тесту та робимо висновок, що наші результати є статистично значущими.

У наведених нижче прикладах показано, як обчислити значення p для тестової статистики в Excel у трьох різних сценаріях.

Приклад 1: обчисліть значення P для двобічного тесту

Припустимо, ботанік хоче знати, чи дорівнює середня висота певного виду рослин 15 дюймам.

У випадковій вибірці з 12 рослин вона виявила, що середня висота зразка становить 14,33 дюйма, а стандартне відхилення зразка становить 1,37 дюйма.

Він виконує перевірку гіпотез, використовуючи такі нульові та альтернативні гіпотези:

H ₀ (нульова гіпотеза): μ= 15 дюймів

H _A (альтернативна гіпотеза): μ ≠ 15 дюймів

Статистика тесту розраховується наступним чином:

• t = ( X – µ) / (s/ √n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

Ступені свободи, пов’язані з цією тестовою статистикою, становлять n-1 = 12-1 = 11 .

Щоб знайти p-значення для цієї тестової статистики, ми скористаємося такою формулою в Excel:

 =T.DIST.2T(ABS(-1.694), 11)

На наступному знімку екрана показано, як використовувати цю формулу на практиці.

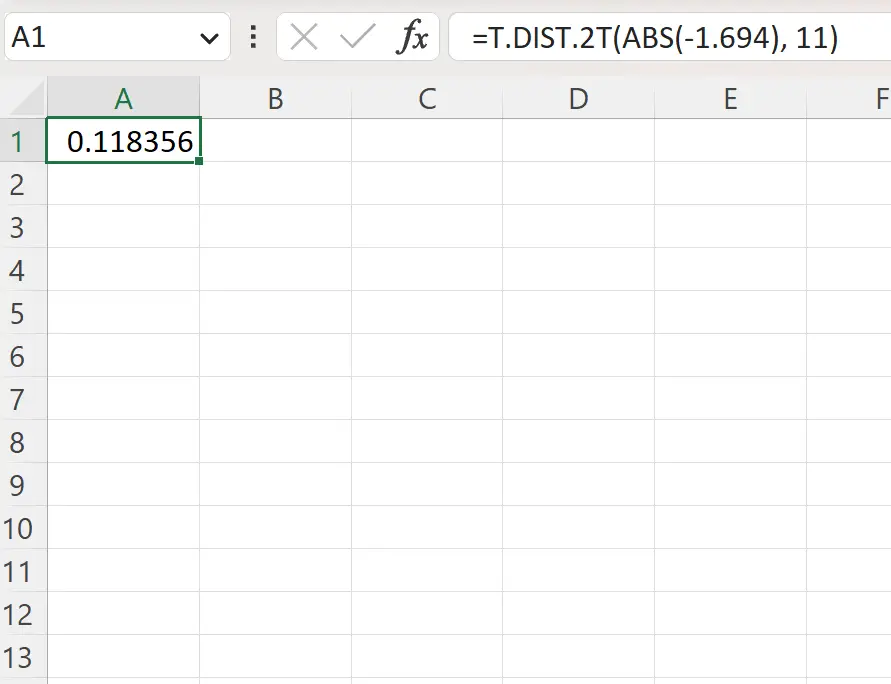
Двостороннє значення p становить 0,1184 .

Оскільки це значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. У нас немає достатньо доказів, щоб стверджувати, що середня висота рослини відрізняється від 15 дюймів.

Приклад 2: обчисліть значення P для тесту зліва

Припустимо, що середня вага певного гаджета, виготовленого на заводі, становить 20 грам. Однак інспектор оцінює реальну середню вагу менше 20 грамів.

Щоб перевірити це, він зважує просту випадкову вибірку з 20 віджетів і отримує таку інформацію:

• n = 20 віджетів
• х = 19,8 грам
• s = 3,1 грама

Потім виконується перевірка гіпотези, використовуючи такі нульові та альтернативні гіпотези:

H ₀ (нульова гіпотеза): μ ≥ 20 грам

H _A (альтернативна гіпотеза): μ < 20 грам

Статистика тесту розраховується наступним чином:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -,2885

Ступені свободи, пов’язані з цією тестовою статистикою, становлять n-1 = 20-1 = 19 .

Щоб знайти p-значення для цієї тестової статистики, ми скористаємося такою формулою в Excel:

 =T.DIST(-.2885, 19, TRUE)

На наступному знімку екрана показано, як використовувати цю формулу на практиці.

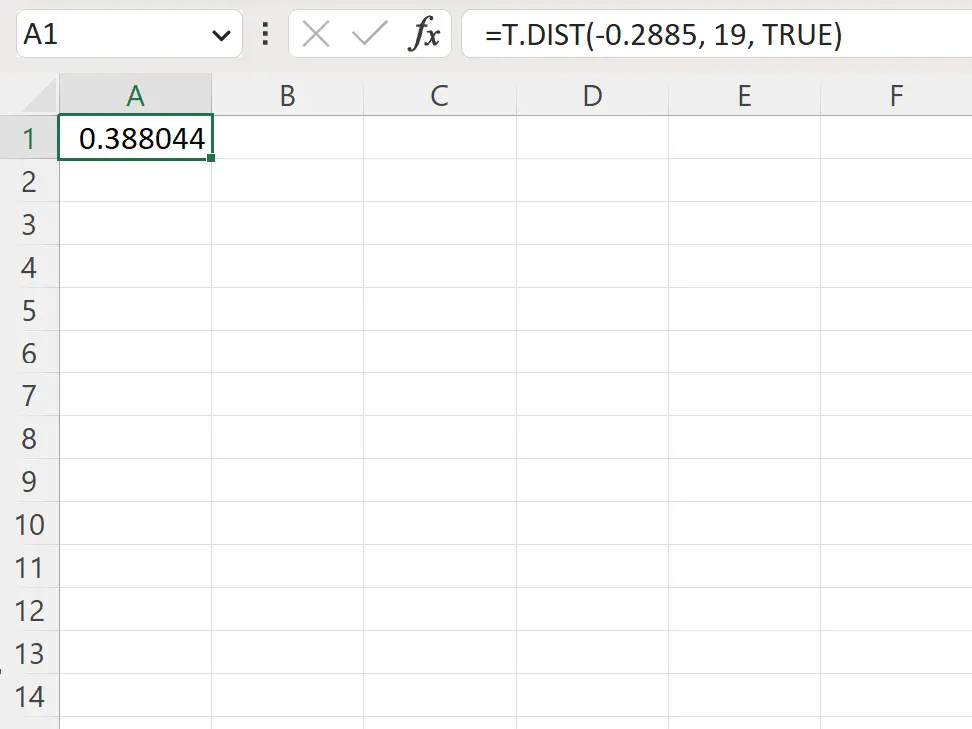
Р-значення ліворуч становить 0,388044 .

Оскільки це значення не менше 0,05, інспектор не відхиляє нульову гіпотезу. Немає достатніх доказів того, що фактична середня вага віджетів, вироблених на цій фабриці, становить менше 20 грамів.

Примітка . Ми використали аргумент TRUE , щоб вказати, що кумулятивну функцію розподілу слід використовувати під час обчислення p-значення.

Приклад 3: обчисліть значення P для тесту правого хвоста

Припустимо, що середня висота певного виду рослин становить 10 дюймів. Однак один ботанік каже, що справжня середня висота більше 10 дюймів.

Щоб перевірити це твердження, вона вимірює висоту простого випадкового зразка з 15 рослин і отримує таку інформацію:

• n = 15 рослин
• x = 11,4 дюйма
• s = 2,5 дюйма

Потім виконується перевірка гіпотези, використовуючи такі нульові та альтернативні гіпотези:

H ₀ (нульова гіпотеза): μ ≤ 10 дюймів

H _A (альтернативна гіпотеза): μ > 10 дюймів

Статистика тесту розраховується наступним чином:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Ступені свободи, пов’язані з цією тестовою статистикою, становлять n-1 = 15-1 = 14 .

Щоб знайти p-значення для цієї тестової статистики, ми скористаємося такою формулою в Excel:

 =T.DIST.RT(2.1689, 14)

На наступному знімку екрана показано, як використовувати цю формулу на практиці.

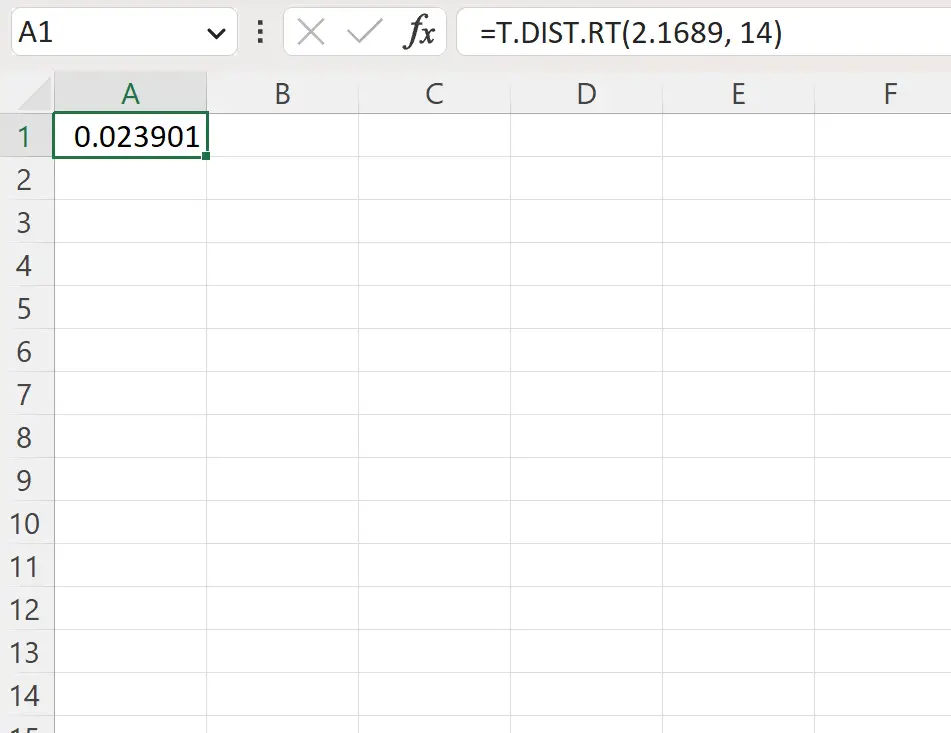
P-значення праворуч становить 0,023901 .

Якщо це значення менше 0,05, ботанік може відхилити нульову гіпотезу. Вона має достатньо доказів, щоб стверджувати, що справжня середня висота цього виду рослин перевищує 10 дюймів.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в Excel:

Як знайти значення P за шкалою Z в Excel
Як знайти значення P для F-статистики в Excel
Як знайти значення P статистики хі-квадрат в Excel