Односторонній дисперсійний аналіз: визначення, формула та приклад
Односторонній дисперсійний аналіз («дисперсійний аналіз») порівнює середні значення трьох або більше незалежних груп, щоб визначити, чи існує статистично значуща різниця між середніми значеннями відповідної сукупності.
Цей посібник пояснює наступне:
- Мотивація виконання одностороннього дисперсійного аналізу.
- Припущення, яких необхідно виконати для виконання одностороннього дисперсійного аналізу.
- Процес виконання одностороннього дисперсійного аналізу.
- Приклад того, як виконати односторонній дисперсійний аналіз.
Односторонній дисперсійний аналіз: мотивація
Припустімо, ми хочемо знати, чи призводять три різні програми підготовки до тестів до різних середніх балів на вступному іспиті до коледжу. Оскільки по всій країні є мільйони старшокласників, було б надто довго і дорого обійти кожного учня та дозволити йому скористатися однією з програм підготовки до іспиту.
Замість цього ми могли б вибрати три випадкові вибірки зі 100 студентів із сукупності та дозволити кожній вибірці використовувати одну з трьох програм підготовки до іспиту. Тоді ми могли б записати оцінки кожного студента після того, як він складе іспит.
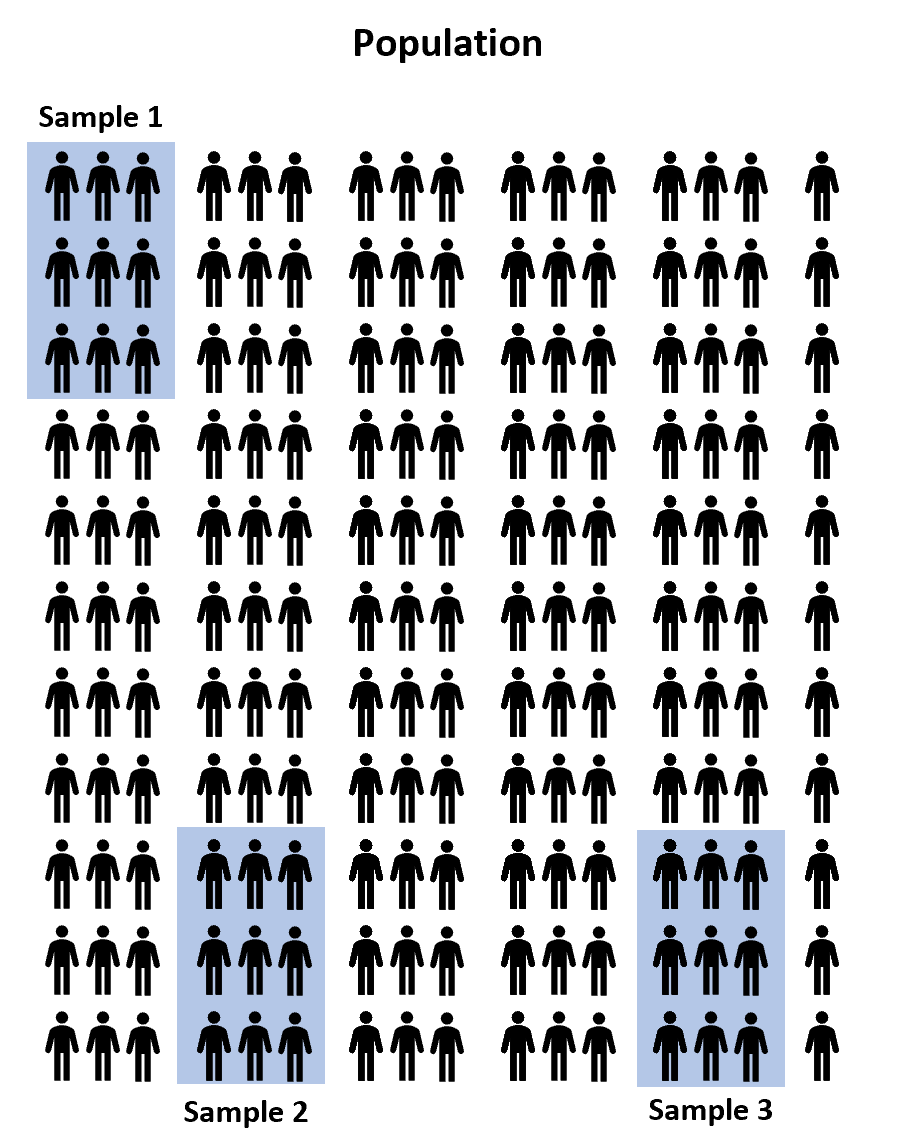
Однак практично гарантовано, що середній бал іспиту між трьома зразками буде принаймні трохи відрізнятися. Питання полягає в тому, чи ця різниця є статистично значущою . На щастя, односторонній ANOVA дозволяє нам відповісти на це запитання.
Односторонній дисперсійний аналіз: припущення
Щоб результати одностороннього дисперсійного аналізу були дійсними, мають бути виконані такі припущення:
1. Нормальність – кожен зразок був взятий із нормально розподіленої сукупності.
2. Рівні дисперсії – дисперсії популяцій, з яких відбираються зразки, рівні. Для перевірки цієї гіпотези можна використати критерій Бартлетта .
3. Незалежність – спостереження в кожній групі є незалежними одне від одного, а спостереження в групах були отримані шляхом випадкової вибірки.
Прочитайте цю статтю , щоб дізнатися більше про те, як перевірити ці припущення.
Односторонній дисперсійний аналіз: процес
Односторонній ANOVA використовує такі нульові та альтернативні гіпотези:
- H 0 (нульова гіпотеза): μ 1 = μ 2 = μ 3 = … = μ k (усі середні сукупності рівні)
- H 1 (альтернативна гіпотеза): принаймні одне середнє значення сукупності відрізняється відпочинок
Зазвичай ви використовуєте якесь статистичне програмне забезпечення (наприклад, R, Excel, Stata, SPSS тощо) для виконання одностороннього дисперсійного аналізу, оскільки це втомливо виконувати вручну.
Незалежно від програмного забезпечення, яке ви використовуєте, ви отримаєте таку таблицю як вихідні дані:
| Джерело | Сума квадратів (SS) | df | Середні квадрати (MS) | Ф | стор |
|---|---|---|---|---|---|
| Лікування | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Помилка | ESS | df e | MSE | ||
| Всього | OHS | df t |
золото:
- SSR: регресія суми квадратів
- SSE: сума квадратів помилок
- SST: загальна сума квадратів (SST = SSR + SSE)
- df r : регресійні ступені свободи (df r = k-1)
- df e : похибка ступенів свободи (df e = nk)
- df t : загальна кількість ступенів свободи (df t = n-1)
- k: загальна кількість груп
- n: загальна кількість спостережень
- MSR: середньоквадратична регресія (MSR = SSR/df r )
- MSE: середня квадратична помилка (MSE = SSE/df e )
- F: Статистика тесту F (F = MSR/MSE)
- p: значення p, яке відповідає F dfr, dfe
Якщо p-значення менше вибраного рівня значущості (наприклад, 0,05), ви можете відхилити нульову гіпотезу та зробити висновок, що принаймні одне із середніх сукупностей відрізняється від інших.
Примітка. Якщо ви відхиляєте нульову гіпотезу, це вказує на те, що принаймні одне із середніх сукупностей відрізняється від інших, але таблиця ANOVA не вказує , які середні сукупності відрізняються. Щоб визначити це, вам потрібно виконати пост-хок тестування , яке також називають тестуванням «множинного порівняння».
Односторонній дисперсійний аналіз: приклад
Припустімо, ми хочемо знати, чи три різні програми підготовки до іспиту призводять до різних середніх балів на даному іспиті. Щоб перевірити це, ми набираємо 30 студентів для участі в дослідженні та ділимо їх на три групи.
Студенти в кожній групі випадковим чином розподіляються для використання однієї з трьох програм підготовки до іспиту протягом наступних трьох тижнів для підготовки до іспиту. Після закінчення трьох тижнів усі студенти складають один і той же іспит.
Результати іспитів для кожної групи наведені нижче:

Щоб виконати односторонній дисперсійний аналіз цих даних, ми використаємо статистичний односторонній калькулятор дисперсійного аналізу з такими вхідними даними:

З вихідної таблиці ми бачимо, що статистика F-тесту становить 2,358 , а відповідне значення p — 0,11385 .

Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.
Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що існує статистично значуща різниця між середніми іспитовими балами трьох груп.
Додаткові ресурси
У наступних статтях пояснюється, як виконати односторонній дисперсійний аналіз за допомогою різного статистичного програмного забезпечення:
Як виконати односторонній дисперсійний аналіз в Excel
Як виконати односторонній дисперсійний аналіз у R
Як виконати односторонній дисперсійний аналіз у Python
Як виконати односторонній дисперсійний аналіз у SAS
Як виконати односторонній дисперсійний аналіз у SPSS
Як виконати односторонній дисперсійний аналіз у Stata
Як виконати односторонній дисперсійний аналіз на калькуляторі TI-84
Онлайн-калькулятор одностороннього дисперсійного аналізу