Як виконати односторонній дисперсійний аналіз в excel

Односторонній дисперсійний аналіз («дисперсійний аналіз») використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

У цьому посібнику пояснюється, як виконати односторонній дисперсійний аналіз у Excel.

Приклад: односторонній дисперсійний аналіз у Excel

Припустімо, що дослідник набирає 30 студентів для участі в дослідженні. Студенти випадковим чином розподіляються для використання однієї з трьох методів навчання протягом наступних трьох тижнів для підготовки до іспиту. Наприкінці трьох тижнів усі учні складають той самий тест.

Результати тестування студентів наведено нижче:

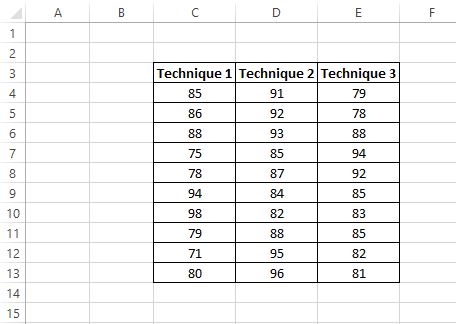
Дослідник хоче виконати односторонній дисперсійний аналіз, щоб визначити, чи однакові середні бали в трьох групах.

Щоб виконати односторонній дисперсійний аналіз в Excel, перейдіть на вкладку «Дані» , а потім клацніть параметр «Аналіз даних» у групі «Аналіз» .

Якщо ви не бачите опцію «Аналіз даних » , спочатку потрібно завантажити безкоштовне програмне забезпечення Analysis ToolPak .

Коли ви клацнете на ньому, з’явиться вікно з різними параметрами інструмента сканування. Виберіть Anova: Single Factor і натисніть OK .

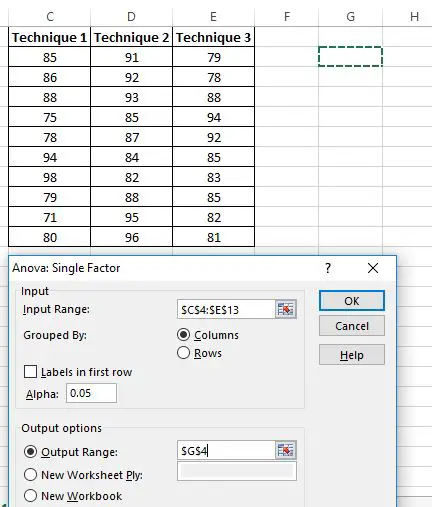
З’явиться нове вікно із запитом на введення діапазону . Ви можете перетягнути рамку навколо своїх даних або вручну ввести діапазон даних. У цьому випадку наші дані знаходяться в клітинках C4:E13 .

Далі виберіть рівень альфа для тесту. За замовчуванням це число дорівнює 0,05. У цьому випадку я залишу його на рівні 0,05.

Нарешті виберіть комірку для діапазону вихідних даних , де відображатимуться результати одностороннього дисперсійного аналізу. У цьому випадку я вибираю клітинку G4 .

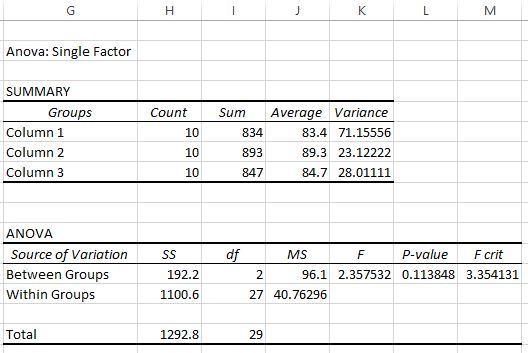
Після натискання кнопки OK з’явиться односторонній результат ANOVA:

Інтерпретація результату

У вихідних даних відображаються дві таблиці. Перший — підсумкова таблиця, яка показує кількість тестових балів у кожній групі, суму тестових балів, середнє значення тестових балів і дисперсію тестових балів.

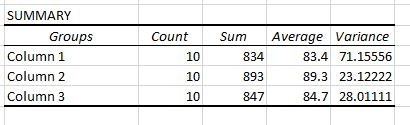
Нагадаємо, що односторонній дисперсійний аналіз використовується для визначення того, чи існує статистично значуща різниця між середніми значеннями трьох або більше груп.

З цієї першої таблиці ми бачимо, що середній бал для кожної з трьох груп відрізняється, але щоб дізнатися, чи є ці відмінності статистично значущими, нам потрібно поглянути на другу таблицю.

Друга таблиця показує статистику тесту F, критичне значення F і значення p:

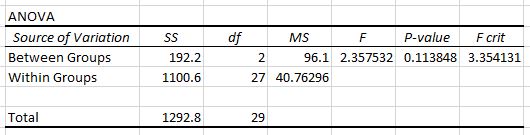
У цьому випадку статистика F-тесту становить 2,3575 , а критичне значення F — 3,3541 . Оскільки статистика тесту F менша за критичне значення F, ми не маємо достатніх доказів, щоб відхилити нульову гіпотезу про те, що середні значення трьох груп рівні.

Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що існує різниця в результатах тестування між трьома методами дослідження.

Ми також можемо використати p-значення , щоб дійти того самого висновку. У цьому випадку p-значення становить 0,1138 , що вище, ніж рівень альфа 0,05 .

Це означає, що ми не маємо достатніх доказів, щоб відхилити нульову гіпотезу про те, що середні три групи рівні.

Примітка. У випадках, коли ви відхиляєте нульову гіпотезу, ви можете виконати тест Тьюкі-Крамера, щоб точно визначити, які групові середні відрізняються.