Що таке бал станіна? (визначення та приклади)
Оцінка Станіна , скорочення від «стандартної оцінки дев’ять», — це спосіб шкалювання результатів тесту за стандартною дев’ятибальною шкалою.
Використовуючи цей метод, ми можемо конвертувати кожен результат тесту з початкового балу (тобто від 0 до 100) на число від 1 до 9.
Ми використовуємо простий двоетапний процес, щоб адаптувати результати тесту до балів Станіна:
1. Розташуйте кожен результат тесту від найнижчого до найвищого.
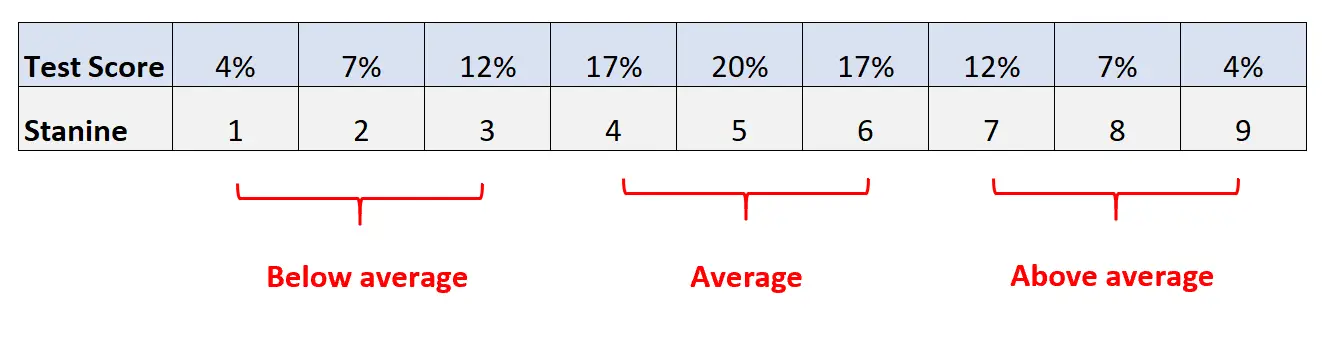
2. Дайте найнижчим 4% балів оцінку за Станіном 1, наступним найнижчим 7% оцінок оцінку за Станіном 2 і так далі відповідно до наступної таблиці:

Загалом ми розглядаємо результати тестування наступним чином:
- Станіни 1, 2, 3: нижче середнього
- Станіни 4, 5, 6: Середнє
- Станіни 7, 8, 9: вище середнього
Виявляється, що шкала Станіна має середнє значення п’ять і стандартне відхилення два.
Переваги та недоліки оцінки Stanine
Оцінка Станіна має такі переваги та недоліки:
Переваги: Оцінки за Станіном дозволяють нам швидко зрозуміти, яке місце займає даний тестовий бал по відношенню до всіх інших результатів тестування.
Наприклад, ми знаємо, що студент із тестовим балом Stanine 5 знаходиться в середині 20% усіх тестових балів. І ми знаємо, що у студента, який впав на станін 9, тестовий результат увійшов до 4% найкращих балів.
Недолік. Недоліком використання станінів є те, що кожен станін не має однакового розміру, і тестовий бал у даному станіні може бути ближчим до балів наступного станіну порівняно з балами його власного станіну.
Наприклад, усі студенти, які мають результати між 40-м і 60-м процентилем, групуються до рівня 5. Проте студент, чий тестовий результат знаходиться на 58-му процентилі, буде ближчим до результатів, отриманих на рівні 6, ніж більшість балів. отримано в станині 5.
Альтернативи оцінки Станіна
Двома альтернативами показникам Станіна є процентилі та z-рахунки.
1. Процентиль говорить нам про відсоток усіх балів, вище якого падає даний тестовий бал.
Наприклад, 90-й процентиль перевищує 90% результатів усіх тестів. Тестовий результат, який знаходиться на 50-му процентилі, знаходиться точно посередині всіх тестових балів.
2. Z-показник повідомляє нам, скільки стандартних відхилень даний показник має від середнього. Він розраховується таким чином:
z = (X – μ) / σ
золото:
- X – це одне значення необроблених даних
- μ — середнє значення набору даних
- σ — стандартне відхилення набору даних
Ми інтерпретуємо z-показники наступним чином:
- Позитивна z-оцінка означає, що тестова оцінка вище середнього
- Негативний z-бал означає, що тестовий бал нижчий за середній
- Нульовий показник z означає, що результат тесту точно дорівнює середньому значенню
Чим далі z-оцінка від нуля, тим далі заданий тестовий бал від середнього.
Z-оцінки та процентилі дають нам більш точне уявлення про ранг певних тестових балів порівняно з балами Станіна.