Як виконати поліноміальну регресію в python

Регресійний аналіз використовується для кількісного визначення зв’язку між однією або декількома пояснювальними змінними та змінною відповіді.

Найпоширенішим типом регресійного аналізу є проста лінійна регресія , яка використовується, коли прогностична змінна та змінна відповіді мають лінійний зв’язок.

Однак інколи зв’язок між змінною-прогнозом і змінною відповіді є нелінійним.

Наприклад, справжня залежність може бути квадратичною:

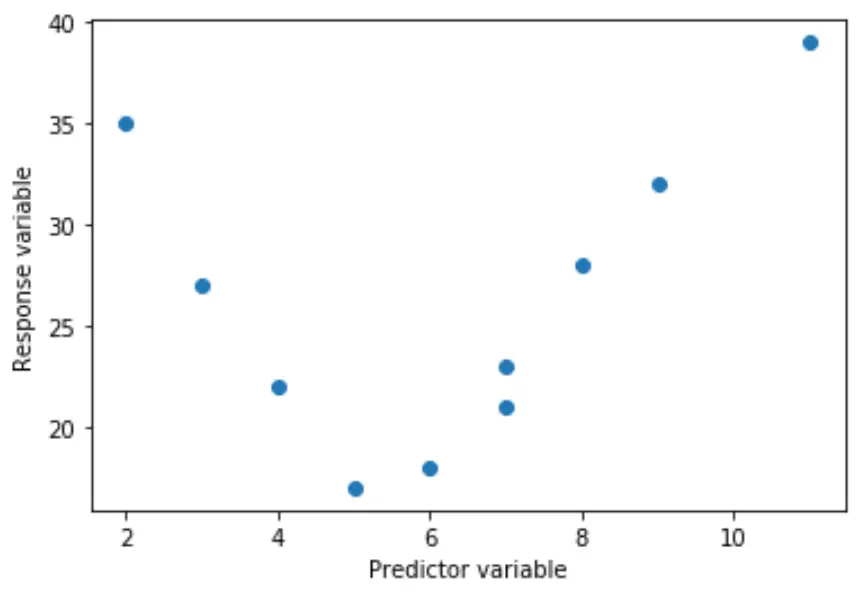
Або він може бути кубічним:

У цих випадках має сенс використовувати поліноміальну регресію , яка може врахувати нелінійний зв’язок між змінними.

Цей посібник пояснює, як виконувати поліноміальну регресію в Python.

Приклад: поліноміальна регресія в Python

Припустімо, що ми маємо наступну змінну предиктора (x) і змінну відповіді (y) у Python:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Якщо ми створимо просту діаграму розсіювання цих даних, ми побачимо, що зв’язок між x і y явно не лінійний:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

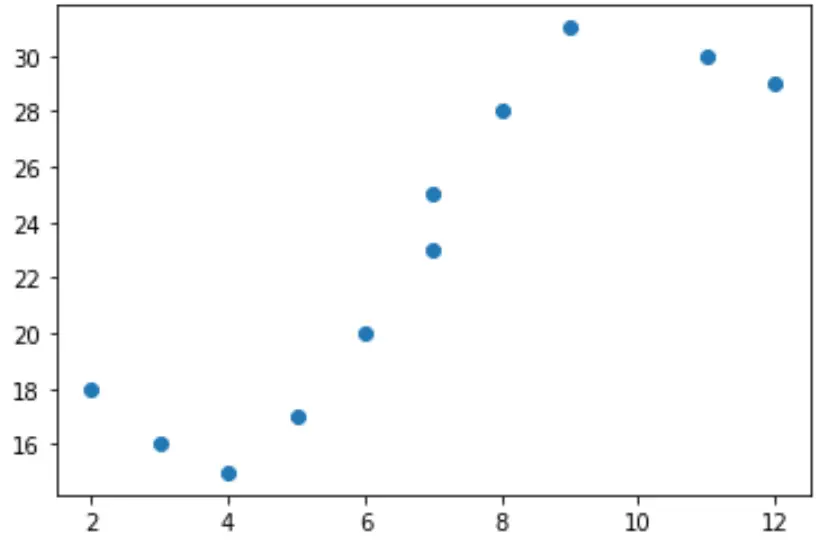
Тому не має сенсу пристосовувати модель лінійної регресії до цих даних. Замість цього ми можемо спробувати підібрати модель поліноміальної регресії зі ступенем 3 за допомогою функції numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

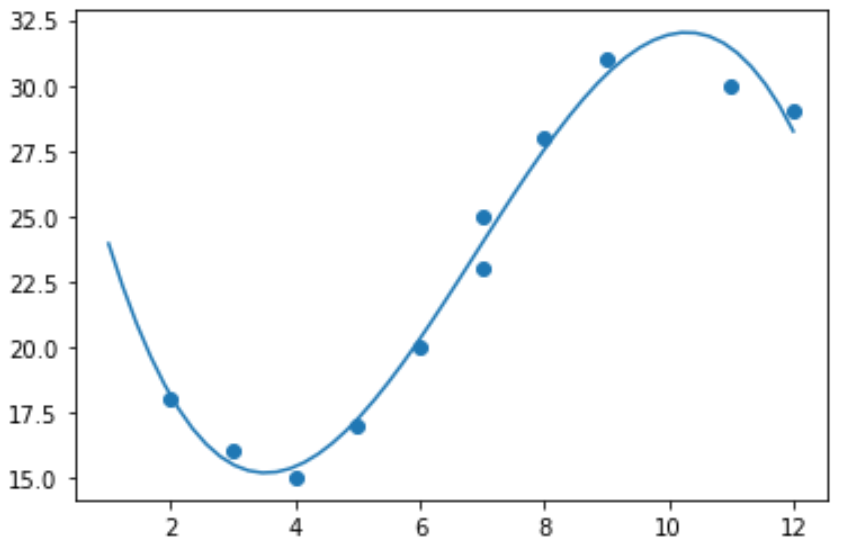
Ми можемо отримати підігнане поліноміальне рівняння регресії, надрукувавши коефіцієнти моделі:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

Підігнане рівняння поліноміальної регресії має вигляд:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Це рівняння можна використовувати для знаходження очікуваного значення змінної відповіді за даного значення пояснювальної змінної.

Наприклад, припустимо, що x = 4. Очікуване значення для змінної відповіді, y, буде:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Ми також можемо написати коротку функцію, щоб отримати R-квадрат моделі, який є часткою дисперсії у змінній відповіді, яку можна пояснити змінними предиктора.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

У цьому прикладі R-квадрат моделі становить 0,9841 .

Це означає, що 98,41% варіації змінної відповіді можна пояснити змінними предикторами.