Як виконати поліноміальну регресію за допомогою scikit-learn

Поліноміальна регресія — це техніка, яку ми можемо використовувати, коли зв’язок між змінною предиктором і змінною відповіді нелінійний.

Цей тип регресії має вигляд:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

де h – «ступінь» полінома.

Наступний покроковий приклад показує, як виконати поліноміальну регресію в Python за допомогою sklearn.

Крок 1: Створіть дані

Спочатку давайте створимо два масиви NumPy для зберігання значень предиктора та змінної відповіді:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

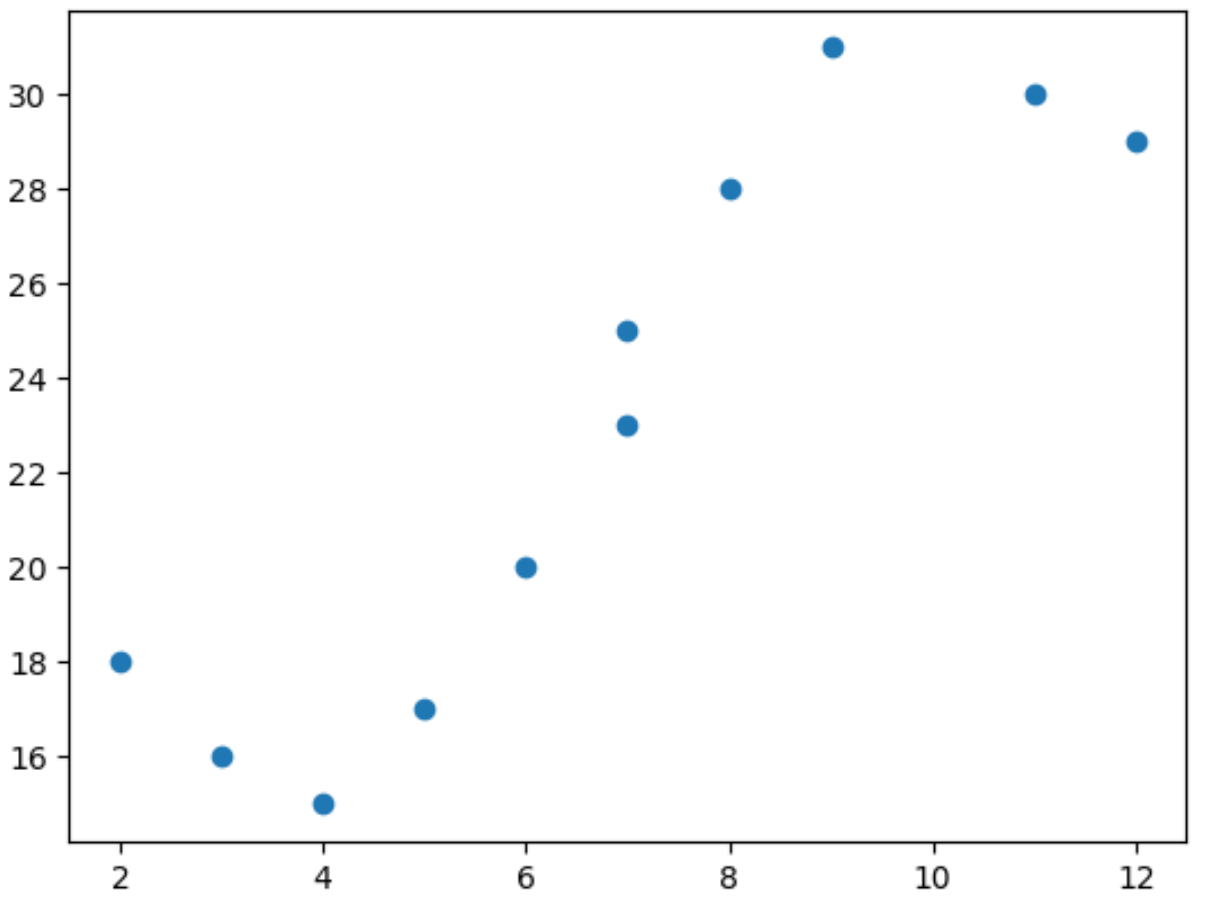
З діаграми розсіювання ми бачимо, що залежність між x і y не є лінійною.

Тому гарною ідеєю буде підібрати модель поліноміальної регресії до даних, щоб охопити нелінійний зв’язок між двома змінними.

Крок 2. Підберіть модель поліноміальної регресії

У наведеному нижче коді показано, як використовувати функції sklearn для підгонки моделі поліноміальної регресії третього ступеня до цього набору даних:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Використовуючи коефіцієнти моделі, показані в останньому рядку, ми можемо записати підібране рівняння поліноміальної регресії таким чином:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Це рівняння можна використовувати для знаходження очікуваного значення змінної відповіді за даного значення прогнозованої змінної.

Наприклад, якщо x дорівнює 4, очікуване значення для змінної відповіді y буде 15,39:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Примітка . Щоб відповідати моделі поліноміальної регресії з іншим ступенем, просто змініть значення аргументу ступеня у функції PolynomialFeatures() .

Крок 3: Візуалізуйте модель поліноміальної регресії

Нарешті, ми можемо створити простий графік для візуалізації моделі поліноміальної регресії, підігнаної до вихідних точок даних:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

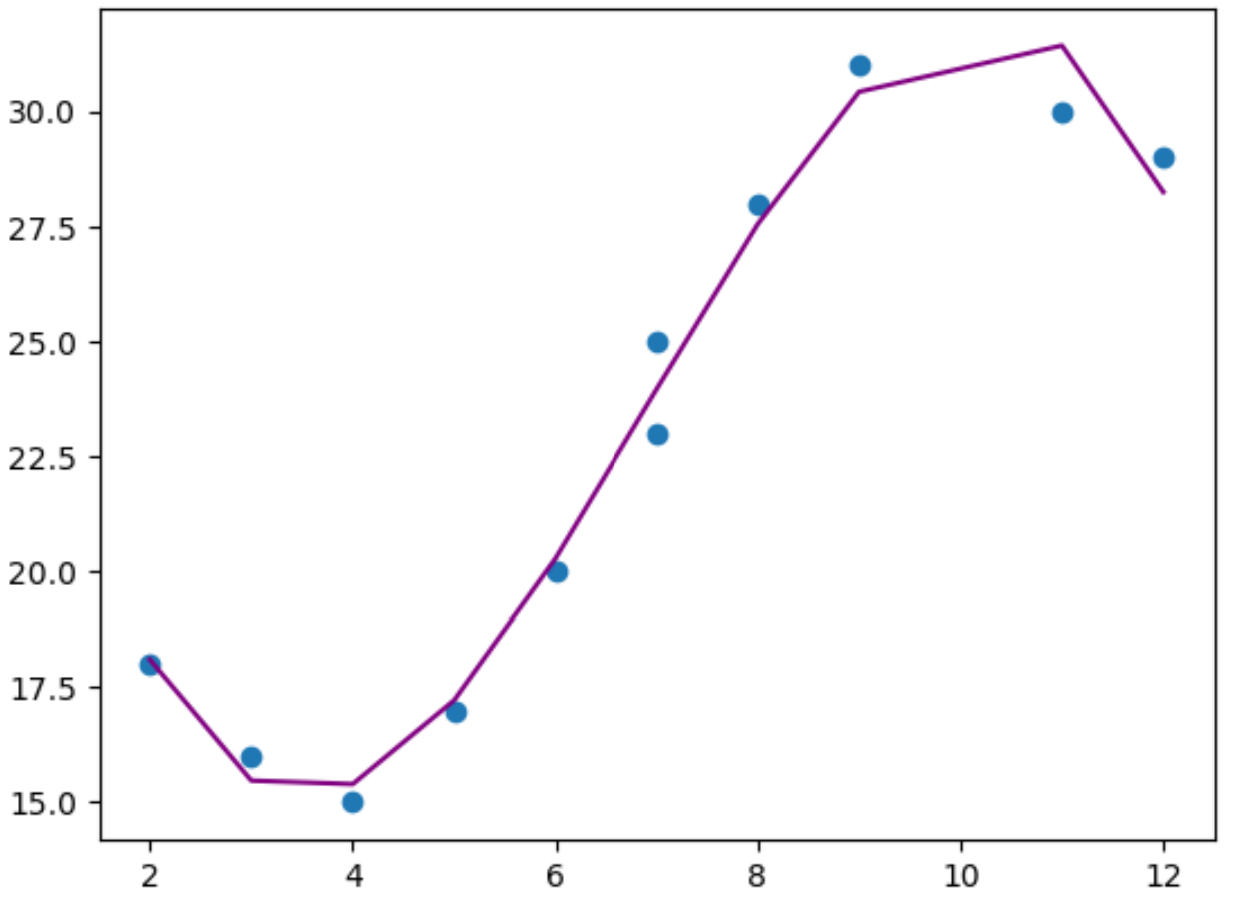
З графіка ми бачимо, що поліноміальна регресійна модель добре відповідає даним без переобладнання .

Примітка . Ви можете знайти повну документацію для функції sklearn PolynomialFeatures() тут .

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання за допомогою sklearn:

Як отримати коефіцієнти регресії з sklearn
Як розрахувати збалансовану точність за допомогою sklearn
Як інтерпретувати класифікаційний звіт у Sklearn