Як порівняти діаграми коробок: із прикладами

Ящичний графік – це тип графіка, який відображає п’ятизначний підсумок набору даних, який включає:

• Мінімальне значення
• Перший квартиль (25-й процентиль)
• Середнє значення
• Третій квартиль (75-й процентиль)
• Максимальне значення

Щоб зробити прямокутний графік, ми малюємо прямокутник від першого до третього квартиля. Далі проводимо вертикальну лінію по середині. Нарешті, малюємо «вуса» квартилів до мінімального та максимального значення.

Коробкові діаграми корисні, оскільки вони дозволяють нам швидко зрозуміти розподіл значень у наборі даних. Вони також корисні для порівняння двох різних наборів даних.

Порівнюючи дві або більше коробкових діаграм, ми можемо відповісти на чотири різні запитання:

1. Як порівнюють медіанні значення? Ми можемо порівняти вертикальну лінію в кожному полі, щоб визначити, який набір даних має вище середнє значення.

2. Як порівняти дисперсію? Ми можемо порівняти довжину кожного прямокутника (що представляє відстань між Q1 і Q3 – інтерквартильний діапазон), щоб визначити, який набір даних більший.

3. Як порівнюється асиметрія? Чим ближче вертикальна лінія до першого кварталу, тим більше спотворений набір даних. Чим ближче вертикальна лінія до третього кварталу, тим більше спотворений набір даних.

4. Чи присутні викиди? На прямокутних діаграмах викиди зазвичай представлені крихітними колами, які виходять за межі кожного вуса. Спостереження визначається як викид, якщо воно відповідає одному з наступних критеріїв:

• Одне спостереження менше Q1 – 1,5*IQR
• Спостереження перевищує Q3 + 1,5*IQR

У наступному прикладі показано, як порівняти два різні коробкові графіки та відповісти на ці чотири запитання.

Приклад: порівняння діаграм в коробці

Наступні набори даних відображають результати студентів, які використовували один із двох методів навчання для підготовки до іспиту:

Спосіб 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Спосіб 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Якщо ми створимо коробкові діаграми для кожного набору даних, вони виглядатимуть ось як:

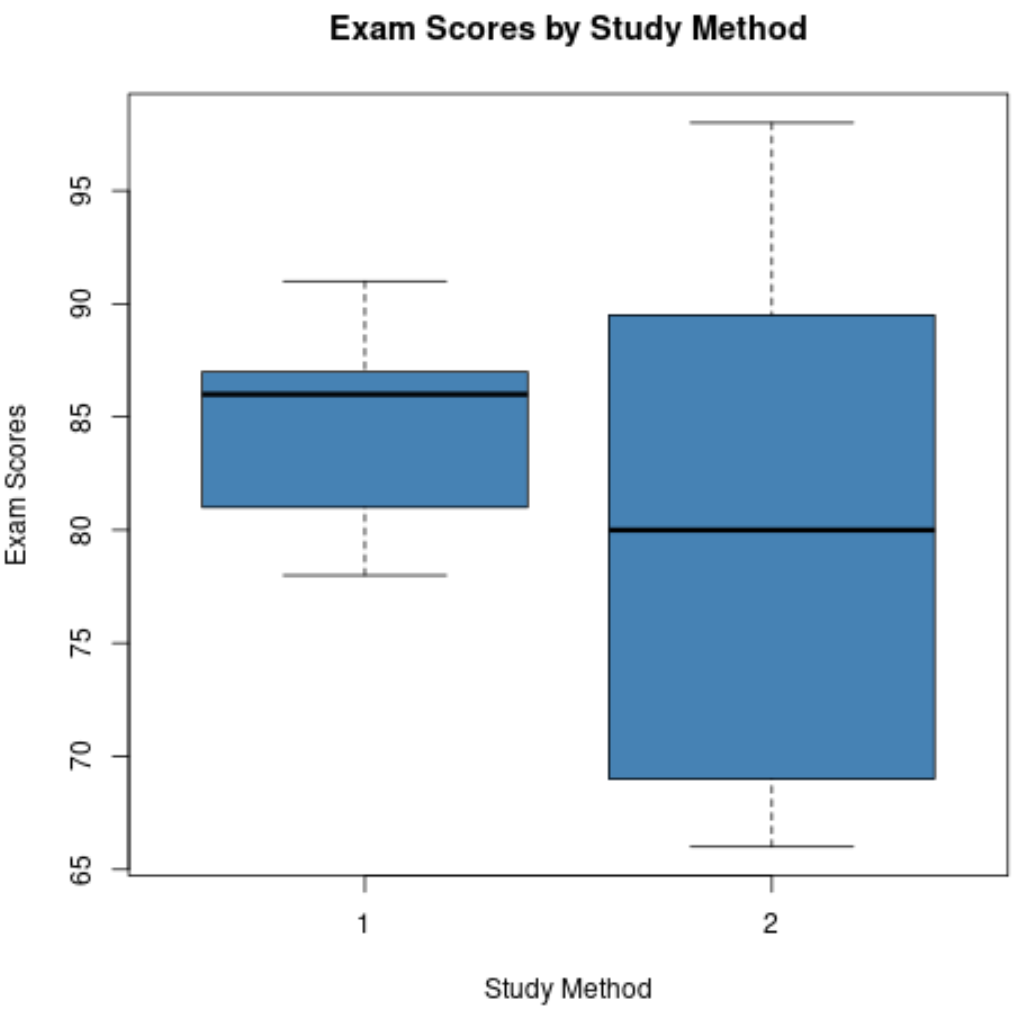
Ми можемо порівняти ці дві коробкові діаграми та відповісти на такі чотири запитання:

1. Як порівнюють медіанні значення? Лінія в середині прямокутної діаграми для методу навчання 1 вища за лінію для методу навчання 2, що вказує на те, що студенти, які використовували метод навчання 1, мали середню оцінку на вищому іспиті.

2. Як порівняти дисперсію? Коробковий графік для методу навчання 2 набагато довший, ніж для методу навчання 1, що вказує на те, що бали за іспит набагато більше розподіляються серед студентів, які використовували метод навчання 2.

3. Як порівнюється асиметрія? Лінія в середині прямокутної діаграми для методу навчання 1 близька до Q3, що вказує на те, що розподіл іспитових балів для студентів, які використовували метод навчання 1, має негативний перекіс. І навпаки, лінія в середині прямокутної діаграми для методу дослідження 2 розташована близько до центру прямокутника, що означає, що розподіл балів є мінімально спотвореним.

4. Чи присутні викиди? Жодна коробкова графіка не має крихітних кіл, які виходять за межі верхнього чи нижнього вусів, що означає, що жоден набір даних не має чітких викидів.

Додаткові ресурси

Як створити та інтерпретувати діаграми коробок у Excel
Як створити та інтерпретувати коробкові діаграми в SPSS
Як створити кілька діаграм в R
Як створювати та інтерпретувати коробкові діаграми в Stata