Чотири припущення лінійної регресії

Лінійна регресія є корисним статистичним методом, який ми можемо використовувати для розуміння зв’язку між двома змінними, x і y. Однак перш ніж виконувати лінійну регресію, ми повинні переконатися, що виконуються чотири припущення:

1. Лінійний зв’язок: існує лінійний зв’язок між незалежною змінною x і залежною змінною y.

2. Незалежність: Залишки є незалежними. Зокрема, немає кореляції між послідовними залишками в даних часових рядів.

3. Гомоскедастичність: залишки мають постійну дисперсію на кожному рівні x.

4. Нормальність: модельні залишки розподілені нормально.

Якщо одне або декілька з цих припущень не виконуються, то результати нашої лінійної регресії можуть бути ненадійними або навіть оманливими.

У цій статті ми надаємо пояснення для кожного припущення, як визначити, чи виконується припущення, і що робити, якщо припущення не виконується.

Гіпотеза 1: Лінійний зв’язок

Пояснення

Перше припущення лінійної регресії полягає в тому, що між незалежною змінною x і незалежною змінною y існує лінійна залежність.

Як визначити, чи виконується це припущення

Найпростіший спосіб визначити, чи виконується це припущення, — створити діаграму розсіювання x проти y. Це дозволяє візуально побачити, чи існує лінійна залежність між двома змінними. Якщо здається, що точки на графіку можуть лежати вздовж прямої лінії, то між двома змінними існує якийсь тип лінійного зв’язку, і це припущення виконується.

Наприклад, точки на наведеному нижче графіку виходять на пряму лінію, що вказує на те, що існує лінійна залежність між x і y:

Однак на наведеному нижче графіку немає лінійного зв’язку між x і y:

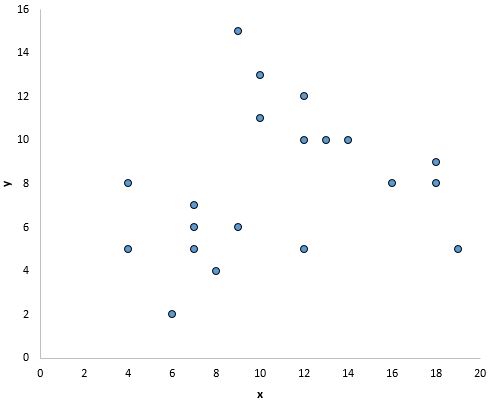
І на цьому графіку, здається, існує чіткий зв’язок між x і y, але не лінійний зв’язок :

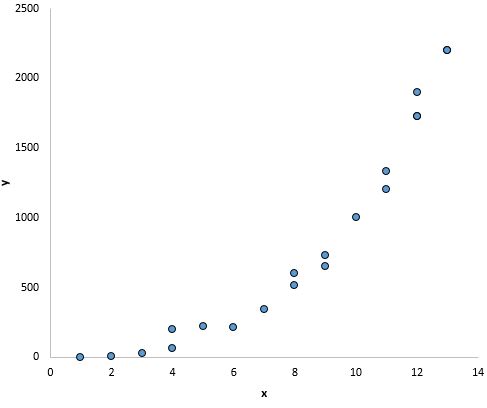
Що робити, якщо це припущення не виконується

Якщо ви створюєте діаграму розсіювання значень для x і y і виявите, що між двома змінними немає лінійного зв’язку, у вас є кілька варіантів:

1. Застосуйте нелінійне перетворення до незалежної та/або залежної змінної. Типові приклади включають логарифм, квадратний корінь або зворотну величину незалежної та/або залежної змінної.

2. Додайте до моделі іншу незалежну змінну. Наприклад, якщо графік залежності x від y має параболічну форму, може мати сенс додати X ² як додаткову незалежну змінну в модель.

Гіпотеза 2: Незалежність

Пояснення

Наступне припущення лінійної регресії полягає в тому, що залишки є незалежними. Це особливо актуально при роботі з даними часових рядів. В ідеалі ми не хочемо, щоб була тенденція серед послідовних залишків. Наприклад, залишки не повинні постійно збільшуватися з часом.

Як визначити, чи виконується це припущення

Найпростіший спосіб перевірити, чи справджується це припущення, — подивитися на графік часових рядів залишків, який є графіком залежності залишків від часу. В ідеалі більшість залишкових автокореляцій повинні знаходитися в межах 95% довірчих діапазонів навколо нуля, які розташовані приблизно +/- 2 від квадратного кореня з n , де n – розмір вибірки. Ви також можете формально перевірити, чи виконується це припущення, використовуючи тест Дарбіна-Ватсона .

Що робити, якщо це припущення не виконується

Залежно від того, як це припущення порушено, у вас є кілька варіантів:

• Для позитивної послідовної кореляції розгляньте можливість додавання лагів залежної та/або незалежної змінної до моделі.
• Для негативної послідовної кореляції переконайтеся, що жодна з ваших змінних не має надмірної затримки .
• Для сезонної кореляції розгляньте можливість додавання сезонних фіктивних елементів до моделі.

Гіпотеза 3: гомоскедастичність

Пояснення

Наступне припущення лінійної регресії полягає в тому, що залишки мають постійну дисперсію на кожному рівні x. Це називається гомоскедастичністю . Коли це не так, залишки страждають від гетероскедастичності .

Коли гетероскедастичність присутня в регресійному аналізі, у результати аналізу стає важко повірити. Зокрема, гетероскедастичність збільшує дисперсію оцінок коефіцієнта регресії, але регресійна модель не враховує це. Це значно підвищує ймовірність того, що регресійна модель стверджуватиме, що термін у моделі є статистично значущим, хоча насправді це не так.

Як визначити, чи виконується це припущення

Найпростіший спосіб виявити гетероскедастичність – це створити підігнаний графік значення/залишок .

Після підгонки лінії регресії до набору даних можна створити діаграму розсіювання, яка показує підібрані значення моделі проти залишків цих підігнаних значень. Діаграма розсіювання нижче показує типовий графік підігнаного значення проти залишку, в якому присутня гетероскедастичність.

Зверніть увагу, як залишки розповсюджуються все більше і більше в міру збільшення підігнаних значень. Ця форма «конуса» є класичною ознакою гетероскедастичності:

Що робити, якщо це припущення не виконується

Існує три поширених способи корекції гетероскедастичності:

1. Перетворення залежної змінної. Звичайним перетворенням є просто взяття журналу залежної змінної. Наприклад, якщо ми використовуємо чисельність населення (незалежну змінну), щоб передбачити кількість флористів у місті (залежна змінна), натомість ми можемо спробувати використати чисельність населення, щоб передбачити логарифм кількості флористів у місті. Використання логарифму залежної змінної, а не початкової залежної змінної, часто призводить до зникнення гетероскедастичності.

2. Перевизначте залежну змінну. Поширеним способом перевизначення залежної змінної є використання швидкості , а не вихідного значення. Наприклад, замість того, щоб використовувати чисельність населення для прогнозування кількості флористів у місті, ми можемо використовувати чисельність населення для прогнозування кількості флористів на душу населення. У більшості випадків це зменшує мінливість, яка природно виникає у великих популяціях, оскільки ми вимірюємо кількість флористів на людину, а не саму кількість флористів.

3. Використовуйте зважену регресію. Іншим способом виправлення гетероскедастичності є використання зваженої регресії. Цей тип регресії призначає вагу кожній точці даних на основі дисперсії її підігнаного значення. По суті, це дає низькі ваги точкам даних, які мають більшу дисперсію, зменшуючи їхні залишкові квадрати. Якщо використовуються відповідні ваги, це може усунути проблему гетероскедастичності.

Гіпотеза 4: нормальність

Пояснення

Наступне припущення лінійної регресії полягає в тому, що залишки розподілені нормально.

Як визначити, чи виконується це припущення

Є два поширених способи перевірити, чи виконується це припущення:

1. Візуально перевірте гіпотезу за допомогою графіків QQ .

Діаграма QQ, скорочення від quantile-quantile plot, — це тип графіка, за допомогою якого ми можемо визначити, чи відповідають залишки моделі нормальному розподілу. Якщо точки на графіку приблизно утворюють пряму діагональну лінію, тоді виконується припущення про нормальність.

Наступний графік QQ показує приклад залишків, які приблизно відповідають нормальному розподілу:

Однак наведений нижче графік QQ показує приклад випадку, коли залишки чітко відхиляються від прямої діагональної лінії, що вказує на те, що вони не відповідають нормальному розподілу:

2. Ви також можете перевірити припущення про нормальність за допомогою формальних статистичних тестів, таких як Шапіро-Вілка, Колмогорова-Смиронова, Жарка-Барре або Д’Агостіно-Пірсона. Однак майте на увазі, що ці тести чутливі до великих розмірів вибірки, тобто вони часто роблять висновок, що залишки не є нормальними, коли розмір вашої вибірки великий. Ось чому для перевірки цієї гіпотези часто простіше просто використовувати графічні методи, такі як графік QQ.

Що робити, якщо це припущення не виконується

Якщо припущення про нормальність не виконується, у вас є кілька варіантів:

• Спочатку переконайтеся, що викиди не мають великого впливу на розподіл. Якщо є викиди, переконайтеся, що це реальні значення, а не помилки введення даних.
• Потім ви можете застосувати нелінійне перетворення до незалежної та/або залежної змінної. Типові приклади включають логарифм, квадратний корінь або зворотну величину незалежної та/або залежної змінної.

Подальше читання:

Вступ до простої лінійної регресії
Розуміння гетероскедастичності в регресійному аналізі
Як створити та інтерпретувати діаграму QQ у R