Чи передбачає причинно-наслідковий зв’язок кореляцію? (3 приклади)

Добре відомо, що кореляція не передбачає причинно-наслідкового зв’язку .

Як простий приклад, якщо ми щорічно збираємо дані про загальну кількість випускників середньої школи та загальне споживання піци в Сполучених Штатах, ми виявимо, що ці дві змінні сильно корелюють:

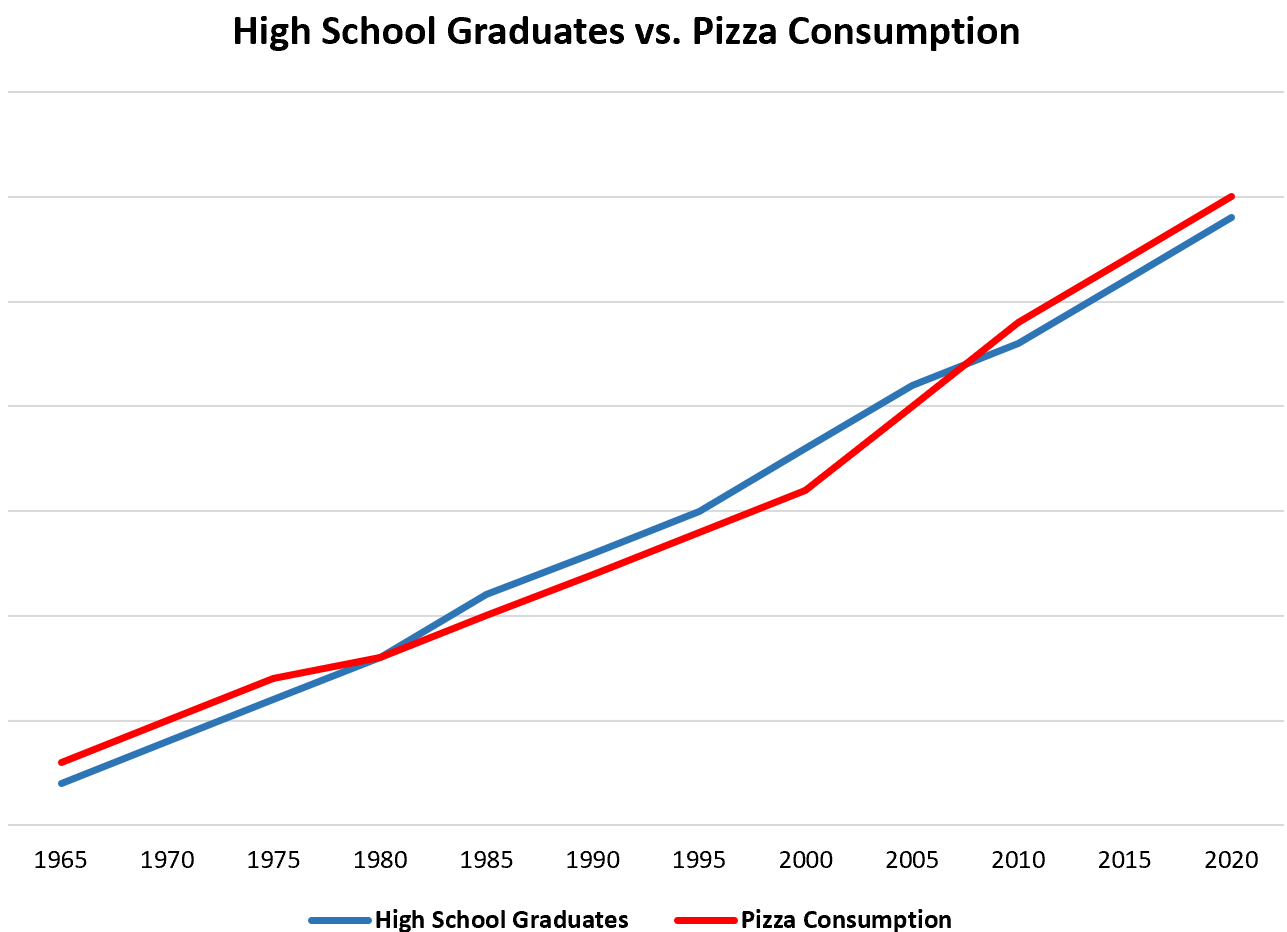
Це не означає, що збільшення кількості випускників веде до зростання споживання піци.

Найбільш імовірним поясненням є те, що населення США з часом зросло, тобто кількість людей із дипломом про середню освіту та загальна кількість спожитої піци зростає зі збільшенням населення.

Але як щодо протилежного твердження: чи передбачає причинно-наслідковий зв’язок кореляцію?

Якщо одна змінна викликає іншу змінну, чи обов’язково це означає, що ці дві змінні будуть корельовані?

Коротка відповідь: Ні.

Наведені нижче приклади показують чому.

Приклад 1: квадратичне співвідношення

Припустимо, що змінна X змушує змінну Y приймати значення, рівне X ² .

Наприклад:

• Якщо X = -10, то Y = -10 ² = 100
• Якщо X = 0, то Y = 0 ² = 0
• Якщо X = 10, то Y = 10 ² = 100

І так далі.

Якщо ми побудуємо графік залежності між X і Y, це виглядатиме так:

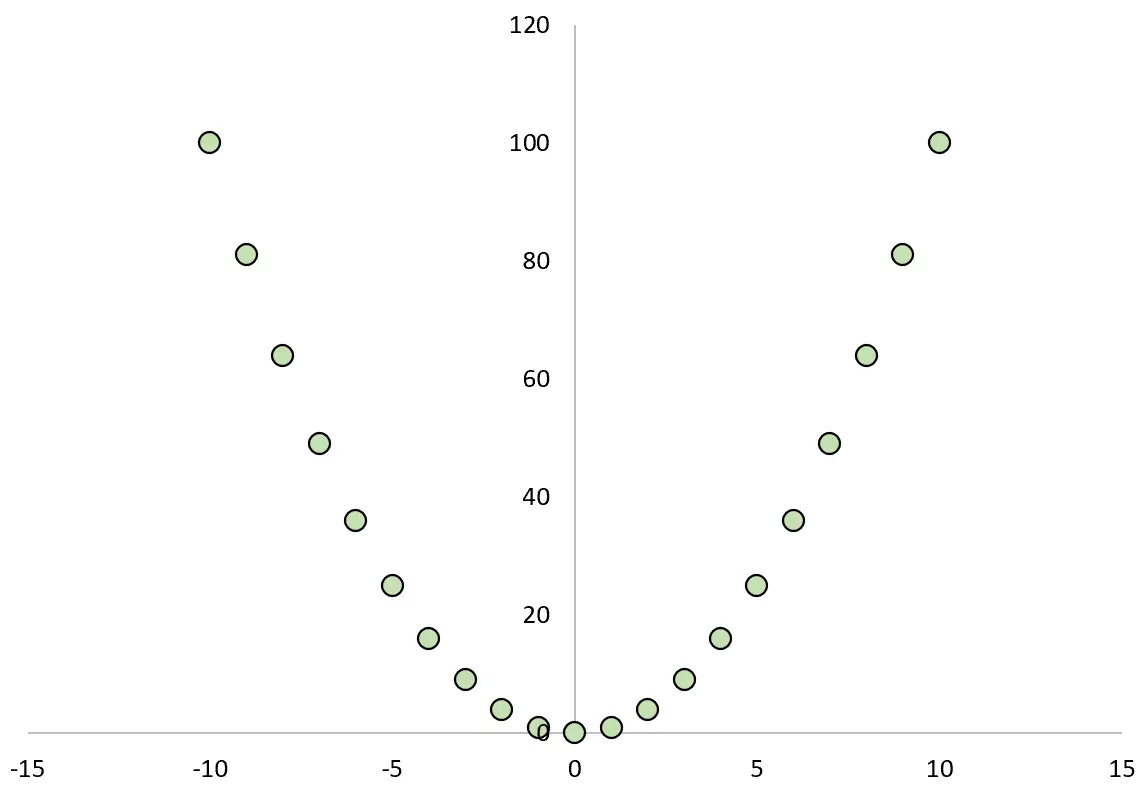
Якщо ми обчислимо коефіцієнт кореляції Пірсона між двома змінними, ми виявимо, що кореляція дорівнює нулю .

Хоча X викликає Y, лінійна кореляція між двома змінними дорівнює нулю.

Приклад 2: квартичне співвідношення

Припустимо, що змінна X змушує змінну Y приймати значення, рівне X ⁴ .

Наприклад:

• Якщо X = -10, то Y = -10 ⁴ = 10 000
• Якщо X = 0, то Y = 0 ⁴ = 0
• Якщо X = 10, то Y = 10 ⁴ = 10 000

І так далі.

Якщо ми побудуємо графік залежності між X і Y, це виглядатиме так:

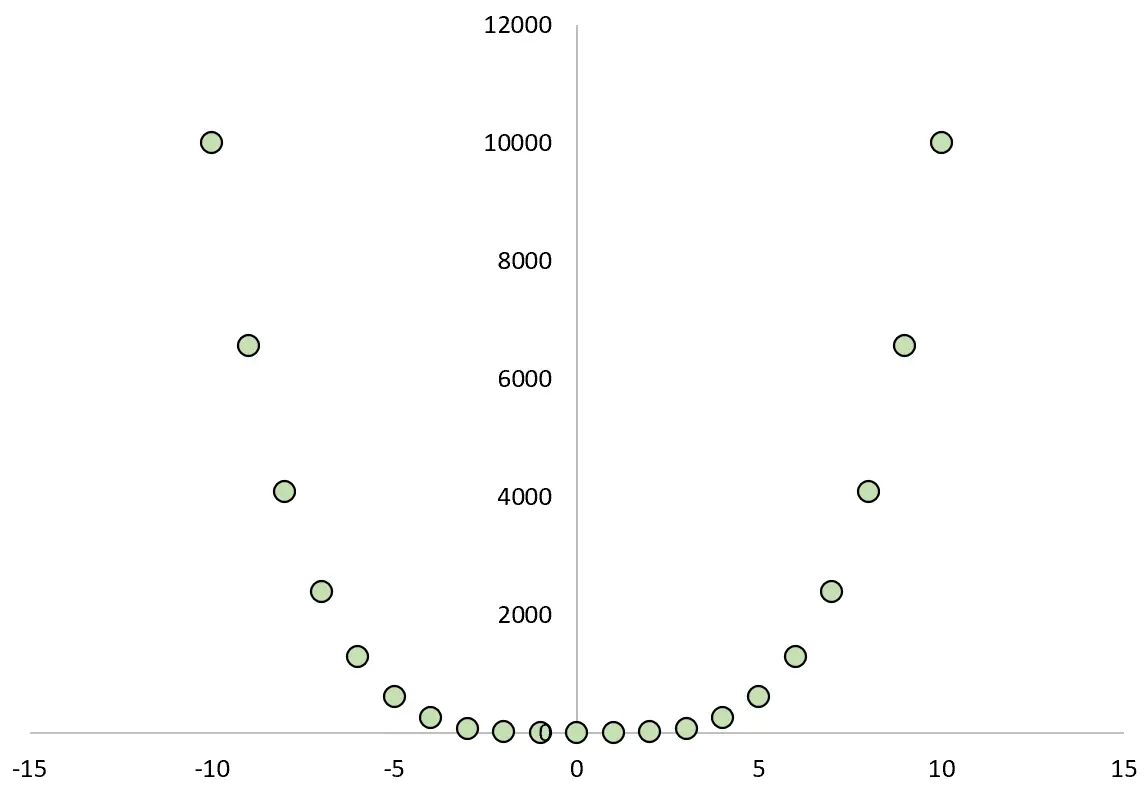
Якщо ми обчислимо коефіцієнт кореляції Пірсона між двома змінними, ми виявимо, що кореляція дорівнює нулю .

Ми знаємо, що X викликає Y, але лінійна кореляція між двома змінними дорівнює нулю.

Приклад 3: косинусне співвідношення

Припустимо, що змінна X змушує змінну Y приймати значення cos(X).

Наприклад:

• Якщо X = -10, то Y = cos(-10) = -0,83907
• Якщо X = 0, то Y = cos(0) = 1
• Якщо X = 10, то Y = cos(10) = -0,83907

І так далі.

Якщо ми побудуємо графік залежності між X і Y, це виглядатиме так:

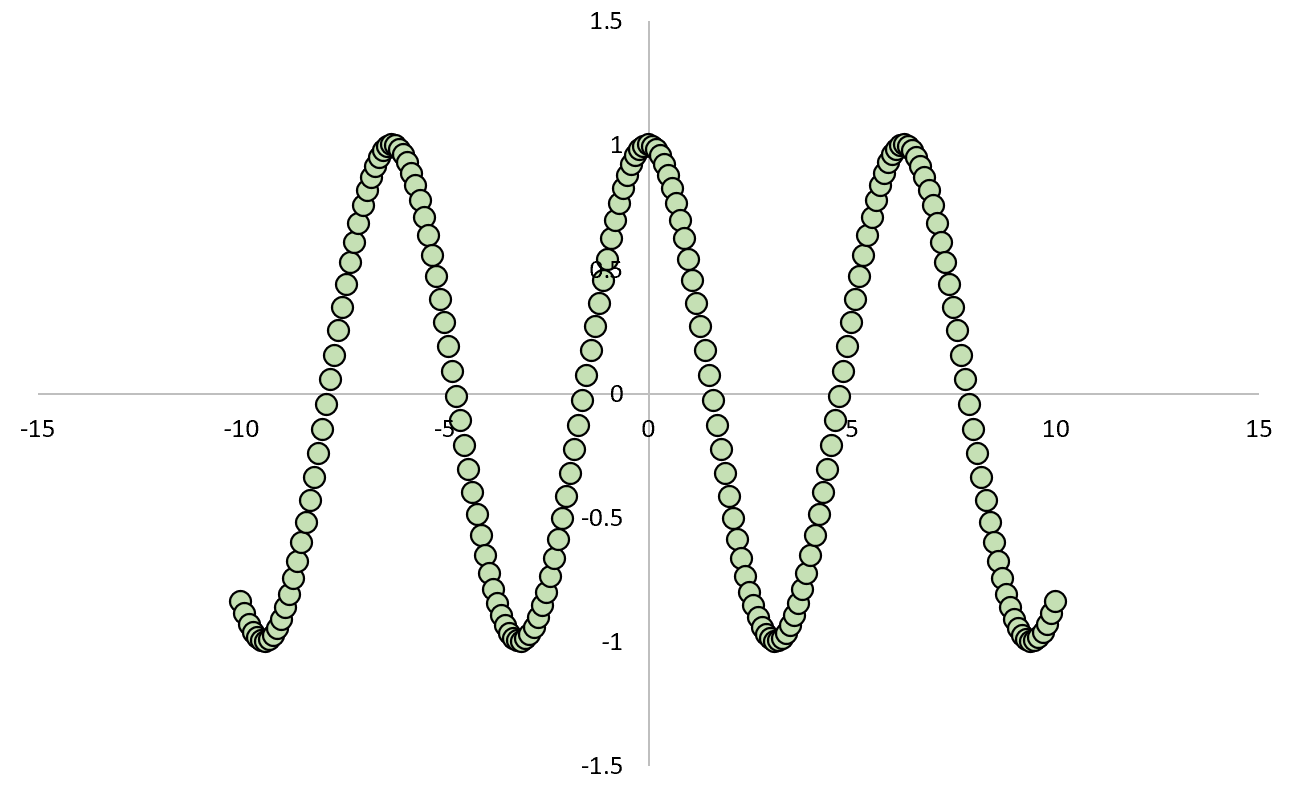
Якщо ми обчислимо коефіцієнт кореляції Пірсона між двома змінними, ми виявимо, що кореляція дорівнює нулю .

Ми знаємо, що X викликає Y, але лінійна кореляція між двома змінними дорівнює нулю.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про кореляцію та причинно-наслідковий зв’язок:

Кореляція не означає причинно-наслідковий зв’язок: 5 конкретних прикладів
Введення в коефіцієнт кореляції Пірсона
Зворотна причинність: визначення та приклади