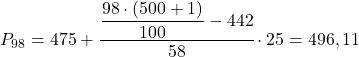Процентилі (статистика)

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке процентиль і як він обчислюється. Ви знайдете розв’язані процентильні вправи та, крім того, зможете обчислити будь-який процентиль вибірки даних за допомогою онлайн-калькулятора.

Що таке процентили?

У статистиці процентилі – це значення, які ділять набір упорядкованих даних на сто рівних частин. Таким чином, процентиль вказує значення, нижче якого опускається відсоток набору даних.

Наприклад, значення 35-го процентиля вище за 35% спостережуваних даних, але нижче за решту даних.

Процентиль позначається великою літерою P та індексом процентиля, тобто 1-й процентиль — P ₁ , 40-й процентиль — P ₄₀ , 79-й процентиль — P ₇₉ і так далі.

👉 Ви можете використовувати калькулятор нижче, щоб обчислити процентилі будь-якого набору даних.

Подібним чином процентили є мірою нецентрального положення разом із квартилями, квінтилями та децилями. Ви можете перевірити значення кожного з цих типів квантилів на нашому веб-сайті.

Слід зазначити, що термін процентиль також використовується для порівняння ваги та зросту дитини зі стандартними значеннями інших немовлят, оскільки існують таблиці зростання із записаними значеннями, які допомагають визначити, чи правильно росте дитина чи ні. . .

Як розрахувати процентиль

Щоб обчислити позицію процентиля ряду статистичних даних, потрібно помножити число процентиля на суму загальної кількості точок даних плюс один і розділити результат на сто.

Таким чином, процентильна формула :

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Будь ласка, зверніть увагу: ця формула повідомляє нам положення процентиля, але не його значення. Процентиль – це дані, розташовані в позиції, отриманій формулою.

Однак іноді результат цієї формули дає нам десяткове число, тому ми повинні розрізняти два випадки залежно від того, чи є результат десятковим числом чи ні:

Якщо результатом формули є число без десяткової частини , процентиль відповідає даним, які знаходяться в позиції, наданій формулою вище.
Якщо результатом формули є число з десятковою частиною , точне значення процентиля обчислюється за такою формулою:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Де x _i і x _i+1 — номери позицій, між якими знаходиться число, отримане за першою формулою, а d — десяткова частина числа, отриманого за першою формулою.

Тепер ви можете подумати, що пошук процентилів статистичної вибірки чи генеральної сукупності є складним, оскільки метод включає багато кроків, але насправді це легко. Прочитайте наступні два конкретних приклади, і я впевнений, що ви зрозумієте це набагато краще.

Примітка . Наукове співтовариство ще не дійшло повної згоди щодо того, як обчислювати процентилі, тому ви можете знайти статистичну книгу, яка пояснює це дещо інакше.

Приклади обчислення процентиля

Як ви бачили вище в поясненні того, як знайти процентиль вибірки, обчислення залежить від того, чи є результат першої формули десятковим чи ні. Ось чому нижче ви знайдете два розв’язаних приклади, по одному для кожного випадку.

Приклад 1

За даними, наведеними в наступній таблиці, обчисліть 1-й, 43-й і 89-й процентилі.

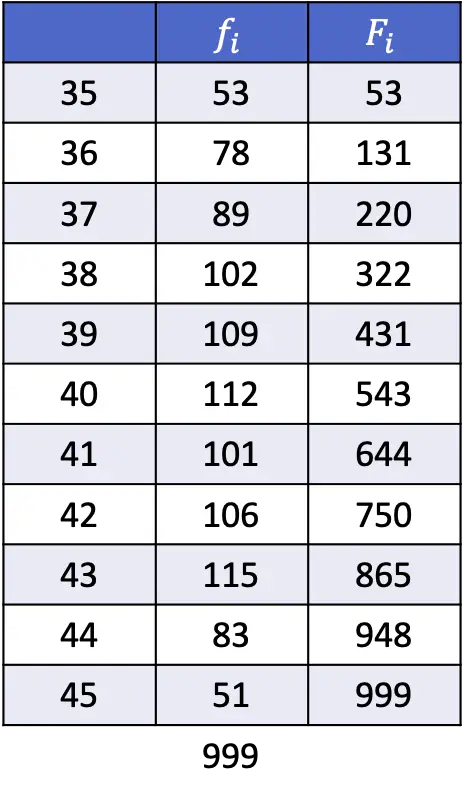
Як пояснювалося в попередньому розділі, формула для знаходження позиції процентиля така:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

У цьому випадку розмір вибірки для цієї вправи становить 999 статистичних даних, тому, щоб обчислити позицію першого процентиля, нам потрібно замінити 999 замість n і 1 замість k :

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

Таким чином, 1-й процентиль буде тим, чия кумулятивна абсолютна частота безпосередньо перевищує 10, що в даному випадку дорівнює 35, оскільки він має кумулятивну абсолютну частоту 53.

Щоб визначити 43-й процентиль, ви повинні використовувати ту саму формулу, але, очевидно, цього разу ми замінимо k на 43.

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

Абсолютна кумулятивна частота безпосередньо над 430 становить 431 з даних 39, тому 43-й процентиль дорівнює 39.

Нарешті, ми застосовуємо ту саму формулу, щоб отримати 89-й процентиль:

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

Сукупна абсолютна частота значення 44 дорівнює 948, що відразу перевищує 890. Отже, 89-й процентиль дорівнює 44.

Приклад 2

Знайдіть 35-й і 67-й процентилі наступного ряду даних:

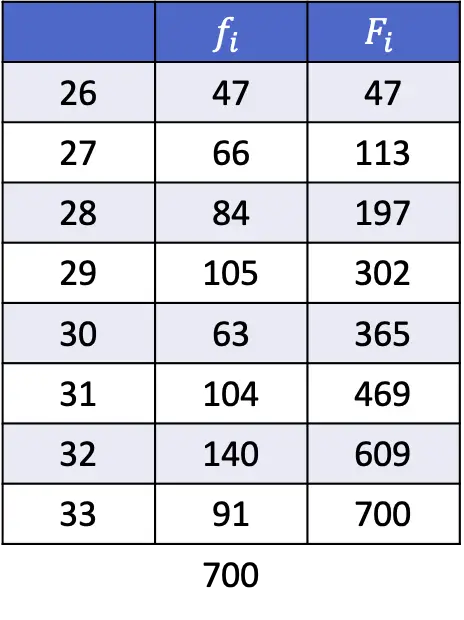
Навіть якщо в цій вправі нам доведеться зробити більше обчислень, принцип залишається тим самим: ми повинні обчислити позицію процентиля за допомогою наступного виразу.

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

Таким чином, щоб обчислити 35-й процентиль, ми замінюємо k на 35, а n на загальну кількість даних, тобто 700:

$\cfrac{35\cdot (700+1)}{100}=245,35$

Але цього разу ми отримали десяткове число з формули, тому нам потрібно застосувати такий алгебраїчний вираз, щоб обчислити точне значення процентиля:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Число, задане першою формулою, дорівнює 245,35, тому 35-й процентиль знаходиться між позиціями 245 і 246, що відповідає значенням 29 і 29 відповідно. Отже, x _i дорівнює 29, x _i+1 дорівнює 29, а d дорівнює десятковій частині отриманого числа, тобто 0,35.

$P_{35}=29+0,35\cdot (29-29)=29$

Щоб знайти 67-й процентиль, нам потрібно використати той самий метод. Спочатку обчислюємо позицію процентиля:

$\cfrac{67\cdot (700+1)}{100}=469,67$

Отримане число 469,67 вказує на те, що процентиль буде знаходитися між позиціями 469 і 470, значення яких дорівнюють 31 і 32. Тому ми використовуємо другу формулу в процесі, щоб знайти точне значення процентиля:

$P_{67}=31+0,67\cdot (32-31)=31,67$

процентний калькулятор

Введіть набір статистичних даних і процентиль, який потрібно обчислити, у наступний калькулятор. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Процентили в згрупованих даних

Щоб обчислити процентиль, коли дані згруповано в групи , спочатку потрібно знайти групу або клас, до якого потрапляє процентиль, використовуючи таку формулу:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Таким чином, процентиль буде в інтервалі, абсолютна частота якого безпосередньо більша за число, отримане в попередньому виразі.

І коли ми вже знаємо інтервал, до якого належить процентиль, ми повинні застосувати таку формулу, щоб знайти точне значення процентиля:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

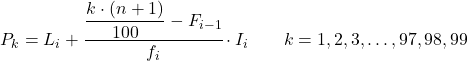
золото:

L _i — нижня межа інтервалу, в якому лежить процентиль.
n – загальна кількість спостережень.
F _i-1 – кумулятивна абсолютна частота попереднього інтервалу.
f _i — абсолютна частота інтервалу, в якому лежить процентиль.
I _i — ширина процентильного інтервалу.

Нижче наведено покрокову вправу щодо отримання процентилів, коли дані виражені в інтервалах. Зокрема, обчислюються 29-й, 52-й і 98-й процентилі.

Дані в цій вибірці згруповано як інтервали, тому нам потрібно виконати два кроки, щоб визначити процентиль: спочатку нам потрібно знайти інтервал, до якого потрапляє процентиль, а потім застосувати формулу для обчислення точного значення процентиля. процентиль.

Таким чином, ми знаходимо положення 29 процентиля за таким виразом:

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

Процентильним інтервалом буде інтервал, сукупна абсолютна частота якого безпосередньо перевищує 145,29, що в даному випадку є інтервалом [350,375), сукупна абсолютна частота якого дорівнює 175. І коли ми знаємо процентиль, ми застосовуємо наступну формулу для його обчислення точне значення:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

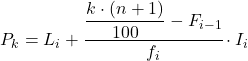
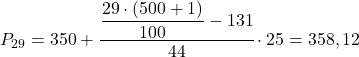
Тепер ми повторюємо ту саму процедуру, щоб обчислити 52-й процентиль. Спочатку обчислимо його інтервал:

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

Інтервал 52-го процентиля дорівнює [400,425), оскільки його кумулятивна абсолютна частота (298) знаходиться безпосередньо над 260,52. Таким чином, точне значення процентиля буде:

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

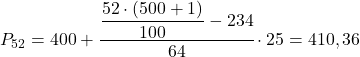
Нарешті ми знайдемо 98 процентиль. Як завжди, ми спочатку обчислюємо інтервал, де він лежить:

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

І як тільки ми знаємо інтервал, де лежить процентиль, ми обчислюємо його точне значення за такою формулою:

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке процентили?

Як розрахувати процентиль

Приклади обчислення процентиля

Приклад 1

Приклад 2

процентний калькулятор

Процентили в згрупованих даних

Про автора

Редакція

Додати коментар