Що таке розподіл вибірки?

Уявіть, що популяція складається з 10 000 дельфінів, і середня вага дельфіна в цій популяції становить 300 фунтів.

Якщо ми візьмемо просту випадкову вибірку з 50 дельфінів із цієї популяції, ми можемо виявити, що середня вага дельфінів у цій вибірці становить 305 фунтів.

Потім, якщо ми візьмемо ще одну просту випадкову вибірку з 50 дельфінів, ми можемо виявити, що середня вага дельфінів у цій вибірці становить 295 фунтів.

Кожного разу, коли ми беремо просту випадкову вибірку з 50 дельфінів, ймовірно, що середня вага дельфінів у вибірці буде близькою до середньої популяції 300 фунтів, але не точно 300 фунтів.

Уявімо, що ми беремо 200 простих випадкових вибірок із 50 дельфінів із цієї популяції та створюємо гістограму середньої ваги кожної вибірки:

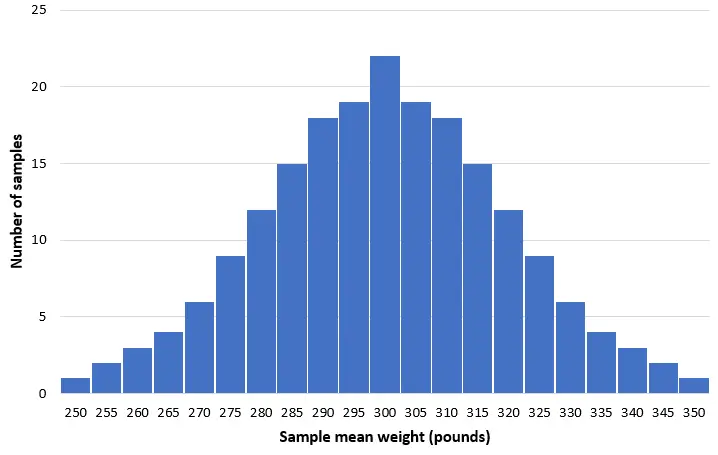
У більшості зразків середня вага буде близько 300 фунтів. У рідкісних випадках ми можемо взяти зразок із маленькими дельфінами, середня вага яких становить лише 250 фунтів. Або ми можемо взяти повну пробу афалін, середня вага яких становить 350 фунтів. Загалом розподіл вибіркових середніх буде приблизно нормальним із центром розподілу в істинному центрі сукупності.

Цей розподіл вибіркових середніх відомий як вибірковий розподіл середнього і має такі властивості:

_µx = µ

де μ _x – вибіркове середнє значення, а μ – середнє значення сукупності.

_σx = σ/√n

де σ _x — стандартне відхилення вибірки, σ — стандартне відхилення сукупності, а n — розмір вибірки.

Наприклад, у цій популяції дельфінів ми знаємо, що середня вага становить μ = 300. Таким чином, середнє значення вибіркового розподілу дорівнює μ _x = 300 .

Припустимо, ми також знаємо, що стандартне відхилення популяції становить 18 фунтів. Таким чином, стандартне відхилення вибірки становить σ _x = 18/ √50 = 2,546 .

Вибірковий розподіл частки

Розглянемо ту саму популяцію з 10 000 дельфінів. Припустимо, що 10% дельфінів чорні, а решта сірі. Припустимо, ми беремо просту випадкову вибірку з 50 дельфінів і знаходимо, що 14% дельфінів у цій вибірці чорні. Далі ми беремо ще одну просту випадкову вибірку з 50 дельфінів і знаходимо, що 8% дельфінів у цій вибірці чорні.

Уявіть, що ми беремо 200 простих випадкових вибірок із 50 дельфінів із цієї популяції та створюємо гістограму частки чорних дельфінів у кожній вибірці:

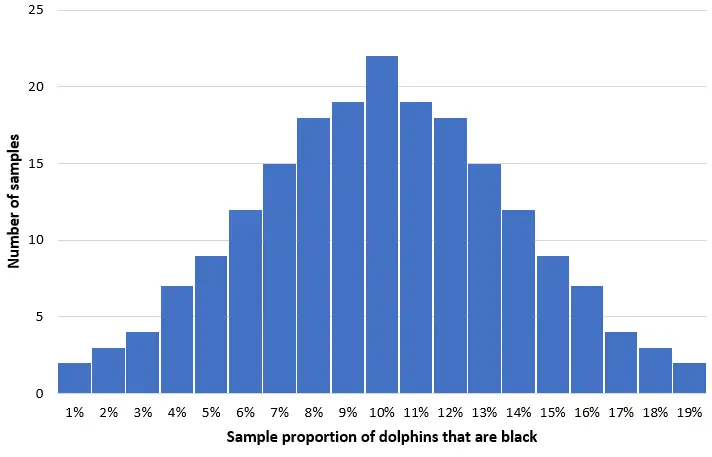
У більшості зразків частка чорних дельфінів буде близькою до фактичної популяції в 10%. Розподіл вибіркової частки чорних дельфінів буде приблизно нормальним, з центром розподілу, розташованим у справжньому центрі популяції.

Цей розподіл пропорцій вибірки відомий як розподіл пропорцій вибірки та має такі властивості:

_µp = P

де p — частка вибірки, а P — частка сукупності.

σ _p = √ (P)(1-P) / n

де P — частка сукупності, а n — розмір вибірки.

Наприклад, у цій популяції дельфінів ми знаємо, що справжня частка чорних дельфінів становить 10% = 0,1. Таким чином, середнє значення пропорційного розподілу вибірки становить μ _p = 0,1 .

Припустимо, ми також знаємо, що стандартне відхилення популяції становить 18 фунтів. Таким чином, стандартне відхилення вибірки становить σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 .

Встановити нормальний стан

Щоб використовувати наведені вище формули, розподіл вибірки має бути нормальним.

Згідно з центральною граничною теоремою , вибірковий розподіл вибіркового середнього є приблизно нормальним, якщо розмір вибірки достатньо великий, навіть якщо розподіл генеральної сукупності не є нормальним . У більшості випадків ми вважаємо розмір вибірки 30 або більше достатньо великим.

Вибірковий розподіл частки вибірки є приблизно нормальним, якщо очікувана кількість успіхів і невдач становить принаймні 10.

Приклади

Ми можемо використовувати вибіркові розподіли для обчислення ймовірностей.

Приклад 1: Певна машина створює файли cookie. Розподіл ваги цього печива зміщений вправо із середнім значенням 10 унцій і стандартним відхиленням 2 унції. Якщо ми візьмемо просту випадкову вибірку зі 100 печива, виготовлених цією машиною, яка ймовірність того, що середня вага печива в цій вибірці буде менше 9,8 унцій?

Крок 1: Встановлення нормального стану.

Нам потрібно переконатися, що розподіл вибіркових середніх є нормальним. Оскільки розмір нашої вибірки більший або дорівнює 30, відповідно до центральної граничної теореми, ми можемо припустити, що розподіл вибіркових середніх є нормальним.

Крок 2: Знайдіть середнє значення та стандартне відхилення розподілу вибірки.

_µx = µ

_σx = σ/√n

μ _x = 10 унцій

σ _x = 2/ √100 = 2/10 = 0,2 унції

Крок 3. Використовуйте калькулятор площі Z-показника , щоб визначити ймовірність того, що середня вага печива в цьому зразку становить менше 9,8 унцій.

Введіть наступні цифри в калькулятор зони оцінки Z. Ви можете залишити поле «Необроблений результат 2» порожнім, оскільки в цьому прикладі ми знаходимо лише одне число.

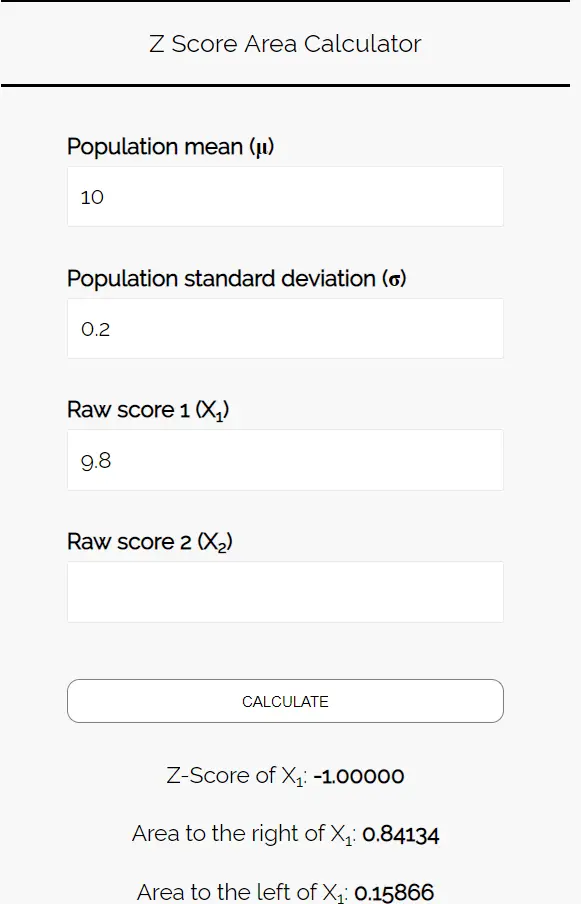
Оскільки ми хочемо знати ймовірність того, що середня вага печива в цьому зразку менше 9,8 унцій, нас цікавить область ліворуч від 9,8. Калькулятор говорить нам, що ця ймовірність становить 0,15866 .

Приклад 2: Згідно з загальношкільним дослідженням, 87% учнів певної школи віддають перевагу піці, ніж морозиву. Припустимо, ми беремо просту випадкову вибірку з 200 студентів. Яка ймовірність того, що частка студентів, які віддають перевагу піці, становить менше 85%?

Крок 1: Встановлення нормального стану.

Пам’ятайте, що вибірковий розподіл вибіркової частки є приблизно нормальним, якщо очікувана кількість «успішних» і «невдалих» становить принаймні 10.

У цьому випадку очікувана кількість студентів, які віддадуть перевагу піці, становить 87% * 200 студентів = 174 студенти. Очікувана кількість студентів, які не віддадуть перевагу піці, становить 13% * 200 студентів = 26 студентів. Оскільки обидва ці числа не менше 10, можна припустити, що вибірковий розподіл частки студентів, які віддадуть перевагу піці, є приблизно нормальним.

Крок 2: Знайдіть середнє значення та стандартне відхилення розподілу вибірки.

_µp = P

σ _p = √ (P)(1-P) / n

_µp = 0,87

σ _p = √ (0,87)(1-0,87) / 200 = 0,024

Крок 3. Використовуйте калькулятор площі Z-Score , щоб визначити ймовірність того, що частка студентів, які віддають перевагу піці, становить менше 85%.

Введіть наступні цифри в калькулятор зони оцінки Z. Ви можете залишити поле «Необроблений результат 2» порожнім, оскільки в цьому прикладі ми знаходимо лише одне число.

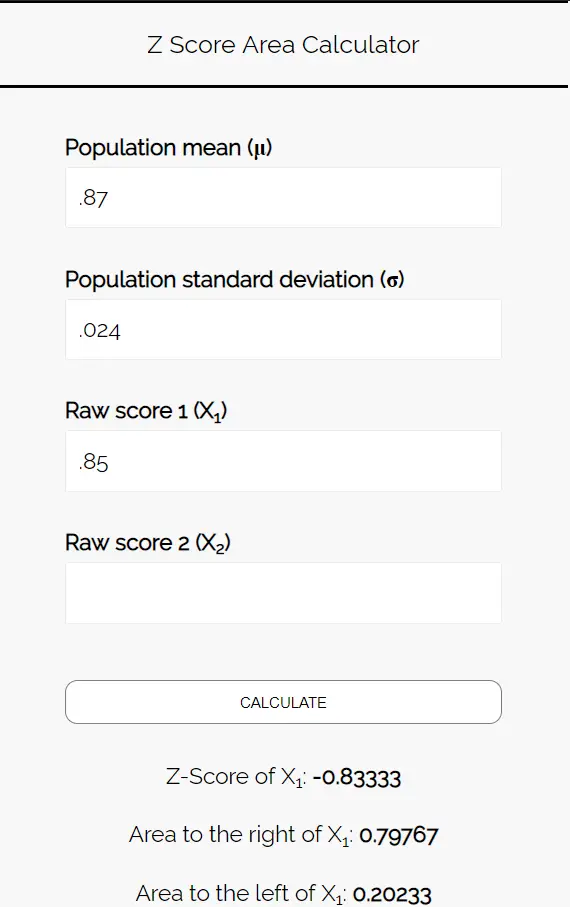
Оскільки ми хочемо знати ймовірність того, що частка студентів, які віддають перевагу піці, становить менше 85%, нас цікавить область ліворуч від 0,85. Калькулятор говорить нам, що ця ймовірність становить 0,20233 .