Введення в розподіл пуассона

Розподіл Пуассона є одним із найпопулярніших розподілів у статистиці.

Щоб зрозуміти розподіл Пуассона, корисно спочатку зрозуміти експерименти Пуассона.

Експерименти з рибками

Дослід Пуассона — це експеримент, який має такі властивості:

• Кількість успіхів експерименту можна порахувати.
• Відомо середнє число успіхів, які відбулися протягом певного часового (або просторового) інтервалу.
• Кожен результат незалежний.
• Імовірність успіху пропорційна розміру інтервалу.

Прикладом експерименту Пуассона є кількість пологів за годину в даній лікарні. Наприклад, припустімо, що в конкретній лікарні в середньому відбувається 10 пологів на годину. Це експеримент Пуассона, оскільки він має такі чотири властивості:

• Число успіхів експерименту можна порахувати – Ми можемо порахувати кількість народжень.
• Середня кількість пологів, які відбуваються протягом певного інтервалу часу, відома – відомо, що в середньому відбувається 10 пологів на годину.
• Кожен результат є незалежним – Імовірність того, що одна мати народить у певну годину, не залежить від ймовірності того, що інша мати народить.
• Імовірність успіху пропорційна розміру інтервалу: чим довший часовий інтервал, тим вища ймовірність народження.

Ми можемо використовувати розподіл Пуассона, щоб відповісти на питання про ймовірності цього експерименту Пуассона, наприклад:

• Яка ймовірність того, що протягом години відбудеться більше 12 пологів?
• Яка ймовірність того, що за певну годину відбудеться менше 5 пологів?
• Яка ймовірність того, що за певну годину відбудеться від 8 до 11 пологів?

Розподіл риби

Розподіл Пуассона описує ймовірність отримання k успіхів протягом заданого інтервалу часу.

Якщо випадкова величина X відповідає розподілу Пуассона, то ймовірність успіху X = k можна знайти за такою формулою:

P(X=k) = λ ^k * e ^{– λ} / k!

золото:

• λ: середня кількість успіхів протягом певного інтервалу
• k: кількість успіхів
• e: константа, що дорівнює приблизно 2,71828

Наприклад, припустимо, що в одній лікарні в середньому відбувається 2 пологи на годину. Ми можемо використовувати наведену вище формулу, щоб визначити ймовірність пережити 0, 1, 2, 3 народження тощо. в певну годину:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707

P(X=3) = 2 ³ * e ^{– 2/3} ! = 0,1805

Ми можемо розрахувати ймовірність будь-якої кількості народжень до нескінченності. Потім ми створюємо просту гістограму, щоб візуалізувати цей розподіл ймовірностей:

Обчислення кумулятивних ймовірностей Пуассона

За допомогою наведеної вище формули легко обчислити одну ймовірність Пуассона (наприклад, ймовірність того, що в лікарні буде 3 пологів за певну годину), але для обчислення сукупної ймовірності Пуассона нам потрібно додати окремі ймовірності.

Наприклад, скажімо, ми хочемо знати ймовірність того, що в лікарні буде 1 або менше пологів за певну годину. Щоб обчислити цю ймовірність, ми використаємо таку формулу:

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

Це називається кумулятивною ймовірністю , оскільки вона передбачає додавання кількох ймовірностей. Ми можемо обчислити кумулятивну ймовірність народження k або менше за певну годину за подібною формулою:

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Ми можемо обчислити ці кумулятивні ймовірності для будь-якої кількості народжень до нескінченності. Потім ми можемо створити гістограму для візуалізації цього кумулятивного розподілу ймовірностей:

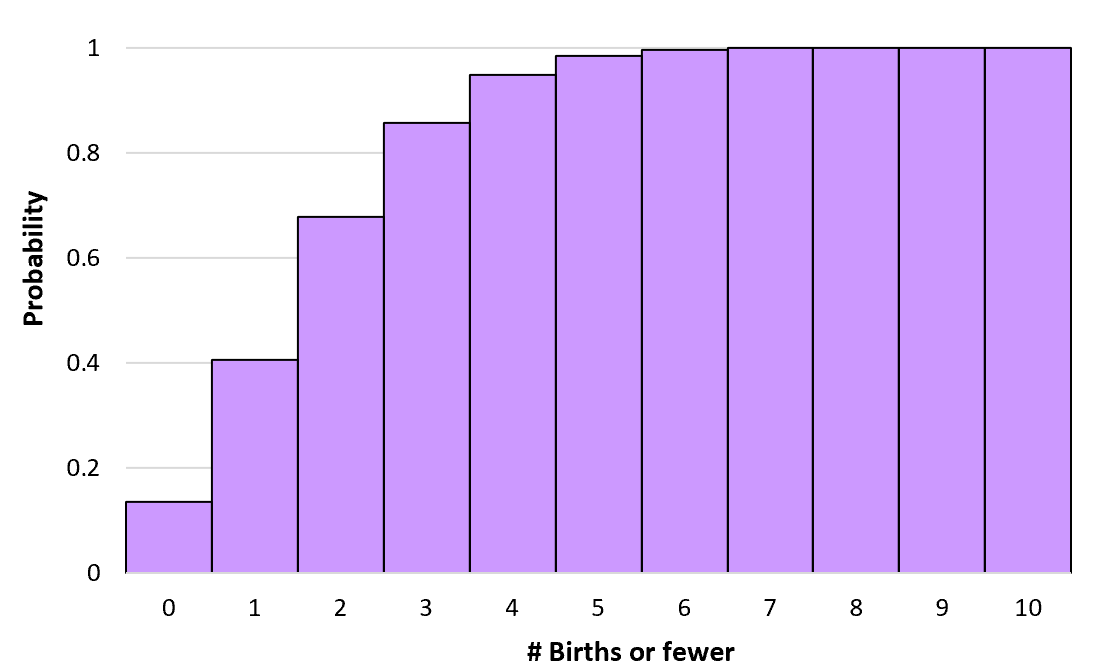
Властивості розподілу Пуассона

Розподіл Пуассона має такі властивості:

Середнє значення розподілу дорівнює λ .

Дисперсія розподілу також дорівнює λ .

Стандартне відхилення розподілу дорівнює √ λ .

Наприклад, припустимо, що в лікарні в середньому відбувається 2 пологи на годину.

Середня кількість пологів, очікуваних за певну годину, становить λ = 2 пологи.

Дисперсія кількості народжень, яку ми очікуємо, становить λ = 2 народження.

Проблеми практики розподілу риби

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про розподіл Пуассона.

Примітка: ми будемо використовувати калькулятор розподілу Пуассона , щоб обчислити відповіді на ці запитання.

Проблема 1

Питання: Ми знаємо, що певний сайт здійснює 10 продажів на годину. Яка ймовірність того, що сайт зробить рівно 8 продажів за певну годину?

Відповідь: використовуючи калькулятор розподілу Пуассона з λ = 10 і x = 8, ми знаходимо, що P(X=8) = 0,1126 .

Проблема 2

Питання: Ми знаємо, що певний агент з нерухомості здійснює в середньому 5 продажів на місяць. Яка ймовірність того, що вона здійснить більше ніж 7 продажів за певний місяць?

Відповідь: Використовуючи калькулятор розподілу Пуассона з λ = 5 і x = 7, ми знаходимо, що P(X>7) = 0,13337 .

Проблема 3

Питання: Ми знаємо, що в певній лікарні відбувається 4 пологи на годину. Яка ймовірність того, що за певну годину буде 4 або менше пологів?

Відповідь: Використовуючи калькулятор розподілу Пуассона з λ = 4 і x = 4, ми знаходимо, що P(X≤4) = 0,62884 .

Додаткові ресурси

У наступних статтях пояснюється, як використовувати розподіл Пуассона в різних статистичних програмах:

Як використовувати розподіл Пуассона в R
Як використовувати розподіл Пуассона в Excel
Як обчислити ймовірності Пуассона на калькуляторі TI-84
Реальні приклади розподілу Пуассона
Калькулятор розподілу риби