Середня різниця

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке середнє відхилення та як воно обчислюється. Ви також знайдете конкретні приклади обчислення середнього відхилення. І, крім того, ви зможете розрахувати середнє відхилення будь-якого набору статистичних даних за допомогою онлайн-калькулятора.

Що таке середнє відхилення?

Середнє відхилення , яке також називають середнім абсолютним відхиленням , є мірою статистичної дисперсії.

Середнє відхилення набору даних є середнім абсолютних відхилень . Отже, середнє відхилення дорівнює сумі відхилень кожного елемента даних від середнього арифметичного, поділеній на загальну кількість елементів даних.

Іншими словами, формула середнього відхилення має такий вигляд:

👉 Ви можете скористатися калькулятором нижче, щоб обчислити середнє відхилення будь-якого набору даних.

У статистиці середнє відхилення також називають середнім абсолютним відхиленням .

Інтерпретація середнього відхилення здійснюється таким чином: чим більше значення середнього відхилення, це означає, що дані в середньому далі від середнього арифметичного; і навпаки, чим менше середнє відхилення, тим ближче значення. дані є. Тому середнє відхилення вказує на дисперсію ряду даних.

Іншими мірами, які вважаються розподіленими, є діапазон, інтерквартильний діапазон, стандартне відхилення (або стандартне відхилення), дисперсія та коефіцієнт варіації.

Як розрахувати середнє відхилення

Щоб обчислити середнє відхилення ряду даних, потрібно виконати наступні кроки:

Обчислити середнє арифметичне набору статистичних даних.
Обчисліть відхилення кожної точки даних від середнього, визначене як абсолютне значення різниці між даними та середнім.
Складіть усі різниці, обчислені на попередньому кроці.
Розділіть на загальну кількість даних. Отриманий результат є середнім відхиленням ряду даних.

Підсумовуючи, формула, яку необхідно застосувати для визначення середнього відхилення, така:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Приклад розрахунку середнього відхилення

Розглядаючи визначення середнього відхилення, нижче наведено покроковий приклад обчислення середнього відхилення статистичної вибірки. Таким чином ви краще зрозумієте, як отримати середнє відхилення.

Аналітик вивчає економічні результати компанії за минулий рік і має інформацію про прибуток, отриманий компанією за кожен квартал цього року: 2, 3, 7 і 5 мільйонів доларів. Яке середнє відхилення даних?

Спочатку нам потрібно усереднити дані, тому ми підсумовуємо та ділимо на загальну кількість спостережень (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

Після того, як ми обчислили середнє арифметичне, ми використовуємо формулу середнього відхилення:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Підставляємо дані у формулу:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

Робимо обчислення в чисельнику:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

І, нарешті, ми ділимо на загальну кількість даних, щоб отримати середнє відхилення вибірки:

$D_{\overline{x}}=1,75$

Калькулятор середнього відхилення

Введіть набір статистичних даних у наступний калькулятор, щоб обчислити його середнє відхилення. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Середнє відхилення для згрупованих даних

Щоб обчислити середнє відхилення даних, згрупованих в інтервали, необхідно виконати наступні кроки:

Визначити середнє арифметичне сукупності статистичних даних. Оскільки дані згруповані, вираз для обчислення середнього має вигляд:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Обчисліть відхилення кожного інтервалу від середнього, яке еквівалентно абсолютному значенню різниці між класною оцінкою та середнім.

$|x_i-\overline{x}|$

Помножте відхилення кожного інтервалу на його абсолютну частоту.

$|x_i-\overline{x}|\cdot f_i$

Складіть усі результати з попереднього кроку, а потім розділіть на загальну кількість даних. Отриманий результат є середнім відхиленням вибірки, згрупованої в інтервали.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

На закінчення формула для отримання середнього відхилення від згрупованих даних має вигляд:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Коли дані групуються, це зазвичай означає, що даних багато, і пошук середнього відхилення включає багато кроків. Тому для виконання розрахунку зазвичай використовують частотні таблиці.

Нижче наведено покрокову вправу, як обчислити середнє відхилення, коли дані згруповано в інтервали:

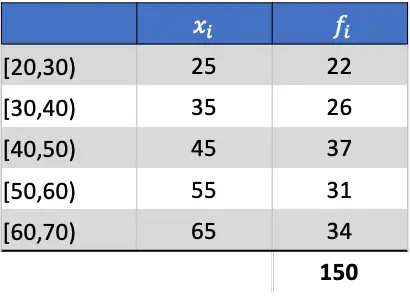
Перше, що потрібно зробити, це обчислити середнє значення згрупованих даних. Для цього ми додаємо стовпець до таблиці, помноживши примітку класу на її частоту:

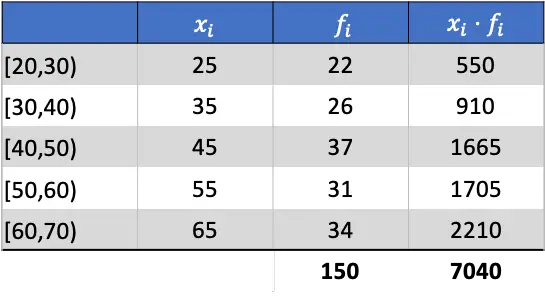
Отже, середнє арифметичне буде результатом ділення суми доданого стовпця на суму абсолютних частот:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Тепер, коли ми знаємо середнє значення даних, ми можемо додати всі необхідні стовпці, щоб знайти середнє відхилення:

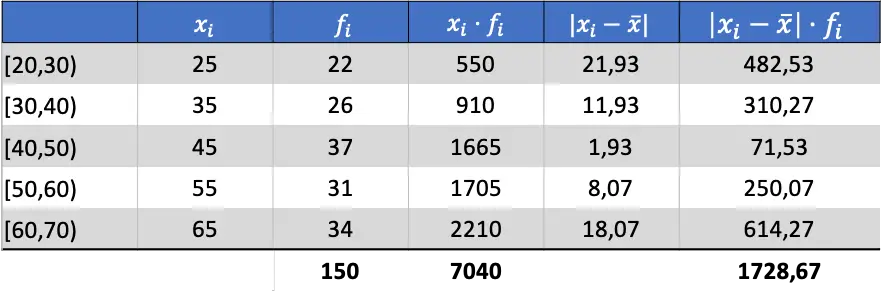
Таким чином, щоб отримати середнє відхилення, необхідно суму останнього стовпця розділити на загальну кількість спостережень:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше