Гармонійний середній

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

Тут ми пояснюємо, що таке середнє гармонічне і як воно обчислюється (формула). Крім того, крок за кроком обчислюється середнє гармонічне прикладу. Ви також знайдете калькулятор для визначення середнього гармонічного будь-якого набору даних. І, нарешті, ви зможете побачити властивості середнього гармонічного.

Що таке середнє гармонічне?

Середнє гармонічне — це міра центрального положення описової статистики. Середнє гармонійне обчислюється шляхом ділення загальної кількості статистичних даних на суму зворотних величин кожного значення.

Гармонічне середнє використовується для обчислення середніх швидкостей, часу або проведення електронних розрахунків. Ця особливість відрізняє гармонічне середнє від інших типів середніх, які часто використовуються для розрахунку середніх цін або відсотків.

Отже, формула для середнього гармонічного має такий вигляд:

Гармонічне середнє зазвичай позначається великою H.

Інші типи середнього, які існують, це середнє арифметичне, середнє зважене, середнє квадратичне та середнє геометричне. Гармонічне середнє має переваги та недоліки порівняно з іншими типами середнього, нижче ми побачимо, що це таке.

Як обчислити середнє гармонічне

Щоб обчислити середнє гармонічне, необхідно виконати наступні кроки:

Обчисліть зворотну величину кожного статистичного даного у вибірці.
Додайте всі обчислені зворотні значення.
Розділіть загальну кількість даних на суму, знайдену на попередньому кроці.
Отриманий результат є середнім гармонійним статистичної вибірки.

👉 Як бачите, визначення середнього гармонійного набору даних вимагає багатьох операцій, тому робити це вручну досить трудомістко. Тому для розрахунку середнього гармонічного ми рекомендуємо скористатися калькулятором, наведеним нижче.

Приклад середнього гармонічного

Ознайомившись із теорією середнього гармонічного, ми побачимо, як знайти середнє гармонічне набору даних, розв’язуючи покроковий приклад ціни акції.

Людина купує акції компанії щороку протягом 5 років поспіль. Протягом цього періоду ціна акцій сильно коливалася: у перший рік кожна акція коштувала 7 євро, у другий рік 10 євро, у третій рік 15 євро, у четвертий рік компанія зазнала значних фінансових збитків і ціна впала до 6 євро за акцію, і зрештою, на п’ятому році компанія зробила великі інвестиції, які підняли ціну до 11 євро. Якою була середня ціна покупки акцій?

Одним із варіантів буде обчислення середнього арифметичного, тобто складання всіх цін і розділення їх на п’ять. Однак, оскільки закупівлі здійснювалися в різні роки, взяти середнє арифметичне було б помилкою. Тому ми повинні знайти середнє гармонічне всіх цін.

Далі ми застосовуємо формулу середнього гармонічного:

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+\frac{1}{x_4}+\frac{1}{x_5}}$

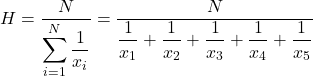
А потім підставляємо проблемні цінові значення в формулу і обчислюємо середнє гармонічне:

$\displaystyle H=\frac{5}{\displaystyle\frac{1}{7}+\frac{1}{10}+\frac{1}{15}+\frac{1}{6}+\frac{1}{11}}=8,82$

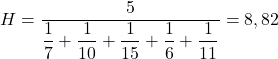
Ви повинні поставити п’ять у чисельник дробу, тому що є п’ять різних частин інформації.

Таким чином, середня ціна акцій, які ви придбали протягом цього періоду, становить 8,82 євро за акцію.

Калькулятор середнього гармонічного

За допомогою наступного калькулятора ви можете обчислити середнє гармонічне будь-якого набору статистичних даних.

Ви повинні вводити числа, використовуючи крапку як десятковий роздільник і розділяючи числа пробілом. Пам’ятайте, що для визначення середнього гармонічного жодне значення не може дорівнювати нулю.

Властивості середнього гармонічного

Середнє гармонічне має такі характеристики:

Великі значення мало впливають на середнє гармонічне ансамблю, тобто дуже велике значення відносно інших даних не викличе помітної зміни середнього гармонічного.

З іншого боку, мале значення сильно впливає на середнє гармонійне значення ансамблю, значно знижуючи його значення. Дійсно, величини, зворотні знаменнику формули, тоді приймають дуже великі значення.

Гармонічне середнє не можна обчислити, якщо будь-які дані дорівнюють нулю, оскільки це призведе до невизначеності у формулі. У такому випадку середнє гармонічне вважається невизначеним.

Величина, зворотна середньому гармонічному, еквівалентна середньому арифметичному зворотних величин спостережень.

Для тієї самої групи даних середнє гармонічне буде менше або дорівнює середньому арифметичному.

$\cfrac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}\leq \cfrac{x_1+x_2+\dots+x_N}{N}$

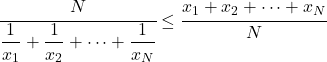
Обчисліть середнє гармонічне за допомогою Excel

Як ми бачили, обчислення середнього гармонічного вручну може бути досить виснажливим, оскільки потрібно виконати багато обчислень. І це стає ще складнішим, коли у вас є великий обсяг даних. Тому для знаходження середнього гармонічного рекомендуємо скористатися калькулятором або програмою Excel.

Середнє гармонічне в Excel обчислюється за формулою MEAN.ARMO . Тобто, щоб обчислити середнє гармонічне набору даних, потрібно скопіювати їх на аркуш Excel і ввести всі дані у функцію MEAN.ARMO .

Наприклад, щоб отримати середнє гармонічне вправи, яку ми розв’язали вище, ви пишете в клітинці Excel =MEDIA.ARMO(7;10;15;6;11) .

Ви повинні мати на увазі, що якщо будь-яке зі значень дорівнює нулю, функція поверне помилку, оскільки середнє гармонійне набору статистичних значень неможливо визначити, якщо будь-яке з них дорівнює нулю.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше