Геометричні засоби

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

У цій статті ми пояснюємо, що таке середнє геометричне, як воно обчислюється та яка різниця між середнім геометричним і середнім арифметичним. Ви також зможете побачити крок за кроком розв’язану вправу із середнім геометричним і які властивості цього типу середнього. Нарешті, ви знайдете калькулятор для обчислення середнього геометричного будь-якого набору даних.

Що таке середнє геометричне?

Середнє геометричне є мірою центральності описової статистики. Середнє геометричне набору статистичних даних дорівнює кореню n-ої частини з добутку всіх значень.

Середнє геометричне використовується в бізнес-фінансах для розрахунку норм прибутку, середніх відсотків і складних відсотків.

Отже, формула для середнього геометричного має такий вигляд:

Середнє геометричне можна розрахувати лише тоді, коли всі дані у вибірці позитивні. Тому що, якщо значення від’ємне, корінь матиме від’ємний розв’язок або не матиме розв’язку, з іншого боку, якщо дані дорівнюють нулю, тоді множення даних дасть нуль і, отже, середнє геометричне дорівнюватиме 0.

Середнє геометричне — не єдиний тип середнього, який існує, існує також середнє арифметичне, середнє зважене, середнє квадратичне та середнє гармонічне.

Різниця між середнім геометричним і середнім арифметичним

Основна відмінність між середнім геометричним і середнім арифметичним полягає в тому, що середнє геометричне менш чутливе до екстремальних значень, ніж середнє арифметичне. Крім того, середнє арифметичне можна обчислити з від’ємними та нульовими значеннями, тоді як середнє геометричне можна обчислити лише з додатними значеннями.

Подібним чином середнє геометричне буде, як правило, нижчим за середнє арифметичне для того самого набору даних.

Слід також зазначити, що розрахунок середнього геометричного більш складний і тому його статистичну значущість складніше інтерпретувати.

Коротше кажучи, середнє геометричне має переваги та недоліки порівняно із середнім арифметичним і, залежно від характеру даних, доцільно буде розрахувати те чи інше середнє.

Як обчислити середнє геометричне

Щоб обчислити середнє геометричне, необхідно виконати наступні дії:

Обчислити добуток усіх статистичних даних у вибірці.
Знайдіть корінь n-ної частини з обчисленого добутку.
Отриманий результат є середнім геометричним статистичної вибірки.

Як бачите, знайти середнє геометричне набору даних відносно просто за допомогою калькулятора або комп’ютерної програми, оскільки вам потрібно лише обчислити добуток і корінь. Навпаки, розрахунок вручну робити досить копітко.

👉 Ось чому ми рекомендуємо використовувати калькулятор нижче для обчислення середнього геометричного набору даних.

Приклад середнього геометричного

Коли ми ознайомимося з теорією про середнє геометричне, ми наведемо приклад, щоб ви могли точно побачити, як отримати середнє геометричне.

Відомі економічні результати компанії за останні п’ять років. У перший рік компанія отримала економічну рентабельність 10%, у другий рік прибуток досяг 23%, у третій рік зароблені гроші становили 16%, у четвертий рік вона досягла економічної рентабельності 7%, а інвестиції на п’ятий рік представляв прибуток 20%. Вас просять обчислити середнє значення всіх відсотків.

Як ми бачили, щоб обчислити середнє відсоткових значень, слід використовувати не середнє арифметичне, а краще виконати обчислення із середнім геометричним.

Тому застосовуємо формулу середнього геометричного:

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

І підставляємо в формулу значення прикладу і проводимо розрахунок:

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Зверніть увагу, що у нас є п’ять точок даних, тому ми обчислюємо п’ятий корінь.

Числовий результат середнього геометричного дорівнює 1,15, що означає, що економічне зростання компанії становило в середньому 15% щороку.

Майте на увазі, що ми змогли отримати середнє геометричне, оскільки всі значення були додатними, але якби будь-який відсоток був від’ємним, нам довелося б помістити дані у формулу як додатний десятковий дроб із цілою частиною. дорівнює нулю. Наприклад, зростання на -30% має бути виражено у формулі як 0,70 (1-0,3=0,7).

Калькулятор середнього геометричного

Підключіть будь-який зразок статистики до калькулятора нижче, щоб знайти його середнє геометричне. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником. Пам’ятайте, що ви не можете визначити середнє геометричне, якщо значення від’ємне або дорівнює нулю.

Властивості середнього геометричного

Середнє геометричне має такі характеристики:

Це тип середнього значення, який дуже корисний для знаходження середнього значення відсотків або індексів.

Його можна розрахувати, лише якщо всі дані позитивні.

Геометричним значенням середнього геометричного двох чисел a і b є сторона квадрата, площа якого дорівнює площі прямокутника, сторони якого дорівнюють a і b .

$MG(a,b)=\sqrt{a\cdot b}$

Геометричним змістом середнього геометричного трьох чисел a , b і c є сторона куба, об’єм якого еквівалентний паралелепіпеду зі сторонами a , b і c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Логарифм середнього геометричного набору даних дає середнє арифметичне логарифмів того самого набору.

Середнє геометричне набору значень завжди буде менше або дорівнює середньому арифметичному.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

Середнє геометричне зважене обчислюється так само, як середнє геометричне, але шляхом додавання ваг до експоненти кожного елемента даних для зважування статистичних значень.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

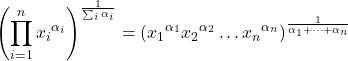
Обчислити середнє геометричне в Excel

Нарешті, давайте подивимося, як знайти середнє геометричне набору даних за допомогою програми Excel.

Щоб обчислити середнє геометричне в Excel, потрібно скористатися функцією СРЕДСТВА.ГЕОМ. Просто введіть усі значення, з яких ви хочете взяти середнє геометричне, і функція поверне результат середнього геометричного.

Наприклад, щоб визначити середнє геометричне для наведеного вище прикладу, ви повинні написати у полі Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Ви повинні мати на увазі, що якщо будь-яке зі значень дорівнює нулю або негативне, функція поверне помилку.

Як бачите, обчислити середнє геометричне в Excel набагато простіше і швидше, оскільки потрібно просто скопіювати дані на аркуш і скористатися формулою.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше