Середнє зважене

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

Тут ми пояснюємо, що таке середньозважене значення та як воно обчислюється. Ви зможете побачити розв’язану вправу про те, як ми знаходимо зважене середнє. Більше того, ви можете обчислити середньозважене значення будь-якого набору даних за допомогою калькулятора в кінці.

Що таке середньозважений показник?

Середньозважене значення є мірою центральності описової статистики. Щоб обчислити середньозважену величину, ви повинні спочатку помножити кожну статистичну інформацію на її вагу (або вагу), потім додати всі продукти й, нарешті, розділити зважену суму на суму всіх ваг.

Іншими словами, формула для середньозваженого має такий вигляд:

Де x _i представляє кожну вибірку даних, а w _i її відповідну вагу.

Таким чином, чим більшу вагу має частина даних, тим важливішою вона стає для розрахунку середньозваженого. Іншими словами, чим вище значення ваги для частини даних, тим більше це впливатиме на результат середньозваженого значення.

Середньозважене значення особливо корисне для обчислення оцінок, оскільки воно дає змогу з різною важливістю оцінювати вправи чи іспити, складені протягом курсу. Середньозважене значення також використовується для розрахунку ІСЦ (індексу споживчих цін), який є показником для вимірювання цін населення.

Крім зваженого середнього, існують також інші типи середніх, наприклад середнє геометричне, середнє арифметичне, середнє квадратичне та середнє гармонічне.

Як розрахувати середньозважену величину

Щоб розрахувати середньозважену величину, потрібно виконати наступні кроки:

Помножте кожну статистичну інформацію на її відповідну вагу.
Складіть усі продукти, розраховані на попередньому кроці.
Поділіть зважену суму вище на суму всіх ваг.
Отриманий результат є середньозваженим значенням статистичної вибірки.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити середньозважену величину будь-якого набору даних.

Приклад середньозваженого значення

Розглянувши визначення середнього зваженого, ми тепер розв’яжемо вправу, щоб повністю зрозуміти, як отримане середнє зважене з набору даних.

Учень 1-го курсу старшої школи отримав такі оцінки з математики: 7 за неповний іспит, який нараховує 30%, 9 за групову роботу, яка оцінюється 20%, 6 за вправи, які давалися на уроці зі зважуванням. 10% і 8 на підсумковому іспиті, який має вагу 40%. Яка ваша підсумкова оцінка з предмету?

Щоб визначити оцінку студента, необхідно знайти середньозважену величину із значеннями, наведеними твердженням. Для цього застосовуємо формулу середньозваженого:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

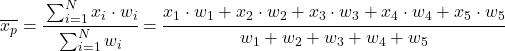
Оцінка кожного результату є статистичним значенням, і його відсоток відповідає вазі зазначеної вартості. Тому підставляємо значення і ваги в формулу і виконуємо розрахунок середньозваженого:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Отже, підсумкова оцінка з математики цього учня становитиме 7,7, оскільки це результат, отриманий із середньозваженого значення.

Калькулятор середньозваженого значення

Введіть дані з будь-якої статистичної вибірки та їх відповідні ваги в калькулятор нижче, щоб обчислити її середньозважену величину.

Введіть статистичні дані в перше поле та їх відповідні ваги в друге поле. Ви повинні записати ваги в тому ж порядку, що й дані, і в десятковому форматі. Усі числа мають бути розділені пробілом і введені крапкою як десятковим роздільником.

Стандартизовані ваги

Як ми бачили, у зваженому середньому вага – це значення, яке надається кожному фрагменту даних, щоб надати йому більшої чи меншої важливості. Отже, якщо інформація дуже важлива, вона матиме дуже велику вагу, але якщо інформація не дуже актуальна, вона матиме дуже низьку вагу.

Ну, нормалізована вага — це тип зважування, який використовується для отримання середнього зваженого значення без необхідності ділення.

Нормована вага — це вага елемента даних, поділена на суму всіх ваг.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Отже, сума всіх нормалізованих ваг дорівнює одиниці:

$\sum_{i=1}^N w_i'=1$

Отже, щоб обчислити середньозважену величину з нормалізованими вагами , просто помножте кожен елемент даних на його нормалізовану вагу:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

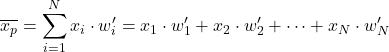
Наприклад, ми маємо статистичну вибірку, дані якої дорівнюють 24, 35, 17, 41, а їхні відповідні ваги — 4, 9, 6, 3. Щоб знайти середньозважене значення цього набору даних, ми можемо спочатку обчислити нормалізовані ваги, поділивши кожна вага на суму всіх ваг:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

А тепер просто помножте кожне з даних на його нормалізовану вагу, і результат буде середньозваженим:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Різниця між зваженим середнім і середнім арифметичним

Обчислення середньозваженого і середнього арифметичного проводиться однаково, оскільки необхідно виконувати схожі операції. При зваженому усередненні кожна точка даних множиться на її вагу та ділиться на суму ваг, але при арифметичному усередненні всі дані додаються разом і діляться на загальну кількість точок даних.

Різниця між зваженим середнім і середнім арифметичним полягає в його концепції, оскільки в середньому арифметичному вважається, що всі дані мають однакове значення, однак у зваженому середньому всі дані мають різну вагу.

Зауважте, що якщо всі ваги рівні, зважене середнє еквівалентне середньому арифметичному. Ви можете побачити математичний доказ нижче:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше