Корінь означає квадрат

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

Тут ми пояснюємо, що таке середнє квадратичне значення та як воно обчислюється. Крім того, ви дізнаєтесь про переваги та недоліки використання середнього та покрокового розв’язання вправи. Нарешті, ви зможете обчислити середнє квадратичне значення будь-якого набору даних за допомогою калькулятора в кінці статті.

Що таке середній квадрат?

Середнє квадратичне значення є мірою центральності описової статистики. Середнє квадратичне значення дорівнює квадратному кореню із середнього арифметичного з квадратів даних.

Середнє квадратичне значення також називають середньоквадратичним або середньоквадратичним .

Отже, формула для середнього квадратичного має такий вигляд:

Середнє квадратичне значення особливо корисно, коли статистична змінна приймає додатні та від’ємні значення, оскільки, зводячи кожен фрагмент даних у квадрат, усі значення стають додатними. Тому середній квадрат використовується для аналізу змінних, у яких важливий не знак, а його абсолютне значення.

Наприклад, середній квадрат використовується для вивчення похибок вимірювання, тому що в цих випадках ми не дивимося, додатна чи від’ємна похибка, а скоріше аналізуємо величину похибки під час вимірювання.

Крім того, квадрати великих чисел мають набагато вищі значення, ніж квадрати малих чисел, тому в середньому квадраті великі числа важливіші за малі.

Середнє квадратичне — це тип статистичного середнього разом із середнім арифметичним, середнім зваженим, середнім геометричним і середнім гармонічним.

Переваги та недоліки середньоквадратичного кореня

Квадратичне середнє має переваги та недоліки порівняно з іншими типами середніх.

Основна перевага квадратичного середнього полягає в тому, що воно дозволяє отримати дуже хорошу апроксимацію середнього значення дискретної змінної. З іншого боку, великим недоліком квадратичної середньої є те, що її розрахунок досить складний, оскільки необхідно виконати кілька операцій.

Навпаки, середньоквадратичний корінь дуже корисний для аналізу похибок вимірювань. Це також надає значно більшого значення високим значенням, хоча ця властивість означає, що неправильне вимірювання значно змінить середньоквадратичний результат.

Як розрахувати середнє квадратичне значення

Щоб обчислити середнє квадратичне значення, необхідно виконати наступні кроки:

Обчисліть квадрат кожного статистичного даних.
Складіть усі квадрати, розраховані на попередньому кроці.
Розділіть результат на кількість елементів даних у вибірці.
Знайдіть квадратний корінь із попереднього значення.
Отриманий результат є середнім квадратичним статистичної вибірки.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити середнє квадратичне значення будь-якого набору даних.

Середньоквадратичний приклад

Коли ми знаємо, як отримати середнє квадратичне значення, ми визначимо середнє квадратичне значення набору даних як приклад.

В університетській лабораторії професор просить своїх студентів провести експеримент із хімікатами. Мета хімічного досліду — отримати загальний об’єм розчину 3 л. Студентські групи отримали такі дані:

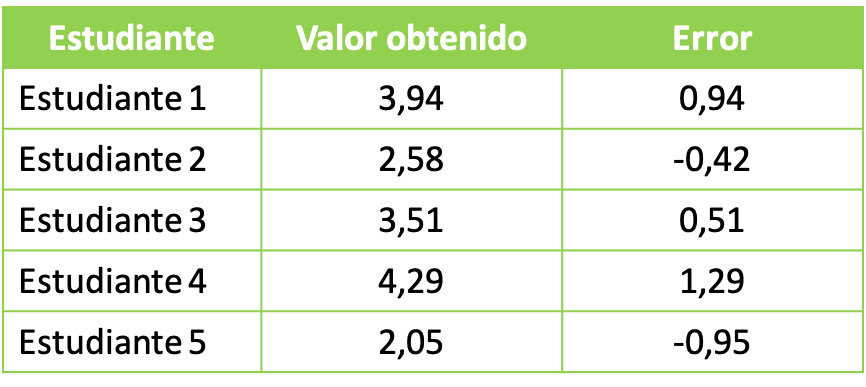
Для вивчення отриманих статистичних даних переходимо до розрахунку середньоквадратичного значення з похибкою, отриманою кожною групою. Тому ми застосовуємо формулу квадратичного середнього:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

І підставляємо дані у формулу і обчислюємо середнє квадратичне:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

Таким чином, середня похибка, отримана в досліді, за середнім квадратичним значенням становить 0,88 л.

Середньоквадратичний калькулятор

Введіть дані з будь-якої статистичної вибірки в наступний калькулятор, щоб обчислити її середнє квадратичне значення. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше