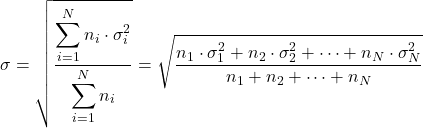Стандартне відхилення (або стандартне відхилення)

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке стандартне відхилення, яке також називають стандартним відхиленням. Ви дізнаєтесь, як розрахувати стандартне відхилення, покроковий практичний приклад і онлайн-калькулятор, щоб знайти стандартне відхилення будь-якої вибірки даних.

Що таке стандартне відхилення (або стандартне відхилення)?

Стандартне відхилення , яке також називають стандартним відхиленням , є мірою статистичної дисперсії. Іншими словами, стандартне відхилення – це значення, яке вказує на дисперсію набору статистичних даних.

Таким чином, стандартне відхилення (або стандартне відхилення) використовується для кількісного визначення дисперсії сукупності чи статистичної вибірки. Чим більше стандартне відхилення ряду даних, тим більше розсіяні дані. Інтерпретація також може бути виконана в іншому напрямку, якщо стандартне відхилення низьке, це означає, що загалом дані дуже близькі до свого середнього.

Під час обчислення стандартного або типового відхилення для сукупності символом стандартного відхилення є грецька літера сигма (σ). Але коли йдеться про стандартне відхилення вибірки, літера s використовується для позначення статистичного вимірювання.

У деяких книгах зі статистики та ймовірності стандартне відхилення також називають стандартним відхиленням.

Формула стандартного відхилення (або стандартного відхилення).

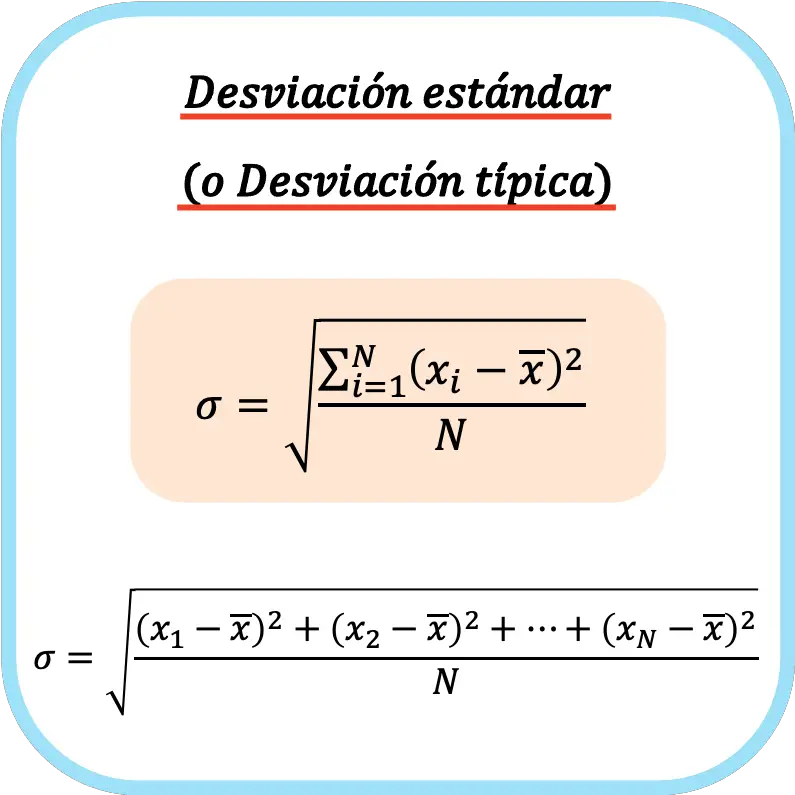
Стандартне відхилення (або стандартне відхилення) дорівнює кореню квадратному із суми квадратів відхилень ряду даних, поділеного на загальну кількість спостережень.

Таким чином , формула для обчислення стандартного відхилення (або стандартного відхилення) :

стандартное отклонение, стандартне відхилення

👉 Ви можете скористатися калькулятором нижче, щоб обчислити стандартне відхилення будь-якого набору даних.

Підсумовуючи, щоб знайти стандартне відхилення набору даних, вам потрібно обчислити всі відхилення (визначені як різниця між точкою даних і середнім арифметичним), збільшити відхилення до двох, додати їх усі, а потім розділити на всього кількість даних і, нарешті, витягніть квадратний корінь.

Приклад стандартного відхилення (або стандартного відхилення)

Розглядаючи визначення стандартного відхилення (або типового відхилення), нижче наведено покроковий приклад, щоб ви могли побачити, як обчислюється стандартне відхилення ряду даних.

Обчисліть стандартне відхилення таких значень: 3, 6, 2, 9, 4.

Перше, що нам потрібно зробити, це визначити вибіркове середнє. Для цього ми складаємо всі дані і ділимо на загальну кількість спостережень, тобто п’ять:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Тепер ми використовуємо формулу стандартного відхилення:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Підставляємо дані у формулу:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

І, нарешті, обчислюємо стандартне відхилення:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Калькулятор стандартного відхилення (або стандартного відхилення).

Введіть набір статистичних даних у наступний онлайн-калькулятор, щоб обчислити його стандартне відхилення (або стандартне відхилення). Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Стандартне (або типове) відхилення для згрупованих даних

Щоб обчислити стандартне відхилення (або стандартне відхилення) даних, згрупованих в інтервали , потрібно виконати наступні кроки:

Знайдіть середнє значення згрупованих даних.
Розрахувати відхилення згрупованих даних.
Зведіть кожен проміжок у квадрат.
Помножте кожен попередній результат на частоту його інтервалу.
Складіть суму всіх значень, отриманих на попередньому кроці.
Розділіть на загальну кількість спостережень.
Візьміть квадратний корінь із попереднього значення. Отримане число є стандартним відхиленням згрупованих даних.

На завершення формула для обчислення стандартного відхилення даних, згрупованих в інтервали, виглядає так:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

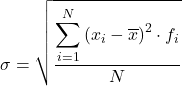
Хоча наведена вище формула зазвичай використовується, наступний алгебраїчний вираз також може бути використаний, оскільки отримано той самий результат:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

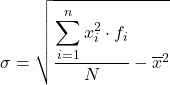
Щоб ви могли побачити, як це робиться, нижче наведено покрокову вправу на стандартне відхилення даних, згрупованих у інтервали. Точніше, буде розраховано стандартне відхилення наступних статистичних даних:

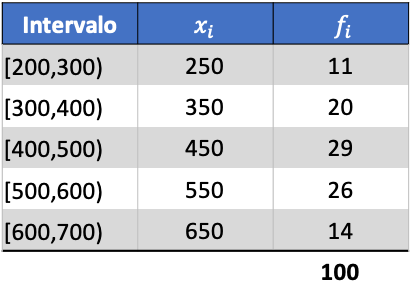
Спочатку ми множимо оцінку класу кожного інтервалу на його частоту, щоб обчислити середнє арифметичне:

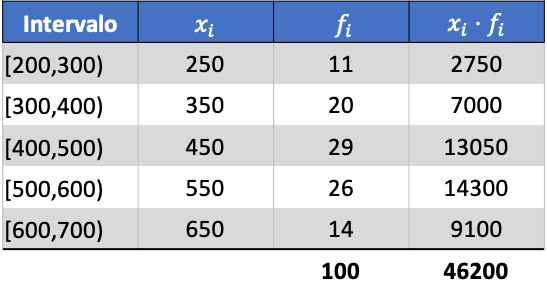
Отже, середнє значення згрупованих даних буде:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

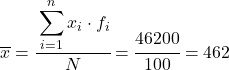
Тепер, коли ми знаємо середнє значення, нам потрібно додати наступні три стовпці до таблиці даних:

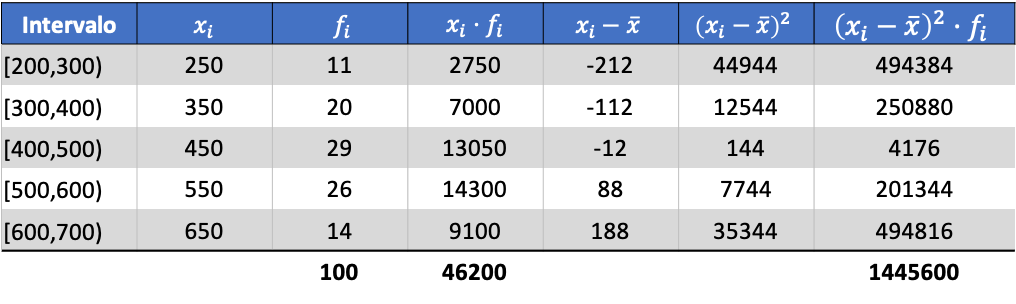
розв’язана вправа стандартного відхилення або стандартного відхилення для згрупованих даних

Тоді стандартне відхилення згрупованих даних буде результатом квадратного кореня із підсумку останнього стовпця, поділеного на загальну кількість спостережень:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

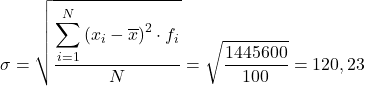
Стандартне (або типове) відхилення та дисперсія

Зв’язок між стандартним відхиленням (або типовим відхиленням) і дисперсією полягає в тому, що стандартне відхилення є квадратним коренем із дисперсії.

Отже, якщо ми знаємо значення дисперсії набору даних, ми можемо легко обчислити стандартне відхилення, витягнувши квадратний корінь. Або навпаки, якщо ми знаємо стандартне відхилення, ми можемо знайти дисперсію, звівши значення в квадрат.

$Var(X)=\sigma^2$

Насправді дисперсію можна представити просто за допомогою символу квадрата стандартного відхилення. Таким чином, символ дисперсії генеральної сукупності є сигма-квадратом (σ ² ), а символом дисперсії вибірки є s квадрат (s ² ).

Крім того, поняття стандартного відхилення та дисперсії мають однакове тлумачення, оскільки обидва показують дисперсію серії статистичних даних.

Властивості стандартного відхилення (або стандартного відхилення)

Стандартне відхилення має такі властивості:

Стандартне відхилення вибірки даних не може бути негативним.

$\sigma \ge 0$

Стандартне відхилення дорівнюватиме нулю, якщо всі дані однакові.

$\sigma =0$

Якщо до всіх даних додати постійний термін, значення стандартного відхилення не зміниться.

$\sigma (X+k)=\sigma (X)$

Якщо всі дані помножити на число, стандартне відхилення буде помножено на абсолютне значення цього числа.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

Стандартне відхилення суми двох випадкових змінних дорівнює квадратному кореню із суми дисперсій змінних плюс подвоєна коваріація між двома змінними.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Якщо ми знаємо стандартні відхилення різних розподілів (σ _i ) і їх кількість даних (n _i ), ми можемо обчислити загальне стандартне відхилення, застосувавши таку формулу:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше