Частота (статистика)

У цій статті пояснюється, що таке поняття частоти в статистиці. Таким чином, ви знайдете визначення частоти в статистиці, різні типи частот, які існують, і, нарешті, як створити таблицю частот.

Що таке частота в статистиці?

У статистиці частота – це кількість разів, коли значення з’являється в наборі даних. Простіше кажучи, частота — це кількість повторів значення в статистичній вибірці.

Наприклад, якщо в опитуванні п’ять людей відповіли, що їхній улюблений колір – синій, то частота синього кольору дорівнює 5.

Як правило, у статистиці літера f з індексом i використовується для представлення частоти значення i , тому символ частоти є _fi .

Сума всіх частот дає загальну кількість даних у вибірці. Тому наступна формула завжди справедлива для будь-якого статистичного дослідження:

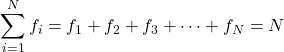
золото

це частота значення

І

– загальна кількість спостережень.

Типи частот у статистиці

У статистиці різні типи частот такі:

• Абсолютна частота : відповідає кількості разів, коли значення з’являється в статистичній вибірці.
• Кумулятивна абсолютна частота : обчислюється додаванням абсолютної частоти значення плюс абсолютні частоти всіх менших значень.
• Відносна частота : це абсолютна частота, поділена на загальну кількість даних.
• Кумулятивна відносна частота : дорівнює сумі відносної частоти значення плюс відносні частоти всіх нижчих значень.

У розділі нижче ви можете побачити, як обчислюється кожен тип частоти.

Таблиця частот

Зазвичай у статистиці розрахунки частот вибірки даних підсумовуються в таблиці частот. Нижче наведено покроковий приклад, щоб ви могли побачити, як це зробити.

• Оцінки, отримані з предмету статистика у класі, який налічує 30 учнів, такі. Побудуйте частотну таблицю набору даних.

Оскільки всі числа можуть бути лише цілими, це дискретна змінна. Тому немає необхідності групувати дані в інтервали.

Тому нам потрібно побудувати таблицю, у якій кожне значення буде рядком. Крім того, нам потрібно знайти абсолютну частоту кожного значення, для цього просто підрахуйте, скільки разів значення з’являється у вибірці даних.

Зверніть увагу, що сума всіх абсолютних частот дорівнює загальній кількості даних. Якщо це правило не дотримується, це означає, що ви забули надати певну інформацію.

Тепер, коли ми знаємо абсолютну частоту, нам потрібно знайти сукупну абсолютну частоту. Для цього розрахунку у нас є два варіанти: або ми додаємо абсолютну частоту значення плюс усі абсолютні частоти найменших значень, або, навпаки, ми додаємо абсолютну частоту значення плюс кумулятивну абсолютну частоту попереднього значення.

Кумулятивна абсолютна частота останнього значення завжди відповідає загальній кількості даних, ви можете скористатися цим трюком, щоб переконатися, що обчислення правильні.

Далі нам потрібно визначити відносну частоту, яка обчислюється діленням абсолютної частоти на загальну кількість точок даних (30):

Майте на увазі, що сума всіх відносних частот завжди дорівнює 1, інакше це означає, що деякі розрахунки в таблиці частот неправильні.

Нарешті, достатньо витягти накопичену відносну частоту. Щоб зробити це, ви повинні додати відносну частоту відповідного значення плюс усі попередні відносні частоти або, що дорівнює тому ж самому, попередню накопичену відносну частоту:

Коротко кажучи, частотна таблиця з усіма частотами проблемних даних виглядає наступним чином: