Мода (статистика)

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке режим у статистиці. Ви дізнаєтеся, як знайти статистичний режим для згрупованих і незгрупованих даних, різні типи режимів і кілька прикладів цього статистичного вимірювання.

Що таке режим у статистиці?

У статистиці мода — це значення в наборі даних, яке має найвищу абсолютну частоту, тобто мода — це найбільш повторюване значення в наборі даних.

Тому, щоб обчислити режим набору статистичних даних, просто підрахуйте, скільки разів кожен елемент даних з’являється у вибірці, і найбільш повторювані дані будуть режимом.

Режим використовується для визначення статистичного розподілу, оскільки найбільше повторюване значення зазвичай знаходиться в центрі розподілу.

Режим також можна назвати статистичним режимом або модальним значенням . Так само, коли дані групуються в інтервали, найбільш повторюваний інтервал є модальним інтервалом або модальним класом .

Загалом, термін Mo використовується як символ для статистичного режиму, наприклад, режим розподілу X є Mo(X).

Майте на увазі, що мода є статистичним показником положення центру, а також медіани та середнього значення. Нижче ми побачимо значення кожного з цих статистичних показників.

Типи режимів у статистиці

У статистиці існує кілька типів режимів, які класифікуються за кількістю найбільш повторюваних значень:

Унімодальний режим : є лише одне значення з максимальною кількістю повторів. Наприклад, [1, 4, 2, 4, 5, 3].
Бімодальний режим : максимальна кількість повторів відбувається при двох різних значеннях, і обидва значення повторюються однакову кількість разів. Наприклад, [2, 6, 7, 2, 3, 6, 9].
Мультимодальний режим : три або більше значень мають однакову максимальну кількість повторень. Наприклад, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].

Як знайти статистичний режим

Щоб знайти статистичний режим набору даних, ви повинні виконати такі дії:

Впорядкуйте дані. Цей крок не є обов’язковим, але він полегшить підрахунок чисел.
Порахуйте, скільки разів з’являється кожне число.
Число, яке з’являється найчастіше, є статистичним режимом.

Приклади статистичного режиму

Розглядаючи визначення моди в статистиці, нижче ви можете побачити приклади кожного типу моди, щоб ви могли краще зрозуміти концепцію.

Приклад унімодального режиму

Який режим наступного набору даних?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

Номери не впорядковані, тому спочатку впорядкуємо їх, щоб легше було знайти режим.

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

Числа 2 і 9 з’являються двічі, але число 5 повторюється тричі. Таким чином, режим ряду даних номер 5.

$Mo=5$

Приклад бімодального режиму

Обчисліть моду наступного набору даних:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

Спочатку впорядкуємо числа:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

Як ви бачите, число 6 і число 8 з’являються чотири рази, що є максимальною кількістю повторень. Тому в цьому випадку це бімодальний режим, а два числа є режимом набору даних:

$Mo=\{ 6 \ ; \ 8\}$

Приклад мультимодального режиму

Знайдіть такий режим набору даних:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

Оскільки даних багато, ми спочатку відсортуємо їх у порядку зростання, щоб було легше підрахувати:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

Найчастіше повторюються числа 20, 27 і 31, всі три числа повторюються п’ять разів. Тому режим цього прикладу є мультимодальним.

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

модний калькулятор

Введіть дані з будь-якої статистичної вибірки в наступний онлайн-калькулятор, щоб розрахувати її режим. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Режим для згрупованих даних

Коли ми маємо дані, згруповані у вигляді інтервалів, ми насправді не знаємо, скільки разів повторюється кожна частина даних, ми знаємо лише частоту кожного інтервалу.

Таким чином, щоб обчислити режим даних, згрупованих в інтервали, ми повинні використовувати таку формулу :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

золото:

L _i – нижня межа модального інтервалу (найвищий абсолютний частотний інтервал).
f _i – абсолютна частота модального інтервалу.
f _i-1 – абсолютна частота інтервалу перед модальним.
f _i+1 – абсолютна частота інтервалу після модального.
A _i – ширина модального інтервалу.

Як приклад, нижче ви розв’язали вправу, у якій обчислюється режим даних, згрупованих у інтервали:

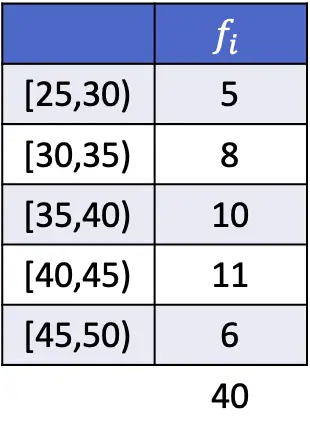
приклад статистичного режиму для згрупованих даних

У цьому випадку модальний інтервал дорівнює [40,45), оскільки це інтервал з найбільшою абсолютною частотою. Отже, параметри формули режиму для згрупованих даних такі:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

Тому ми застосовуємо формулу для визначення режиму даних, згрупованих в інтервали, і виконуємо обчислення:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

Різниця між модою, середнім і медіаною

У цьому останньому розділі ми побачимо різницю між модою, середнім і медіаною. Оскільки всі три є статистичними показниками центральної позиції, їхнє значення різне.

Як пояснюється в цій статті, мода в математиці – це значення, яке найчастіше повторюється в наборі даних.

По-друге, середнє – це середнє значення всіх статистичних даних. Таким чином, щоб отримати середнє значення певних даних, ви повинні скласти всі дані, а потім розділити результат на кількість спостережень.

І, нарешті, медіана – це значення, яке займає центральне положення, коли дані впорядковані.

Таким чином, три статистичні показники допомагають визначити розподіл ймовірностей, оскільки вони дають уявлення про його центральні значення. Але майте на увазі, що немає жодного показника, який би був кращим за інший, вони просто означають різні поняття.

Модні властивості

Модними властивостями є:

Моду можна знайти як у кількісних змінних, так і в якісних змінних.
Якщо застосувати лінійне перетворення до випадкової величини, значення середнього змінюватиметься залежно від застосованих операцій.

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

Загалом режим нечутливий до викидів.
Якщо всі значення мають однакову частоту, режиму немає.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше