Кореляції в stata: пірсон, спірмен і кендалл

У статистиці кореляція означає силу та напрямок зв’язку між двома змінними. Значення коефіцієнта кореляції може коливатися від -1 до 1, де -1 вказує на ідеальний негативний зв’язок, 0 вказує на відсутність зв’язку, а 1 вказує на ідеальний позитивний зв’язок.

Існує три поширених способи вимірювання кореляції:

Кореляція Пірсона: використовується для вимірювання кореляції між двома безперервними змінними. (наприклад, зріст і вага)

Кореляція Спірмена: використовується для вимірювання кореляції між двома класифікованими змінними. (наприклад, рейтинг результатів іспиту з математики учня порівняно з рейтингом результатів іспиту з природничих наук у класі)

Кореляція Кендалла: використовується, коли потрібно використовувати кореляцію Спірмена, але розмір вибірки невеликий і існує багато пов’язаних рейтингів.

Цей посібник пояснює, як знайти три типи кореляцій у Stata.

Завантаження даних

Для кожного з наступних прикладів ми будемо використовувати набір даних під назвою auto . Ви можете завантажити цей набір даних, ввівши наступне в поле команди:

використовуйте https://www.stata-press.com/data/r13/auto

Ми можемо отримати швидкий огляд набору даних, ввівши наступне в полі команди:

узагальнити

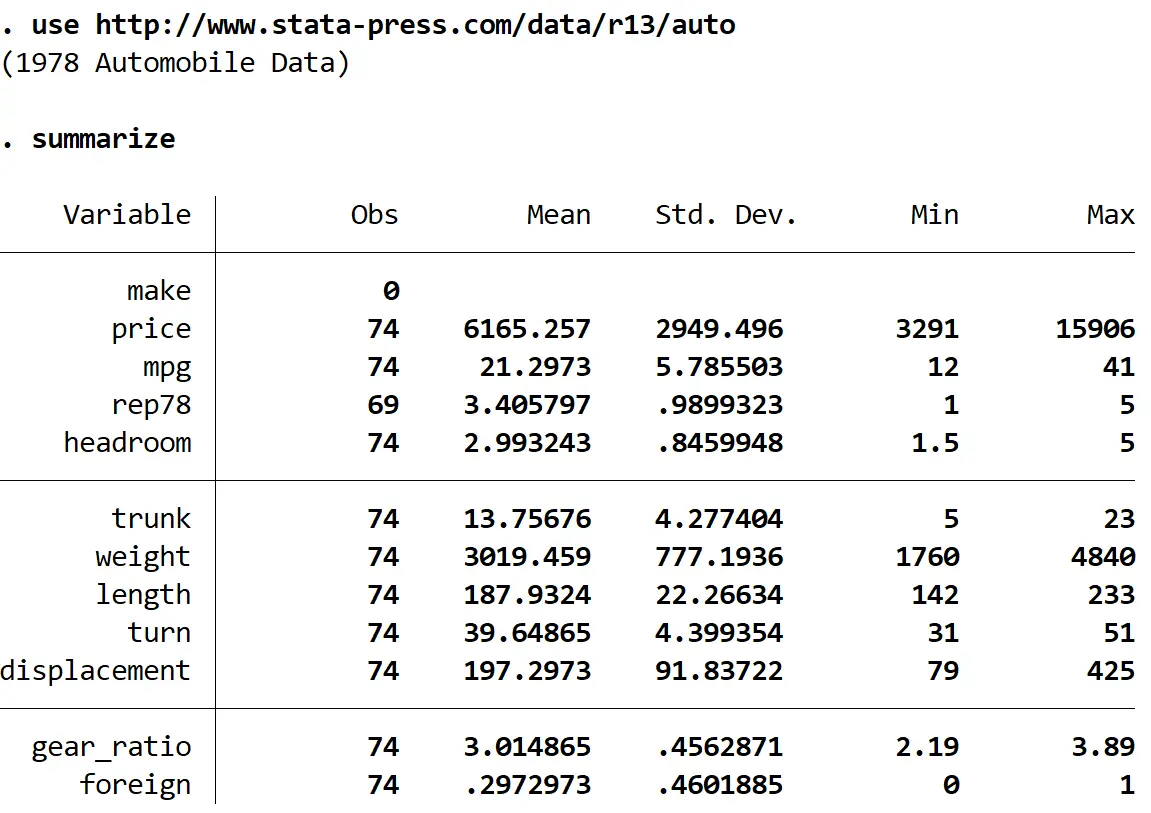
Ми бачимо, що всього в наборі даних 12 змінних.

Як знайти кореляцію Пірсона в Stata

Ми можемо знайти коефіцієнт кореляції Пірсона між змінними ваги та довжини за допомогою команди pwcorr :

довжина ваги pwcorr

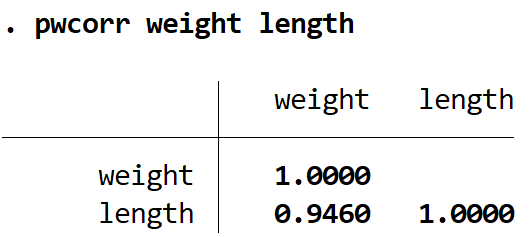
Коефіцієнт кореляції Пірсона між цими двома змінними становить 0,9460 . Щоб визначити, чи є цей коефіцієнт кореляції значущим, ми можемо знайти значення p за допомогою команди sig :

pwcorr маса довжина, сиг

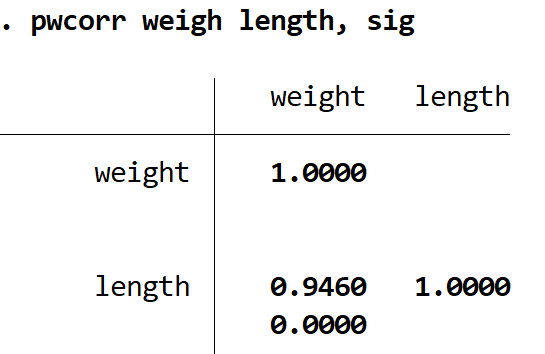
P-значення дорівнює 0,000 . Оскільки це значення менше 0,05, кореляція між цими двома змінними є статистично значущою.

Щоб знайти коефіцієнт кореляції Пірсона для кількох змінних, просто введіть список змінних після команди pwcorr :

pwcorr вага довжина водотоннажність, сиг

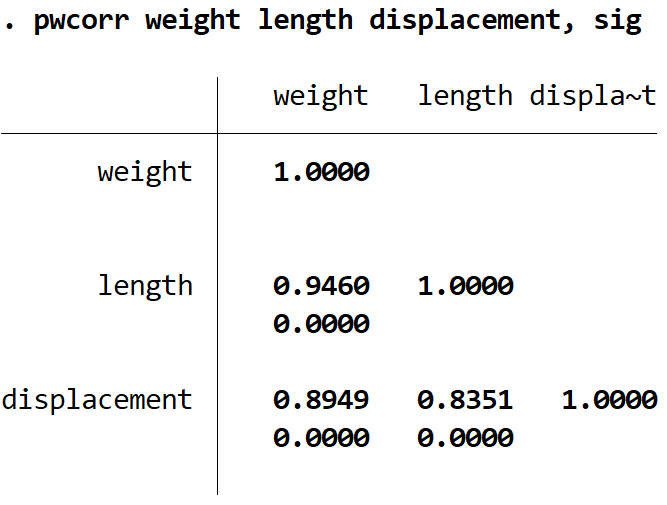
Ось як інтерпретувати результат:

• Кореляція Пірсона між вагою та довжиною = 0,9460 | р-значення = 0,000
• Кореляція Пірсона між вагою та об’ємом = 0,8949 | р-значення = 0,000
• Кореляція Пірсона між переміщенням і довжиною = 0,8351 | р-значення = 0,000

Як знайти кореляцію Спірмена в Stata

Ми можемо знайти коефіцієнт кореляції Спірмена між змінними trunk і rep78 за допомогою команди spearman :

копія стовбура rep78

Ось як інтерпретувати результат:

• Кількість спостережень: це кількість попарних спостережень, які використовуються для обчислення коефіцієнта кореляції Спірмена. Оскільки для змінної rep78 були відсутні деякі значення, Stata використовувала лише 69 спостережень на пару (замість повних 74).
• Ро Спірмена: це коефіцієнт кореляції Спірмена. У цьому випадку це -0,2235, що вказує на наявність негативної кореляції між двома змінними. Коли один збільшується, інший має тенденцію до зменшення.
• Імовірність > |t| : це p-значення, пов’язане з перевіркою гіпотези. У цьому випадку p-значення становить 0,0649, що вказує на відсутність статистично значущої кореляції між двома змінними при α = 0,05.

Ми можемо знайти коефіцієнт кореляції Спірмена для кількох змінних, просто ввівши більше змінних після команди Спірмена . Ми можемо знайти коефіцієнт кореляції та відповідне значення p для кожної попарної кореляції за допомогою команди stats(rho p) :

spearman trunk rep78 gear_ratio, статистика (rho p)

Ось як інтерпретувати результат:

• Кореляція Спірмена між тулубом і реп78 = -0,2235 | р-значення = 0,0649
• Кореляція Спірмена між стовбуром і передавальним числом = -0,5187 | р-значення = 0,0000
• Кореляція Спірмена між gear_ratio і rep78 = 0,4275 | р-значення = 0,0002

Як знайти кореляцію Кендалла в Stata

Ми можемо знайти коефіцієнт кореляції Кендалла між змінними trunk і rep78 за допомогою команди ktau :

ktau trunk rep78

Ось як інтерпретувати результат:

• Кількість спостережень: це кількість попарних спостережень, використаних для обчислення коефіцієнта кореляції Кендалла. Оскільки для змінної rep78 були відсутні деякі значення, Stata використовувала лише 69 спостережень на пару (замість повних 74).
• Tau-b Кендалла: це коефіцієнт кореляції Кендалла між двома змінними. Зазвичай ми використовуємо це значення замість tau-a, тому що tau-b вносить коригування у випадку рівності. У цьому випадку tau-b = -0,1752, що вказує на негативну кореляцію між двома змінними.
• Можливість > |z| : це p-значення, пов’язане з перевіркою гіпотези. У цьому випадку p-значення становить 0,0662, що вказує на відсутність статистично значущої кореляції між двома змінними при α = 0,05.

Ми можемо знайти коефіцієнт кореляції Кендалла для кількох змінних, просто ввівши більше змінних після команди ktau . Ми можемо знайти коефіцієнт кореляції та відповідне значення p для кожної попарної кореляції за допомогою команди stats(taub p) :

ktau trunk rep78 gear_ratio, статистика (taub p)

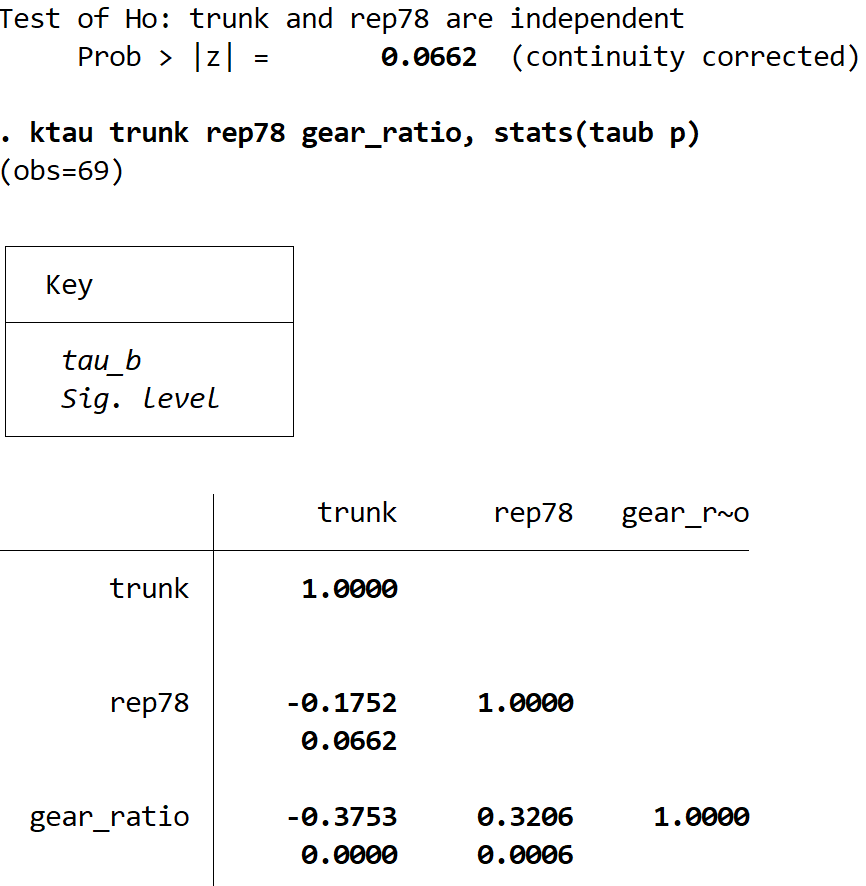
• Кореляція Кендалла між тулубом і реп78 = -0,1752 | p-значення = 0,0662
• Кореляція Кендалла між тулубом і передавальним числом = -0,3753 | р-значення = 0,0000
• Кореляція Кендалла між gear_ratio і rep78 = 0,3206 | р-значення = 0,0006