Стратифікована вибірка

за Редакція 6 Серпня, 2023 Статистика 0 коментарів

У цій статті ми пояснюємо, що таке стратифікована вибірка та як вона здійснюється. Тут ви знайдете пояснення підтипів стратифікованої вибірки та, нарешті, переваги та недоліки стратифікованої вибірки.

Що таке стратифікована вибірка?

Стратифікована вибірка — це статистичний метод, який використовується для відбору елементів вибірки шляхом поділу сукупності на групи (так звані страти). Тобто при стратифікованій вибірці популяція поділяється на страти, і особи з кожної страти відбираються випадковим чином для формування всієї досліджуваної вибірки.

Страти — це однорідні групи, або, іншими словами, індивіди в страті мають власні характеристики, які відрізняють їх від інших страт. Тому людина може належати лише до однієї верстви.

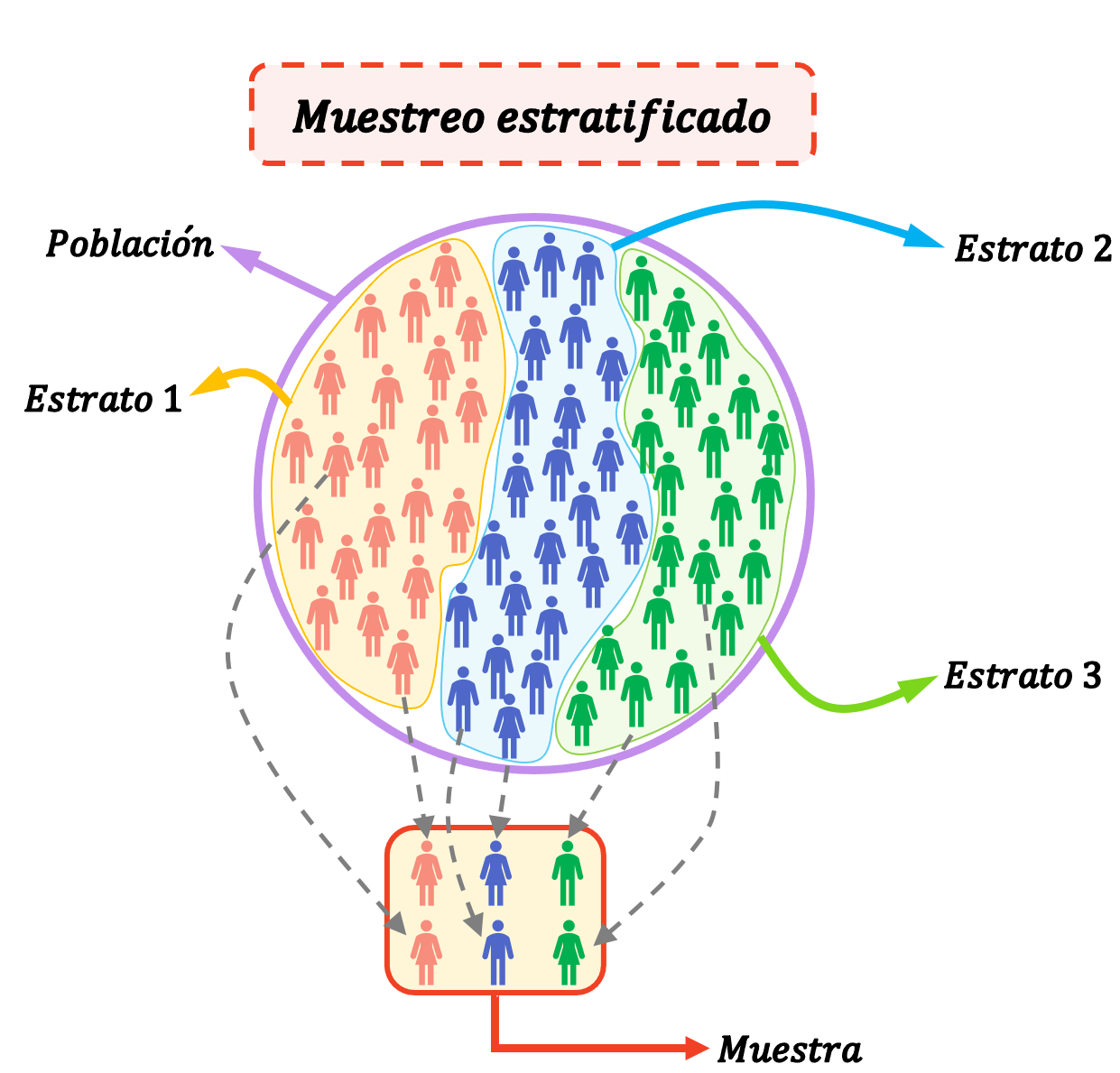
Стратифікована вибірка дуже корисна, коли сукупність складається з дуже однорідних груп, які сильно відрізняються одна від одної.

Логічно сума розміру всіх страт дає розмір статистичної сукупності:

$N=N_1+N_2+N_3+\dots+N_k$

Подібним чином сума розміру вибірки, обраної в кожній страті, дорівнює загальному розміру вибірки статистичного дослідження:

$n=n_1+n_2+n_3+\dots+n_k$

Зазвичай ми розрізняємо великі та малі літери для позначення сукупності чи вибірки відповідно.

Як зробити стратифіковану вибірку

Кроки виконання стратифікованої вибірки такі:

Визначте цільову групу населення.
Виберіть змінну стратифікацію та кількість страт.
Визначте , до якого прошарку належить кожен елемент сукупності.
Обчисліть розмір кожної страти , яка буде частиною вибірки.
Випадково виберіть елементи з кожної страти , які належатимуть до досліджуваної вибірки. Для кожного шару потрібно вибрати стільки елементів, скільки було вирішено на попередньому кроці.

Пам’ятайте, що розмір кожної страти у вибірці залежить не лише від розміру страти, але й від типу стратифікованої вибірки. Далі пояснюється кожен тип стратифікованої вибірки та пояснюється, як на прикладі обчислюється розмір вибірки для кожної страти.

Типи стратифікованої вибірки

Тепер, коли ви знаєте визначення стратифікованої вибірки, ви повинні знати, що існує кілька типів стратифікованої вибірки, які класифікуються таким чином:

Пропорційна стратифікована вибірка
Рівномірна стратифікована вибірка
Вибірка оптимальна

Кожен тип стратифікованої вибірки докладно пояснюється нижче, щоб краще зрозуміти значення кожного з них.

Пропорційна стратифікована вибірка

У стратифікованій пропорційній вибірці або вибірці з пропорційним розподілом кількість елементів із кожної страти, які є частиною досліджуваної вибірки, пропорційна розміру кожної страти.

Таким чином, якщо одна страта більша за іншу, кінцева вибірка міститиме більше елементів із цієї страти. З іншого боку, якщо одна страта менша за іншу, у вибірці статистичного аналізу буде менше елементів із цієї страти.

Цей тип стратифікованої вибірки корисний, коли страти мають різні розміри, і ми хочемо, щоб вибірка включала більше елементів із більших страт.

Щоб обчислити кількість елементів з кожної страти , яка буде у вибірці, розмір кожної страти потрібно розділити на суму розмірів усіх страт. Результатом буде частка страти, яку слід включити до вибірки, тому її потрібно буде помножити на бажаний розмір вибірки.

$n_i=n\cdot \cfrac{N_i}{N_1+N_2+\dots +N_k}=n\cdot \cfrac{N_i}{N}$

золото

$n$

бажаний загальний розмір вибірки,

$n_i$

кількість елементів у пласті

$i$

для включення до вибірки,

$N_i$

розмір пласта

$i$

, І

$N$

загальна кількість елементів у популяції.

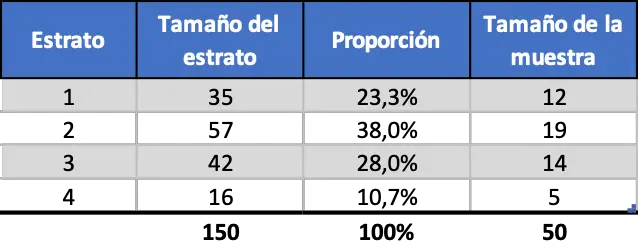
Наприклад, уявіть, що ми хочемо провести дослідження в компанії зі 150 працівниками, взявши вибірку з 50 осіб і розділивши дані на основі віку працівників. Ми можемо класифікувати дані наступним чином:

Від 20 до 29 років: 35 робітників
Від 30 до 39 років: 57 працівників
Від 40 до 49 років: 42 працівники
Від 50 до 59 років: 16 працівників

Таким чином, якщо ми пропорційно стратифікуємо дані, вибірка буде такою:

Рівномірна стратифікована вибірка

У рівномірній стратифікованій вибірці або рівномірній вибірці афіксації кількість елементів з кожної страти, які входять до досліджуваної вибірки, однакова.

Тому кожна страта має однакову вагу в цьому типі вибірки. Незалежно від того, чи має страта більше чи менше осіб, ніж інша страта, усі вони будуть представлені у вибірці однаковою кількістю осіб.

У цьому випадку, щоб обчислити розмір елементів у кожній страті, бажаний розмір вибірки необхідно розділити на кількість існуючих страт. Іншими словами, слід використовувати таку формулу:

$n_i=\cfrac{n}{k}$

золото

$n$

бажаний загальний розмір вибірки,

$n_i$

кількість елементів у пласті

$i$

хто буде включений до вибірки, і

$k$

кількість верств, на які поділили населення.

Дотримуючись попереднього прикладу, оскільки нам потрібна вибірка з 50 працівників і загалом було 4 різні страти, розмір вибірки для кожної страти буде:

$n_i=\cfrac{50}{4}=12,5$

Результат є десятковим числом, одні страти матимуть 12 працівників, а інші 13, поки не досягнуть 50 працівників. Отже, рівномірна стратифікована вибірка виглядає наступним чином:

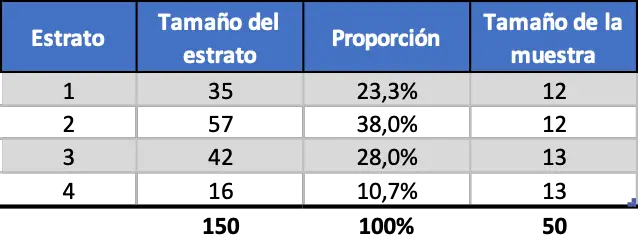
Як ви бачите, розмір вибірки кожної страти не залежить від частки кожного.

Оптимальна стратифікована вибірка

При оптимальній стратифікованій вибірці кількість елементів у кожній страті залежить пропорційно від мінливості кожної страти.

Таким чином, страти з більшою мінливістю матимуть більший розмір вибірки, і навпаки, страти з меншою мінливістю матимуть менший розмір вибірки.

Формула для визначення кількості елементів із кожної страти буде частиною вибірки статистичного дослідження така:

$n_i=n\cdot \cfrac{\sigma_i\cdot N_i}{\displaystyle \sum_{j=1}^k \sigma_j\cdot N_j }$

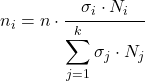
золото

$n$

бажаний загальний розмір вибірки,

$n_i$

– кількість елементів у страті

$i$

для включення до вибірки,

$\sigma_i$

є стандартним відхиленням (або типовим відхиленням) страти

$i$

, І

$N_i$

— розмір пласта

$i$

Переваги та недоліки стратифікованої вибірки

Стратифікована вибірка має такі переваги та недоліки:

перевага	Недоліки
Це дає можливість статистично досліджувати не тільки все населення, а й кожну окрему прошарок.	Це складний метод вибірки для реалізації.
Помилка вибірки, допущена стратифікованою вибіркою, завжди дорівнює або менше, ніж помилка простої випадкової вибірки.	Це трудомісткий і, отже, дорогий процес відбору проб.
Він дозволяє скористатися знаннями дослідника про населення.	Необхідно багато інформації про аналізовану пробу, щоб мати можливість її стратифікувати.
За допомогою стратифікованої вибірки ми гарантуємо, що принаймні один елемент із кожної страти включено до вибірки.	Необхідно знати частку кожної страти, щоб мати можливість провести вибірку.

Основною характеристикою стратифікованої вибірки є те, що вона використовується для статистичного аналізу кожної групи або страти, на яку було поділено сукупність. Звичайно, за допомогою цього типу вибірки також можна досліджувати всю сукупність. Крім того, переваги стратифікації даних будуть більшими, якщо страти відрізнятимуться один від одного.

Навпаки, факт стратифікації даних для здійснення вибірки передбачає збільшення складності вибірки, стратифіковану вибірку складніше проводити порівняно з іншими типами вибірки. Ця властивість також означає, що виготовлення зразка є дорогим, оскільки для правильного розшарування потрібен час.

Іншим недоліком стратифікованої вибірки є те, що вона вимагає великої кількості інформації про генеральну сукупність, яку потрібно вивчити, що не є необхідним для інших типів вибірки, наприклад простої випадкової вибірки. Хоча цей недолік можна пом’якшити, якщо дослідник має великі знання в цій галузі.

Нарешті, за допомогою стратифікованої вибірки ми отримуємо вибірку, яка є більш репрезентативною для генеральної сукупності, ніж в інших типах вибірки, оскільки ми забезпечуємо включення елементів із кожної страти. Навпаки, в інших зразках результуюча вибірка може не містити елементів із жодної страти.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке стратифікована вибірка?

Як зробити стратифіковану вибірку

Типи стратифікованої вибірки

Пропорційна стратифікована вибірка

Рівномірна стратифікована вибірка

Оптимальна стратифікована вибірка

Переваги та недоліки стратифікованої вибірки

Про автора

Редакція

Додати коментар