Теорема чебишева

за Редакція 5 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке теорема Чебишева. Тут ви знайдете формулу теореми Чебишева, розв’язану вправу та, крім того, онлайн-калькулятор теореми Чебишева. Нарешті, це показує різницю між теоремою Чебишева та емпіричним правилом.

Що таке теорема Чебишева?

Теорема Чебишева , також відома як нерівність Чебишева , — це статистичне правило, яке використовується для обчислення ймовірності того, що значення випадкової величини лежить на певній відстані від свого середнього.

Іншими словами, у статистиці теорема Чебишева використовується для визначення ймовірності того, що значення знаходиться в межах довірчого інтервалу.

Крім того, теорема Чебишева також використовується для доведення інших статистичних теорем, таких як закон великих чисел.

Хоча теорема Чебишева була вперше сформульована французом Ірене-Жюлем Бієнайме, теорема названа так тому, що її створив росіянин Пафнутій Чебушев у 1867 році.

Формула теореми Чебишева

Теорема Чебишева говорить, що ймовірність того, що значення дорівнює k стандартним відхиленням від середнього, більше або дорівнює одиниці мінус відношення одиниці до k у квадраті.

Тому формула теореми Чебишева має такий вигляд:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\geq 1 -\frac{1}{k^2}$

золото

$X$

– значення випадкової величини,

$\mu$

середнє арифметичне змінної,

$\sigma$

його стандартне відхилення і

$k$

кількість стандартних відхилень від середнього, за якими має бути обчислена ймовірність.

Зауважте, що цю формулу можна використовувати, лише якщо кількість стандартних відхилень, на основі яких виконується розрахунок, перевищує 1, або іншими словами, якщо k більше за 1.

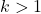$k>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”41″ style=”vertical-align: -2px;”></p> </p> <p> 👉 <u style=$ Щоб обчислити ймовірність, ви можете скористатися онлайн-калькулятором теореми Чебишева нижче.

Приклад теореми Чебишева

Після того, як ми побачили визначення теореми Чебишева та її формулу, ось розв’язаний приклад цієї статистичної теореми, щоб краще зрозуміти концепцію.

Якщо оцінки, отримані в статистиці курсу університету, визначаються розподілом із середнім значенням 65 і стандартним відхиленням 10, який відсоток студентів отримав оцінку від 50 до 80?

Для вирішення цієї задачі потрібно застосувати формулу теореми Чебишева. Однак спочатку ми повинні визначити, скільки стандартних відхилень мають значення 50 і 80 від середнього значення змінної, для цього нам просто потрібно зробити наступний розрахунок:

$k=\cfrac{\text{valor}-\text{media}}{\text{desviaci\'on t\'ipica}}$

$k=\cfrac{50-65}{10}=-1,5$

$k=\cfrac{80-65}{10}=1,5$

Тому значення 50 і 80 відповідають 1,5 стандартним відхиленням від нижнього і верхнього середнього відповідно. Тому використаємо формулу теореми Чебишевої з k=1,5:

$\displaystyle P(\mu-k\sigma\leq X \leq \mu+k\sigma)\leq 1 -\frac{1}{k^2}$

$\displaystyle P(\mu-1,5\sigma\leq X \leq \mu+1,5\sigma)\leq 1 -\frac{1}{1,5^2}$

$\displaystyle P(50\leq X \leq 80)\leq 0,5556$

Таким чином, принаймні 55,56% студентів отримали оцінку від 50 до 80.

Калькулятор теореми Чебишева

Введіть число стандартних відхилень між значеннями, про які йде мова, і середнім (k) , а потім натисніть «Обчислити». Потім калькулятор поверне мінімальну ймовірність довірчого інтервалу.

Ви повинні ввести кількість стандартних відхилень, використовуючи крапку як десятковий роздільник.

Теорема і емпіричне правило Чебишева

Двома тісно пов’язаними поняттями в статистиці є теорема Чебишева та емпіричне правило, оскільки обидва використовуються для обчислення ймовірності довірчих інтервалів.

Різниця між теоремою Чебишева та емпіричним правилом полягає в тому, що теорему Чебишева можна використовувати для будь-якого типу розподілу, тоді як емпіричне правило дійсне лише для нормального розподілу.

Тому використання теореми Чебишева є ширшим, але емпіричне правило забезпечує більш точні результати для нормального розподілу.

Клацніть тут, щоб дізнатися, що таке емпіричне правило:

➤ Див.: загальне правило

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше