Як застосувати теорему чебишева в excel

Теорема Чебишева стверджує, що для будь-якого числа k, більшого за 1, принаймні 1 – 1/k ² значень даних у будь-якому навченому розподілі лежить у межах k стандартних відхилень від середнього.

Наприклад, для будь-якого формованого розподілу принаймні 1 – 1/3 ² = 88,89% значень у розподілі потраплятиме в межах 3 стандартних відхилень від середнього.

Цей посібник демонструє кілька прикладів застосування теореми Чебишева в Excel.

Приклад 1. Використовуйте теорему Чебишева, щоб визначити, який відсоток значень буде від 30 до 70 для набору даних із середнім значенням 50 і стандартним відхиленням 10.

Спочатку визначте значення k. Ми можемо зробити це, визначивши, скільки стандартних відхилень становить від 30 до 70 від середнього:

(30 – середнє) / стандартне відхилення = (30 – 50) / 10 = -20 / 10 = -2

(70 – середнє) / стандартне відхилення = (70 – 50) / 10 = 20 / 10 = 2

Значення 30 і 70 – це 2 стандартних відхилення нижче і вище середнього відповідно. Отже, k = 2 .

Потім ми можемо використати наступну формулу в Excel, щоб знайти мінімальний відсоток значень, які знаходяться в межах 2 стандартних відхилень від середнього для цього набору даних:

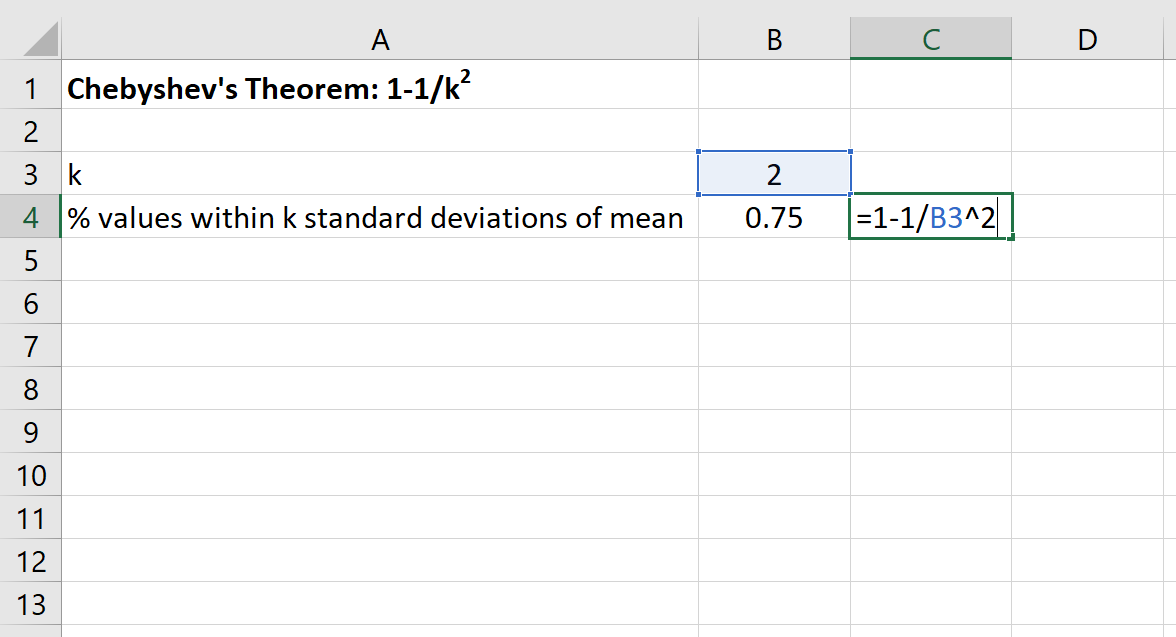
Відсоток значень від 30 до 70 для цього набору даних буде щонайменше 75% .

Приклад 2. Використовуйте теорему Чебишева, щоб визначити, який відсоток значень буде від 20 до 50 для набору даних із середнім значенням 35 і стандартним відхиленням 5.

Спочатку визначте значення k. Ми можемо зробити це, визначивши, скільки стандартних відхилень становить від 20 до 50 від середнього:

(20 – середнє) / стандартне відхилення = (20 – 35) / 5 = -15 / 5 = -3

(50 – середнє) / стандартне відхилення = (50 – 35) / 5 = 15 / 5 = 3

Значення 20 і 50 є 3 стандартними відхиленнями нижче і вище середнього відповідно. Отже, k = 3 .

Потім ми можемо використати наступну формулу в Excel, щоб знайти мінімальний відсоток значень, які знаходяться в межах 3 стандартних відхилень від середнього для цього набору даних:

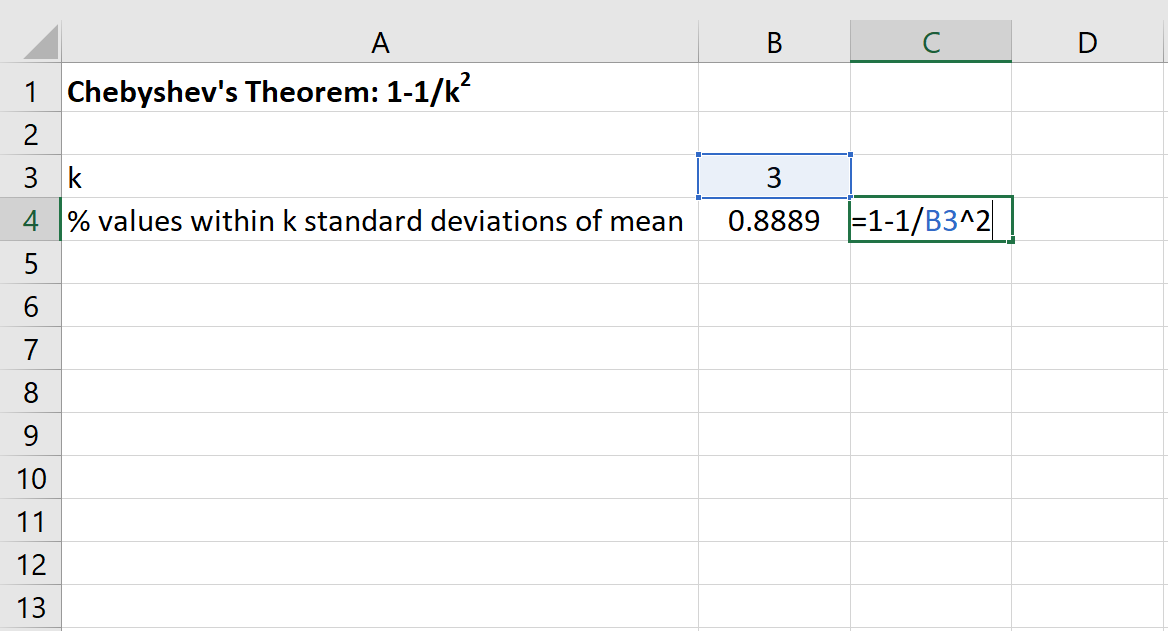
Відсоток значень від 20 до 50 для цього набору даних буде принаймні 88,89% .

Приклад 3. Використовуйте теорему Чебишева, щоб визначити, який відсоток значень буде від 80 до 120 для набору даних із середнім значенням 100 і стандартним відхиленням 5.

Спочатку визначте значення k. Ми можемо зробити це, визначивши, скільки стандартних відхилень становить від 80 до 120 від середнього:

(80 – середнє) / стандартне відхилення = (80 – 100) / 5 = -20 / 5 = -4

(120 – середнє) / стандартне відхилення = (120 – 100) / 5 = 20 / 5 = 4

Значення 80 і 120 є 4 стандартними відхиленнями нижче і вище середнього відповідно. Отже, k = 4 .

Потім ми можемо використати таку формулу в Excel, щоб знайти мінімальний відсоток значень, які потрапляють у межах 4 стандартних відхилень від середнього для цього набору даних:

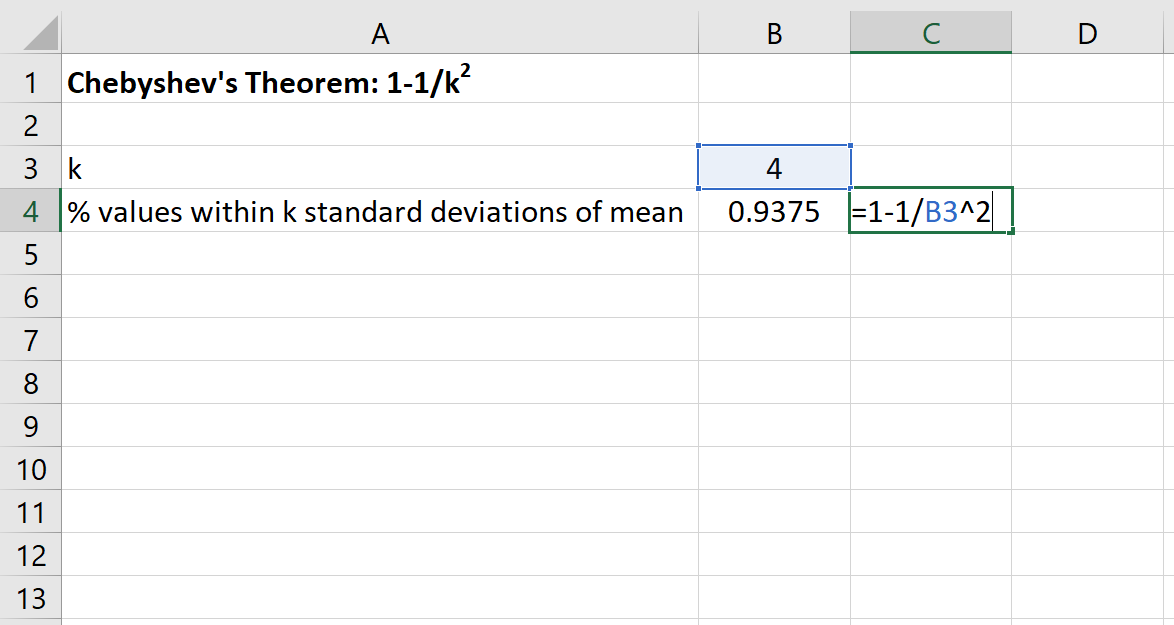
Відсоток значень від 80 до 120 для цього набору даних буде щонайменше 93,75% .