Як виконати одновибірковий t-тест у sas

Т-критерій для однієї вибірки використовується, щоб визначити, чи дорівнює середнє значення сукупності певному значенню.

У цьому підручнику пояснюється, як виконати одновибірковий t-тест у SAS.

Приклад: зразок t-критерію в SAS

Припустимо, ботанік хоче знати, чи дорівнює середня висота певного виду рослин 15 дюймам. Вона бере випадкову вибірку з 12 рослин і записує кожну їх висоту в дюймах.

Висота: 14, 14, 16, 13, 12, 17, 15, 14, 15, 13, 15, 14

Виконайте наступні кроки, щоб виконати t-тест для одного зразка, щоб визначити, чи справді середня висота цього виду рослин становить 15 дюймів.

Крок 1: Створіть дані.

Спочатку ми використаємо наступний код для створення набору даних у SAS:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*print dataset*/
proc print data =my_data; 

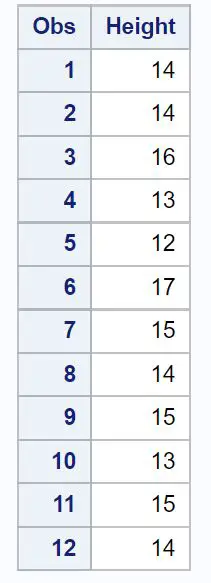
Крок 2: Виконайте t-критерій для однієї вибірки.

Далі ми використаємо proc ttest для виконання t-тесту на прикладі:

 /*perform one sample t-test*/
proc ttest data =my_data sides = 2 alpha = 0.05 h0 = 15 ;
    varHeight ;
run ;

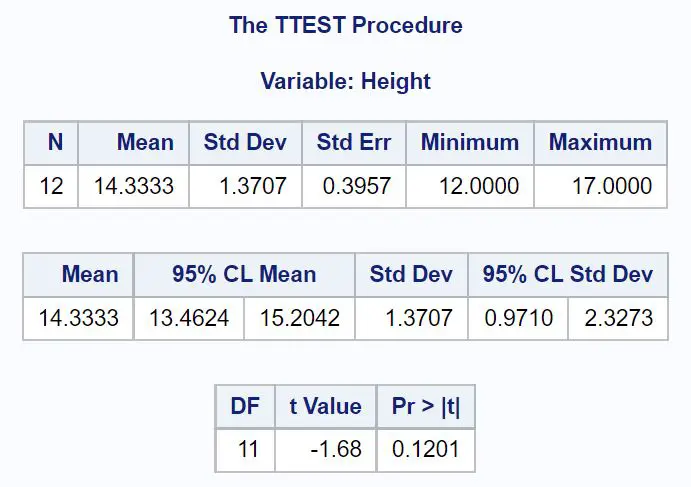
Перша таблиця відображає описову статистику для нашої вибірки, зокрема:

• N (загальна кількість спостережень): 12
• Середнє (середнє за вибіркою): 14,3333
• Стандартне відхилення (вибіркове стандартне відхилення): 1,3707
• Стандартна помилка (стандартна помилка, розрахована як s/ √n ): 0,3957
• Мінімум (мінімальне значення): 12
• Максимум (максимальне значення) 17

Друга таблиця відображає 95% довірчий інтервал для справжнього середнього значення сукупності:

• 95% ДІ для μ: [13,4624, 15,2042]

Третя таблиця відображає статистику t-критерію та відповідне значення p:

• t-критерій статистики: -1,68
• p-значення: 0,1201

Примітка . Тестову статистику було розраховано таким чином:

• t тестова статистика = ( x – μ) / (s/ √n )
• t-критерій статистики = (14,3333-15) / (1,3707/√ 12 )
• t-критерій статистики = -1,68

Нагадаємо, що одновибірковий t-критерій використовує такі нульові та альтернативні гіпотези:

• H ₀ : μ = 15 дюймів
• H _A : μ ≠ 15 дюймів

Оскільки p-значення ( 0,1201 ) не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Це означає, що у нас недостатньо доказів, щоб стверджувати, що середня висота деяких видів рослин відрізняється від 15 дюймів.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші поширені статистичні тести в SAS:

Як виконати тест Вілкоксона зі знаком рангу в SAS
Як виконати односторонній дисперсійний аналіз у SAS