Як виконати тест даннетта в r

Post hoc тест — це тип тесту, який виконується після дисперсійного аналізу , щоб визначити, які групові середні значення статистично суттєво відрізняються одне від одного.

Якщо одна з досліджуваних груп вважається контрольною , тоді ми повинні використовувати тест Даннетта як додатковий тест.

Цей підручник пояснює, як виконати тест Даннетта в R.

Приклад: тест Даннета в R

Припустімо, що вчитель хоче знати, чи можуть дві нові методи навчання покращити результати тестів її учнів. Щоб перевірити це, вона випадковим чином ділить свій клас із 30 учнів на такі три групи:

• Контрольна група: 10 студентів
• Новий технічний кабінет 1: 10 студентів
• Новий технічний кабінет 2: 10 студентів

Після тижня використання призначеної методики навчання кожен студент складає той самий іспит.

Ми можемо використати наступні кроки в R, щоб створити набір даних, візуалізувати групові середні, виконати односторонній дисперсійний аналіз і, нарешті, виконати тест Даннета, щоб визначити, яка нова методика дослідження (якщо така є) дає інші результати порівняно з контрольною групою .

Крок 1: Створіть набір даних.

Наступний код показує, як створити набір даних, що містить результати іспитів усіх 30 студентів:

 #create data frame
data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 control 76
2 controls 77
3 controls 77
4 controls 81
5 controls 82
6 controls 82

Крок 2: Перегляньте результати іспиту для кожної групи.

У наведеному нижче коді показано, як створити коробкові діаграми для візуалізації розподілу результатів іспитів для кожної групи:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

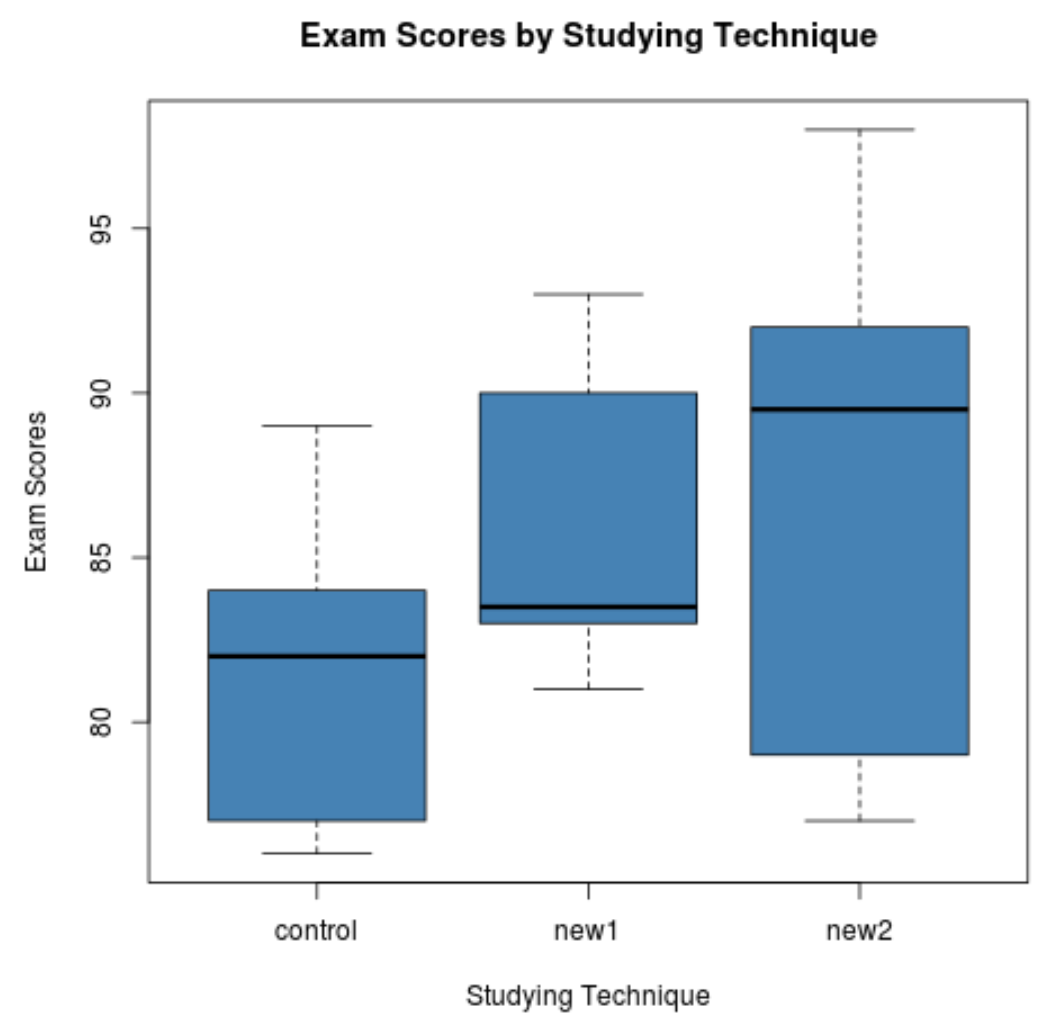
Лише з коробкових графіків ми бачимо, що розподіл іспитових балів дуже відрізняється для кожної методики навчання. Потім ми виконаємо односторонній дисперсійний аналіз, щоб визначити, чи є ці відмінності статистично значущими.

Пов’язане: Як побудувати кілька діаграм в одній діаграмі в R

Крок 3: Виконайте односторонній дисперсійний аналіз.

У наведеному нижче коді показано, як виконати односторонній дисперсійний аналіз, щоб перевірити різницю між середніми оцінками іспиту в кожній групі:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Оскільки загальне значення p ( 0,0476 ) менше 0,05, це означає, що кожна група не має однакового середнього балу за іспит. Далі ми виконаємо тест Даннетта, щоб визначити, яка методика навчання дає середні результати іспитів, які відрізняються від результатів контрольної групи.

Крок 4: Виконайте тест Даннета.

Щоб виконати тест Dunnett у R, ми можемо використати функцію DunnettTest() із бібліотеки DescTools , яка використовує такий синтаксис:

Критерій Даннета (x, g)

золото:

• x: числовий вектор значень даних (наприклад, результати іспиту)
• g: вектор, що вказує назви груп (наприклад, метод дослідження)

Наступний код показує, як використовувати цю функцію для нашого прикладу:

 #load DescTools library
library(DescTools)

#perform Dunnett's Test
DunnettTest(x=data$score, g=data$technique)

  Dunnett's test for comparing several treatments with a control:  
    95% family-wise confidence level

$control
             diff lwr.ci upr.ci pval    
new1-control 4.2 -1.6071876 10.00719 0.1787    
new2-control 6.4 0.5928124 12.20719 0.0296 *  

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1

Спосіб інтерпретації результату такий:

• Середня різниця в іспитових балах між новою методикою дослідження 1 і контрольною групою становить 4,2. Відповідне значення p становить 0,1787 .
• Середня різниця в іспитових балах між новою методикою навчання 2 і контрольною групою становить 6,4. Відповідне значення p становить 0,0296 .

Грунтуючись на результатах, ми можемо побачити, що вивчення Техніки 2 є єдиною технікою, яка дає середні оцінки іспиту, які значно (p = 0,0296) відрізняються від показників контрольної групи.

Додаткові ресурси

Вступ до одностороннього дисперсійного аналізу
Як виконати односторонній дисперсійний аналіз у R
Як виконати тест Тьюкі в R