4 приклади використання тестів хі-квадрат у реальному житті
У статистиці існує два різних типи тестів хі-квадрат:
1. Критерій відповідності хі-квадрат – використовується для визначення того, чи відповідає категоріальна змінна гіпотетичному розподілу.
2. Тест незалежності хі-квадрат – використовується для визначення того, чи існує значний зв’язок між двома категоріальними змінними.
У цій статті ми наведемо кілька прикладів того, як кожен із цих типів тестів хі-квадрат використовується в реальних ситуаціях.
Приклад 1: Тест відповідності хі-квадрат
Припустімо, що власник магазину стверджує, що кожен день тижня до його магазину приходить однакова кількість покупців.
Щоб перевірити цю гіпотезу, він записує кількість клієнтів, які прийшли в магазин за певний тиждень, і знаходить наступне:
- Понеділок: 50 клієнтів
- Вівторок: 60 клієнтів
- Середа: 40 клієнтів
- Четвер: 47 клієнтів
- П’ятниця: 53 клієнтів
Він може використовувати тест відповідності хі-квадрат, щоб визначити, чи відповідає розподіл клієнтів, які приходять щодня, його гіпотезі розподілу.
Використовуючи калькулятор тесту відповідності хі-квадрат , він може побачити, що p-значення тесту становить 0,359 .
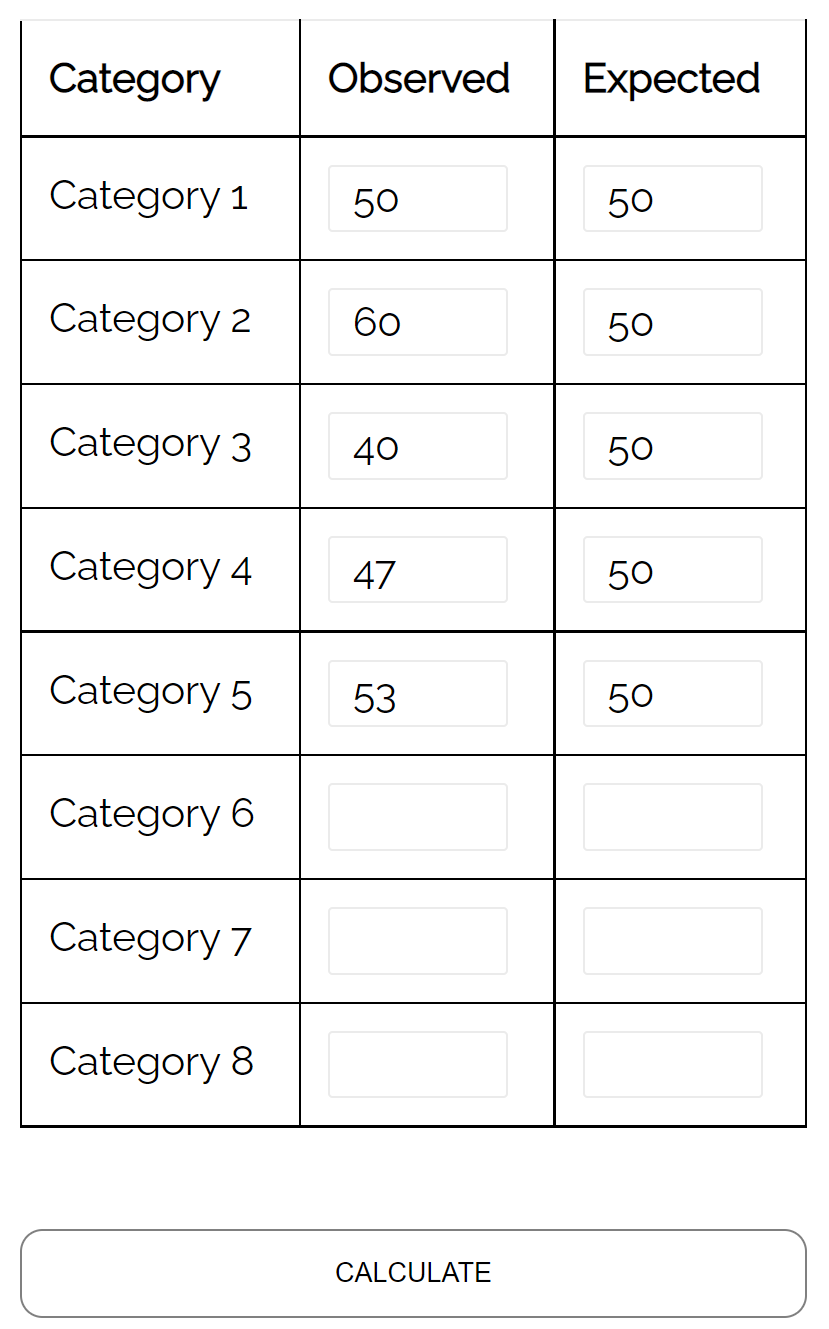

Оскільки це p-значення не менше 0,05, немає достатніх доказів, щоб стверджувати, що справжній розподіл клієнтів відрізняється від того, який заявляє власник магазину.
Приклад 2: Тест відповідності хі-квадрат
Припустімо, біолог стверджує, що рівна кількість чотирьох різних видів оленів щотижня потрапляє в певну лісисту зону лісу.
Щоб перевірити цю гіпотезу, вона записує кількість кожного виду оленів, які потрапляють у лісисту місцевість протягом тижня:
- Вид №1: 22
- Вид №2: 20
- Види №3: 23
- Види №4: 35
Вона може використати тест відповідності хі-квадрат, щоб визначити, чи відповідає розподіл видів оленів, які щотижня потрапляють у лісову зону лісу, їх гіпотетичному розподілу.
Використовуючи калькулятор тесту відповідності хі-квадрат , вона може побачити, що p-значення для тесту становить 0,137 .
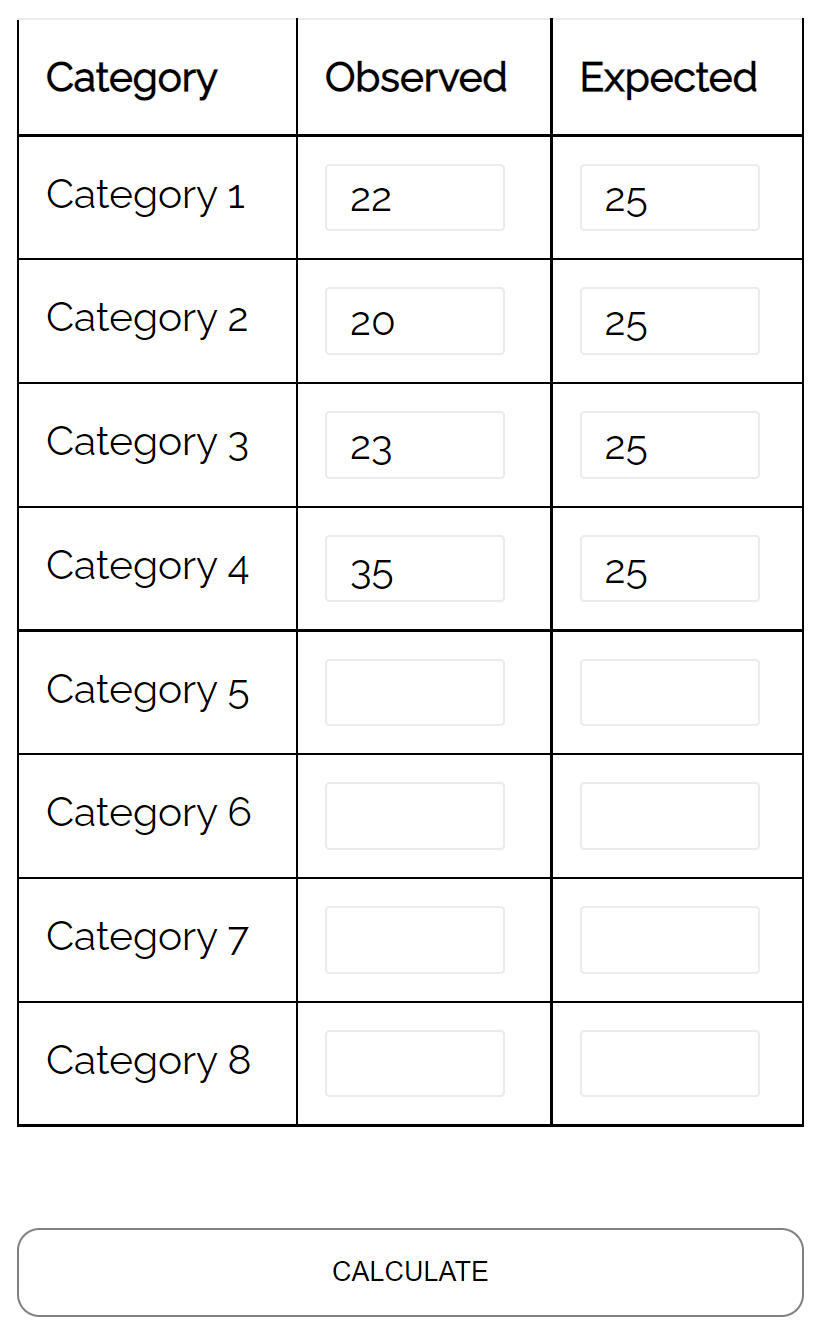
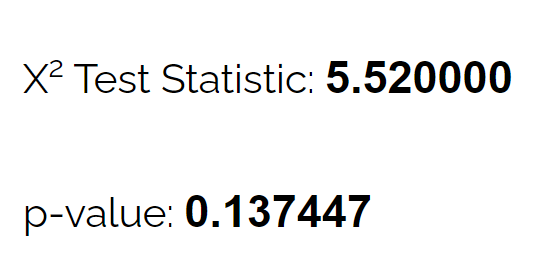
Оскільки це значення p не менше 0,05, немає достатніх доказів, щоб стверджувати, що справжній розподіл оленів відрізняється від того, що стверджує біолог.
Приклад 3: тест на незалежність хі-квадрат
Припустімо, що політик у певному місті хоче знати, чи пов’язана стать із уподобаннями політичної партії.
Він вирішує взяти просту випадкову вибірку з 500 виборців і запитати їх про їхні переваги щодо політичної партії. У наступній таблиці представлені результати опитування:
| республіканець | демократ | Незалежний | Всього | |
| Чоловік | 120 | 90 | 40 | 250 |
| Жінка | 110 | 95 | 45 | 250 |
| Всього | 230 | 185 | 85 | 500 |
Він може використовувати тест хі-квадрат незалежності , щоб визначити, чи існує статистично значущий зв’язок між двома змінними.
Використовуючи калькулятор тесту незалежності хі-квадрат , він може побачити, що p-значення тесту становить 0,649 .
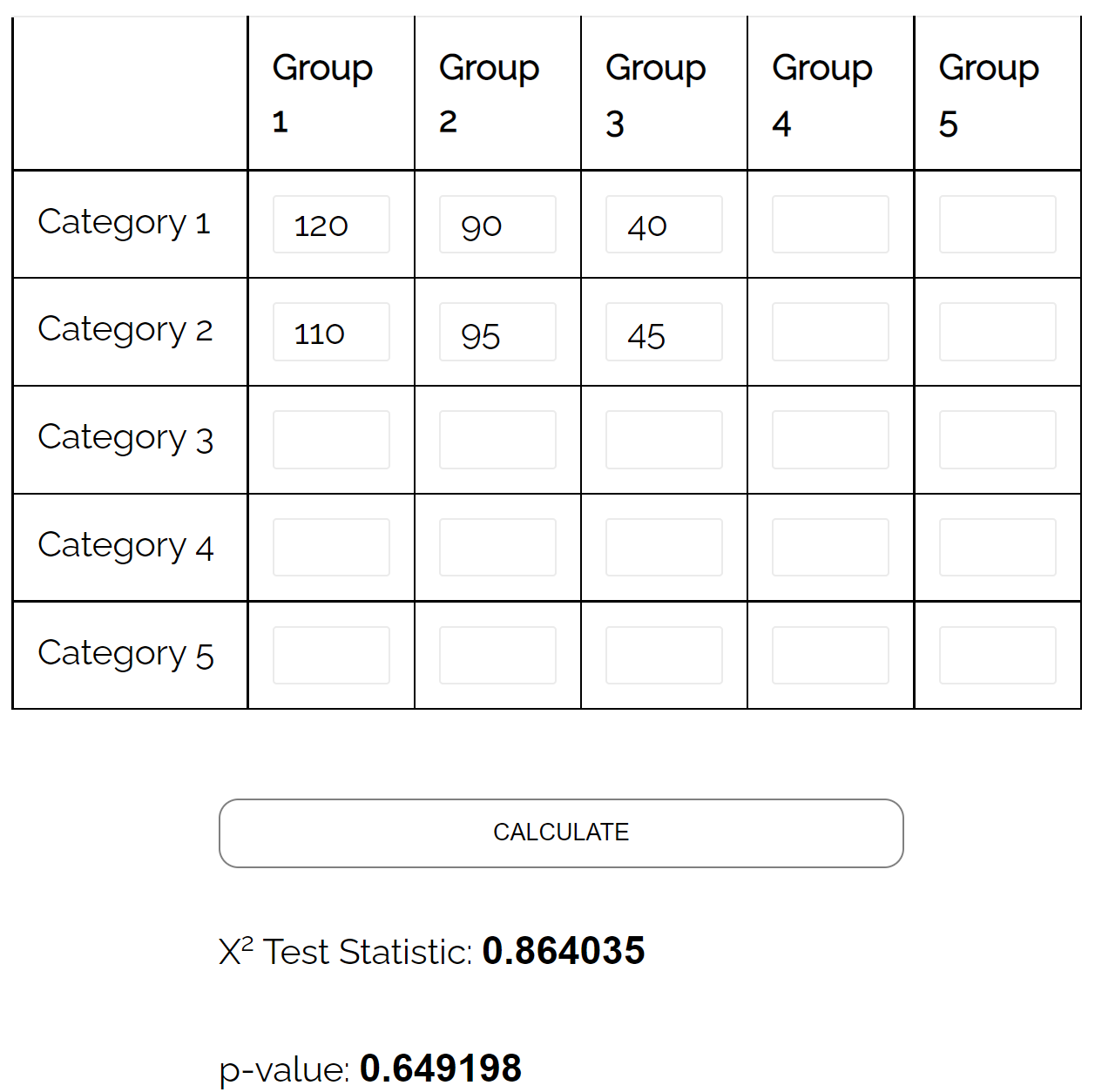
Оскільки p-значення не менше 0,05, немає достатніх доказів, щоб стверджувати, що існує зв’язок між статтю та перевагами політичної партії.
Приклад 4: тест на незалежність хі-квадрат
Припустімо, дослідник хоче знати, чи пов’язаний сімейний стан з рівнем освіти.
Він вирішує взяти просту випадкову вибірку з 300 осіб і отримує такі результати:
| Вища школа | Холостяки | Магістр або вище | Всього | |
| Одружений | 20 | 100 | 35 | 155 |
| Бакалавр | 50 | 80 | 15 | 145 |
| Всього | 70 | 180 | 50 | 300 |
Він може використовувати тест хі-квадрат незалежності , щоб визначити, чи існує статистично значущий зв’язок між двома змінними.
Використовуючи калькулятор тесту незалежності хі-квадрат , він може побачити, що p-значення тесту становить 0,000011 .
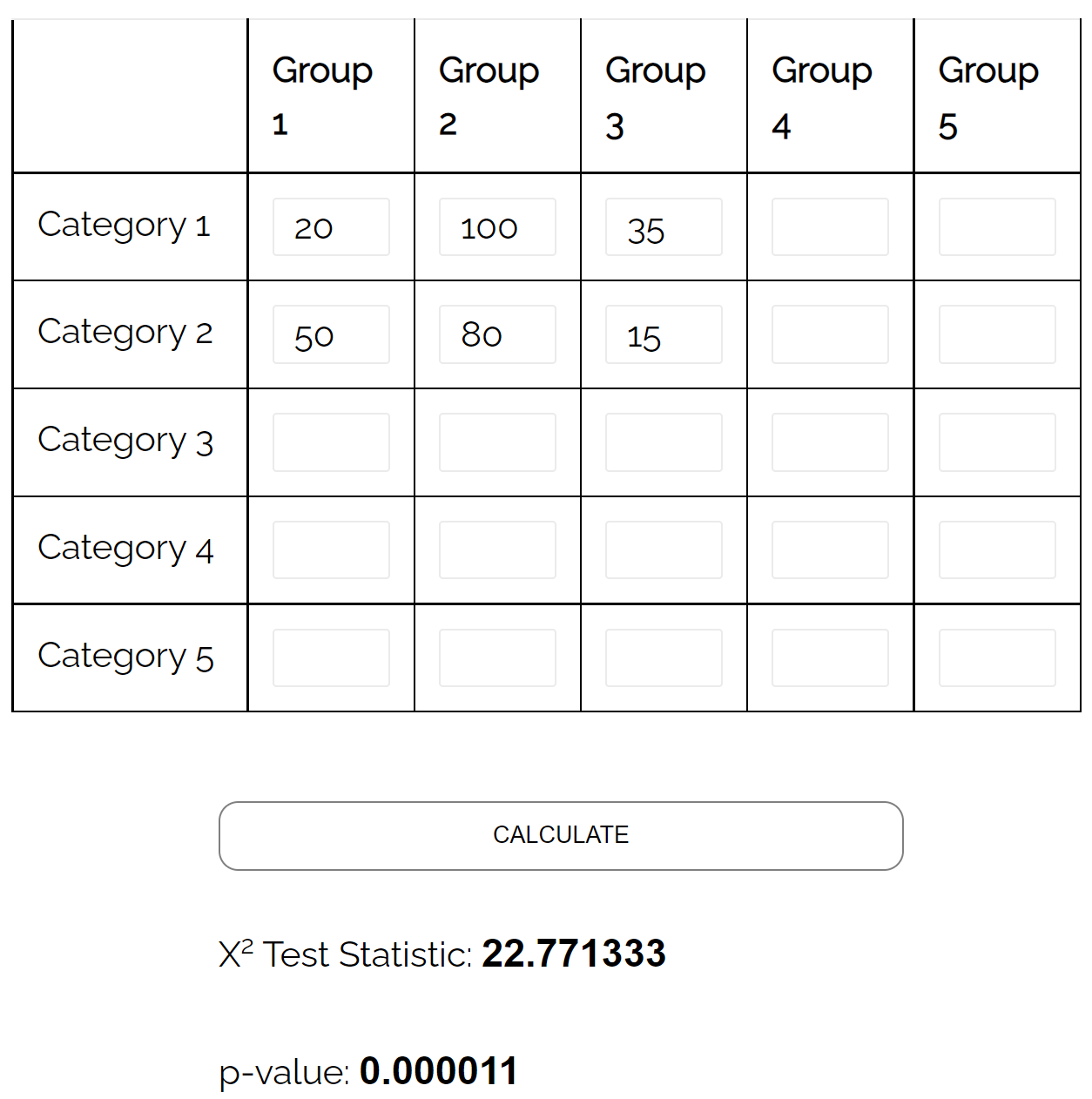
Оскільки p-значення менше 0,05, є достатньо доказів, щоб стверджувати, що існує зв’язок між сімейним станом і рівнем освіти.
Додаткові ресурси
Наступні навчальні посібники містять введення в різні типи тестів хі-квадрат:
У наступних посібниках пояснюється різниця між тестами хі-квадрат та іншими статистичними тестами: