Як виконати тест відповідності хі-квадрат у spss

Тест відповідності хі-квадрат використовується для визначення того, чи відповідає категоріальна змінна гіпотетичному розподілу.

У цьому посібнику пояснюється, як виконати тест відповідності хі-квадрат у SPSS.

Приклад: Тест хі-квадрат відповідності в SPSS

Власник магазину каже, що кожен день тижня до його магазину приходить однакова кількість покупців. Щоб перевірити цю гіпотезу, дослідник записує кількість покупців, які прийшли в магазин за певний тиждень, і знаходить наступне:

• Понеділок: 50 клієнтів
• Вівторок: 60 клієнтів
• Середа: 40 клієнтів
• Четвер: 47 клієнтів
• П’ятниця: 53 клієнтів

Виконайте наступні кроки, щоб виконати тест відповідності хі-квадрат у SPSS, щоб визначити, чи дані відповідають твердженням власника магазину.

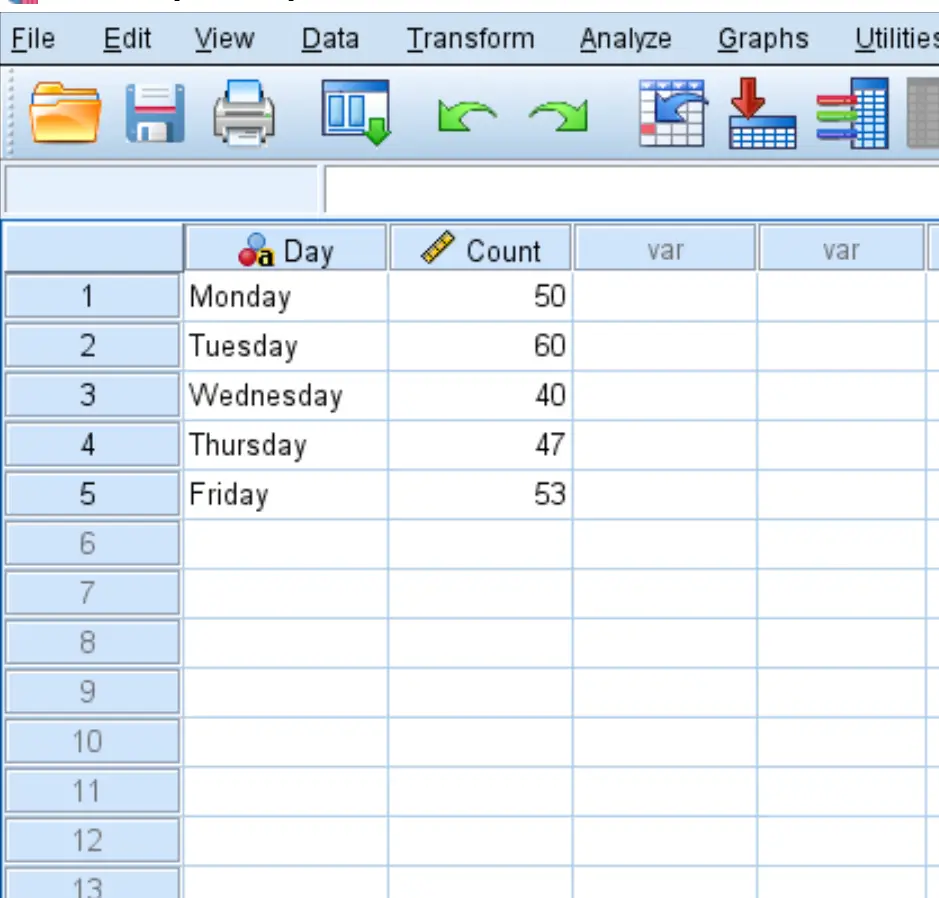
Крок 1: Введіть дані.

Спочатку введіть дані в SPSS у такому форматі:

Крок 2. Використовуйте зважені ящики.

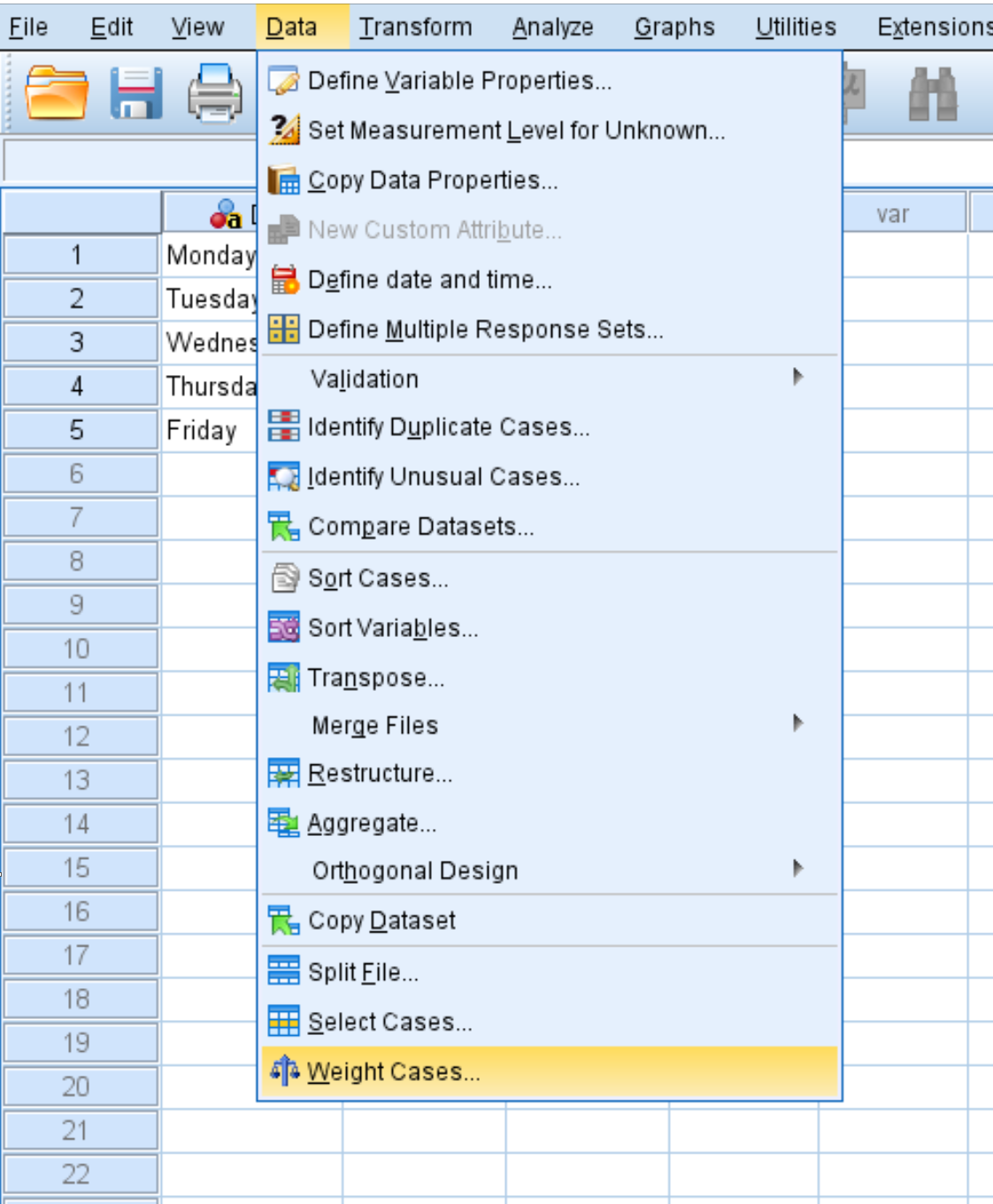
Щоб тест працював правильно, нам потрібно повідомити SPSS, що змінна «День» повинна бути зважена змінною «Число».

Клацніть вкладку Дані , а потім клацніть Випадки ваги :

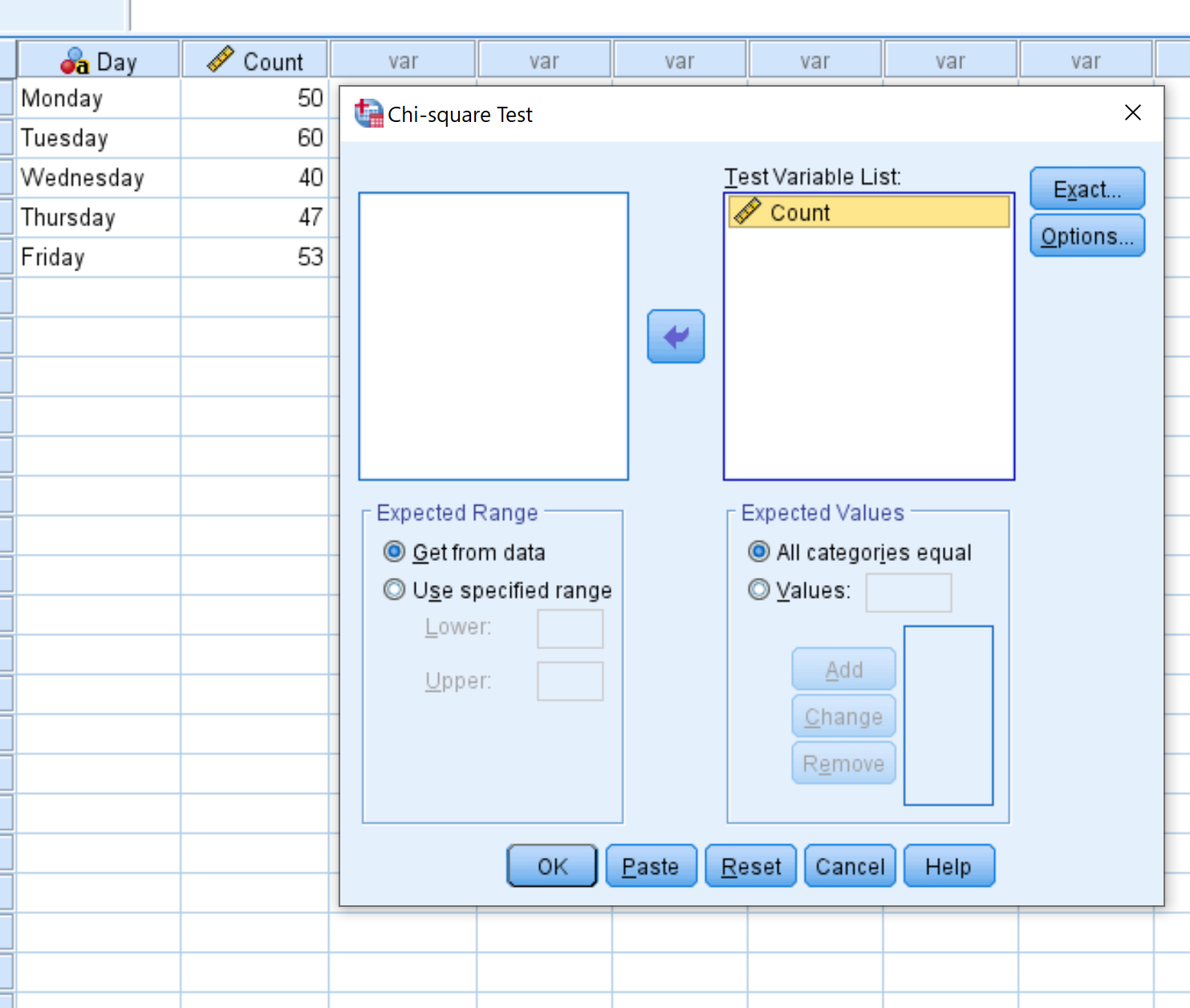
У новому вікні, що з’явиться, перетягніть змінну Count у область під назвою «Список тестових змінних». Потім натисніть OK .

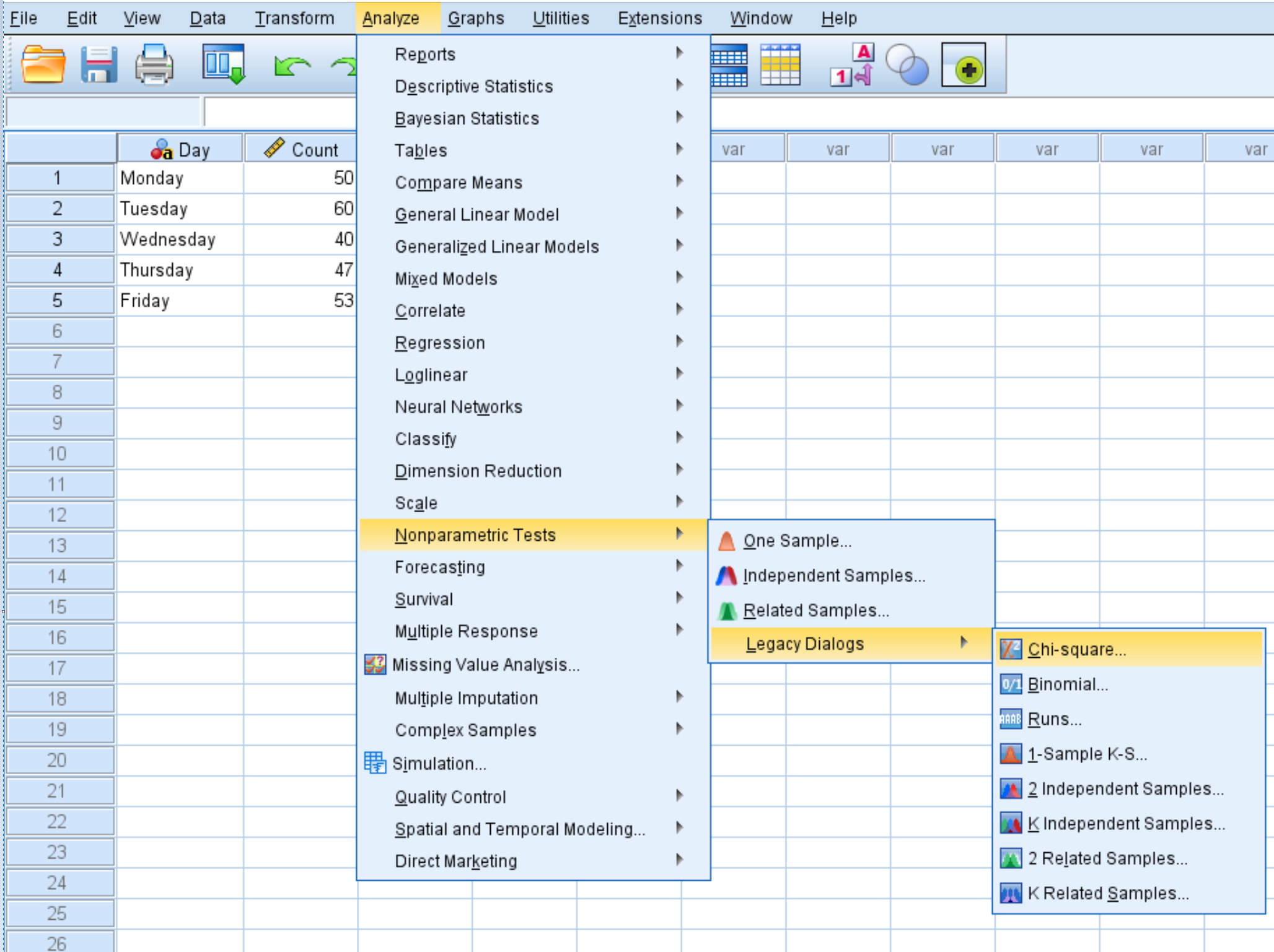
Крок 3. Виконайте тест на відповідність хі-квадрат.

Клацніть вкладку «Аналіз» , потім «Непараметричні тести» , потім «Застарілі діалоги» , потім «Хі-квадрат» :

У новому вікні, що з’явиться, перетягніть змінну Count у область під назвою «Список тестових змінних».

Залиште позначку поруч із Усі категорії рівними, оскільки кожна з наших категорій (тобто днів тижня) має однакову очікувану кількість відвідувачів щодня. Потім натисніть OK .

Крок 4: Інтерпретуйте результати .

Після натискання кнопки OK з’являться результати тесту відповідності хі-квадрат:

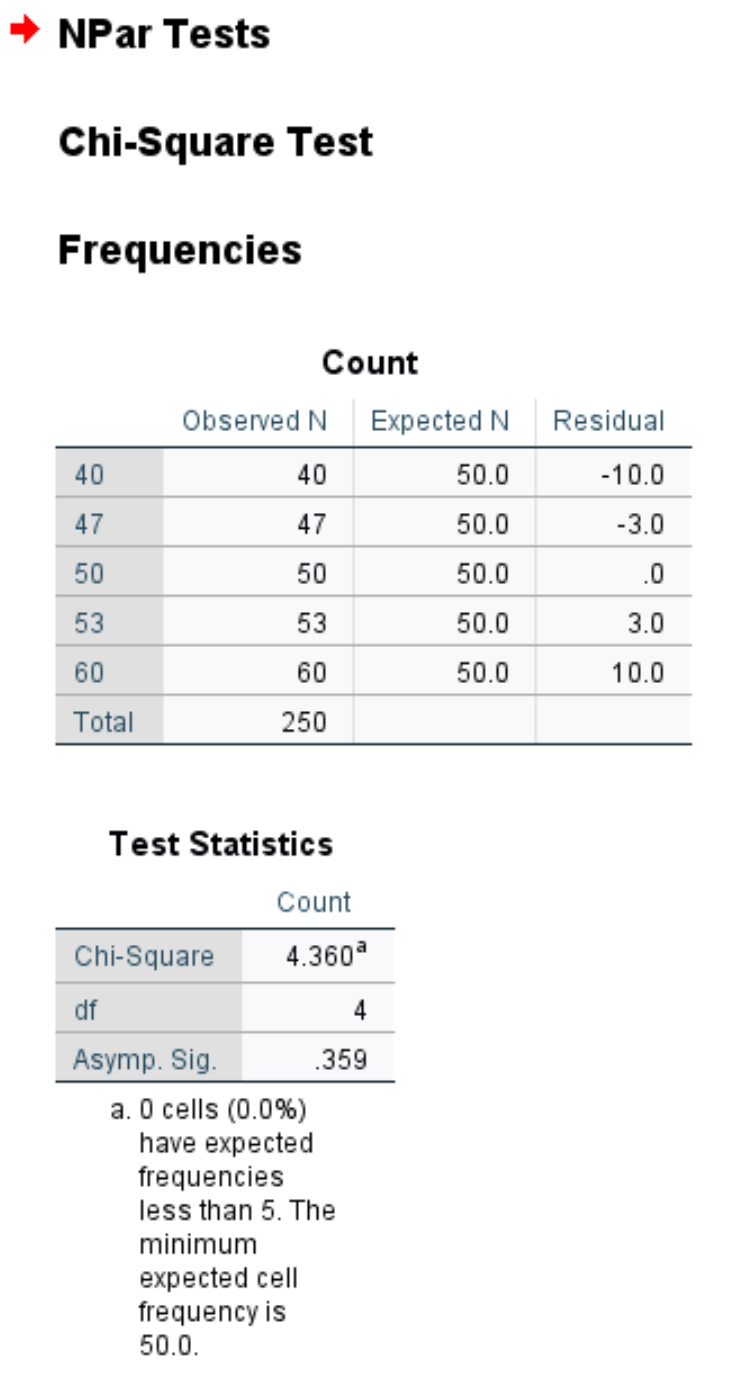
Перша таблиця показує спостережувану та очікувану кількість клієнтів кожного дня тижня, а також залишок (тобто різницю) між спостережуваною та очікуваною.

У другій таблиці відображаються такі числа:

Хі-квадрат: статистика хі-квадрат, яка становить 4,36.

df: Ступені свободи, обчислені як #categories-1 = 5-1 = 4.

Асимп. Sig: P-значення, яке відповідає значенню хі-квадрат 4,36 з 4 ступенями свободи, що становить 0,359. Це значення також можна знайти за допомогою калькулятора співвідношення хі-квадрат до значення P.

Оскільки p-значення (0,359) не менше 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що справжній розподіл клієнтів відрізняється від того, про який повідомляє власник магазину.