Введення

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що означає характеризувати розподіл у статистиці. Таким чином, ви знайдете визначення типізації, приклад типізації змінної і, крім того, ви зможете попрактикуватися з вправою, розв’язаною крок за кроком.

Що таке набір тексту?

У статистиці нормалізація — це процес, у якому лінійне перетворення застосовується до розподілу таким чином, що його середнє та стандартне відхилення дорівнюють нулю та одиниці відповідно.

Точніше, введення включає віднімання середнього значення від випадкової змінної, а потім його ділення на стандартне відхилення.

Типізацію також можна назвати нормалізацією або стандартизацією.

Формула введення

Щоб класифікувати змінну, ви повинні відняти її середнє значення, а потім розділити його на стандартне відхилення. Тому формула для введення змінної виглядає наступним чином:

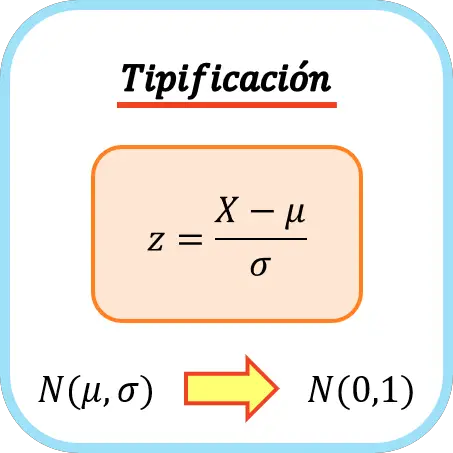
золото

$\mu$

є середнім значенням змінної

$X$

$\sigma$

його стандартне відхилення (або стандартне відхилення).

Таким чином, запис фактично є зміною змінної, оскільки до змінної застосовано лінійне перетворення.

Приклад запису

Розглядаючи визначення типізації та її формулу, нижче наведено конкретний приклад, щоб повністю зрозуміти цю концепцію.

Безперервна випадкова змінна відповідає нормальному розподілу із середнім значенням 45 і стандартним відхиленням 10. Яка ймовірність отримати значення, менше або дорівнює 60?

$N(45,10)$

Щоб знайти ймовірність нормального розподілу, нам потрібно використовувати його таблицю характеристик, але для цього нам потрібно спочатку виконати процес введення. Тому ми віднімаємо середнє значення та ділимо на стандартне відхилення до значення ймовірності:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Після стандартизації ми переходимо до таблиці ймовірностей нормального розподілу, щоб побачити, якій ймовірності відповідає значення 1,5:

Як видно з таблиці типізації нормального розподілу, значення, обчислене на попередньому кроці, відповідає такій ймовірності:

$\displaystyle P(Z\leq 1,5)=0,9332$

Таким чином, ймовірність отримати значення, рівне або менше 60, становить 93,32%.

Розв’язана вправа з друкування

Обчисліть такі ймовірності нормального розподілу, середнє та стандартне відхилення якого дорівнюють 120 і 50 відповідно.

$N(120,50)$

Ймовірність отримати значення, менше або дорівнює 208.
Імовірність отримання значення більше 137.

Подивіться рішення

В обох розділах задачі нам потрібно ввести нормальний розподіл, щоб обчислити ймовірності.

Ми починаємо з обчислення ймовірності введення значення, меншого або еквівалентного 208:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

А тепер подивимося в таблиці вище, якій ймовірності відповідає значення 1,76:

$\displaystyle P(Z\leq 1,76)=0,9608$

По-друге, ми розрахуємо ймовірність отримати значення більше 137. Таким же чином ми починаємо з введення змінної:

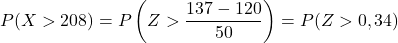$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ Однак додана таблиця має лише найнижчу кумулятивну ймовірність, тому для використання таблиці ми повинні спочатку перетворити ймовірність:

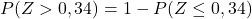$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ І, нарешті, зазначимо з доданої таблиці ймовірність, що відповідає розрахованому значенню Z:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

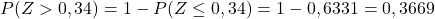
Який сенс друкувати?

Щоб завершити розуміння значення типізації, ми побачимо, для чого вона використовується та коли змінну потрібно вводити.

В основному стандартизація використовується для порівняння значень розподілів з різними середніми значеннями та дисперсіями. Подібним чином стандартизація також використовується для розрахунку ймовірності.

Стандартизуючи два значення розподілу з різними характеристиками, ми можемо побачити, яке значення більше або менше відносно всього розподілу. Іншими словами, застосовуючи процес типізації, ми можемо побачити, яке значення є найближчим або найдальшим від середнього значення його розподілу.

Крім того, як пояснювалося вище, типізація також дозволяє обчислювати ймовірності, оскільки, як правило, таблиці ймовірностей базуються на типізованому розподілі.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше