Умовна ймовірність (або умовна ймовірність)

за Редакція 6 Серпня, 2023 Ймовірність 0 коментарів

Тут ви дізнаєтесь, що таке умовна ймовірність (або умовна ймовірність). Ми пояснюємо, як обчислюється умовна ймовірність на прикладі та властивості цього типу ймовірності. Крім того, ви зможете попрактикуватися з покроковими розв’язуваннями вправ на умовну ймовірність.

Що таке умовна ймовірність?

Умовна ймовірність , також звана умовною ймовірністю , є статистичним показником, який вказує ймовірність того, що подія A відбудеться, якщо відбудеться інша подія B. Тобто умовна ймовірність P(A|B) відноситься до ймовірності події A після того, як подія B вже відбулася.

Умовна ймовірність записується вертикальною рискою між двома подіями: P(A|B) і читається: «умовна ймовірність події A при даній події B».

Зауважте, що значення умовної ймовірності є числом від 0 до 1. Чим вища умовна ймовірність, тим більша ймовірність того, що подія A відбудеться разом із подією B, але чим нижча умовна ймовірність, тим менша ймовірність події A станеться, коли відбудеться подія B.

Формула умовної ймовірності

Умовна ймовірність події A даної події B дорівнює ймовірності перетину подій A і B, поділеній на ймовірність події B.

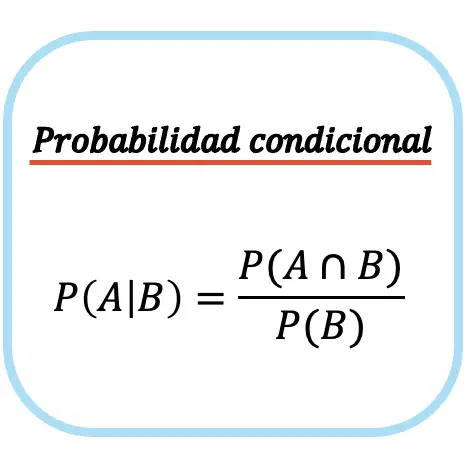
Зауважте, що формулу умовної ймовірності (або умовної ймовірності) можна використовувати, лише якщо ймовірність настання безумовної події відмінна від нуля, тобто P(B)≠0. Або іншими словами, чи можлива подія B.

Умовну ймовірність також можна обчислити за її зворотною ознакою, тобто якщо відоме P(B|A), можна визначити P(A|B). Але для цього ви повинні застосувати теорему Байєса, ви можете побачити, з чого складається ця теорема:

➤ Дивіться: Що таке теорема Байєса?

Приклад умовної ймовірності

Коли ми побачимо, що таке визначення та формула умовної ймовірності, ми крок за кроком розв’яжемо приклад цього типу ймовірності, щоб повністю зрозуміти її значення.

Після складання іспиту в класі з 30 студентів було зібрано дані, щоб дізнатися, скільки студентів навчалося і скільки здали. Результати представлені в наступній таблиці непередбачених обставин. На основі зібраних даних обчисліть умовну ймовірність здачі іспиту, якщо ви вже вчилися.

Щоб отримати умовну ймовірність, ми повинні застосувати формулу, яку ми бачили раніше:

$P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}$

Отже, нам спочатку потрібно знайти ймовірність того, що студент навчався, навчався і склав. Щоб знайти ймовірність того, що студент навчався, нам просто потрібно скористатися правилом Лапласа, тобто кількість студентів, які навчалися, розділити на загальну кількість спостережень:

$P(\text{estudiado})=\cfrac{23}{30}=0,77$

А ймовірність того, що студент навчався і здав одночасно, ми можемо дізнатися з таблиці непередбачуваності, поділивши кількість студентів, які вчилися і здали, на загальну суму:

$P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63$

Таким чином, ймовірність того, що студент складе іспит, якщо він навчався, становить:

$\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}$

Умовна ймовірність залежних і незалежних подій

У цьому розділі ми побачимо, який зв’язок між умовною ймовірністю та залежними та незалежними подіями (або залежними та незалежними подіями). Тому що, хоча це різні поняття, ці два типи подій пов’язані з умовною ймовірністю.

Дві події (або події) є незалежними, якщо ймовірність їх появи не залежить одна від одної. У такому випадку перетин між двома подіями еквівалентний добутку ймовірності кожної події окремо. І, отже, формула умовної ймовірності спрощена:

$P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)$

Коротше кажучи, якщо події A і B незалежні, умовна ймовірність події A даної події B точно дорівнює ймовірності події A.

З іншого боку, коли дві події є залежними, це означає, що ймовірність однієї події залежить від ймовірності іншої події. Отже, коли дві події A і B є залежними, умовна ймовірність події A даної події B відрізняється від ймовірності появи події A.

$P(A|B)\neq P(A)$

Розв’язані вправи на умовну ймовірність

Вправа 1

Ми знаємо, що в мішку, наповненому кульками, половина помаранчева, а інша зелена. Крім того, третина всіх куль помаранчеві і водночас позначені знаком. Яка ймовірність того, що коли ви витягнете помаранчеву кульку, вона отримає сигнал?

Подивіться рішення

Щоб розв’язати вправу, ми повинні застосувати умовну формулу ймовірності, яка є:

$P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}$

Постановка задачі говорить нам, що половина мішка — апельсини. Тому теоретична ймовірність підібрати помаранчевий м’яч становить 50%.

$P(\text{naranja})=\cfrac{1}{2}=0,5$

З іншого боку, ми знаємо, що третина від загальної кількості – це помаранчеві кулі з сигналом, тому ймовірність отримати помаранчеву кулю з сигналом дорівнює:

$P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33$

Нарешті, ми підставляємо обчислені ймовірності у формулу умовної ймовірності, щоб знайти її значення:

$\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}$

Підсумовуючи, ймовірність витягнути кулю за сигналом, якщо вона помаранчева, становить 66%.

Вправа 2

Якщо у нас є шість синіх ручок і три чорні ручки в коробці, обчисліть ймовірність намалювати одну синю ручку та ймовірність намалювати дві сині ручки поспіль.

Подивіться рішення

Щоб визначити ймовірність одного разу взяти в руки синю ручку, просто скористайтеся законом Лапласа:

$P(\text{azul})=\cfrac{6}{6+3}=0,67$

У задачі також вимагається знати ймовірність взяти дві сині ручки поспіль, тобто умовну ймовірність взяти синю ручку, якщо ми вже взяли синю ручку раніше.

Якщо ми намалюємо синю ручку, у нас менш сприятливий випадок, але в загальній кількості на одну ручку менше. Отже, умовна ймовірність:

$P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63$

Вправа 3

Яка умовна ймовірність кинути кубик до числа 4, враховуючи, що підкидання монети закінчується головами?

Подивіться рішення

Щоб розв’язати цю вправу, необхідно взяти до уваги теорію умовної ймовірності, оскільки події «отримання числа 4 киданням кубика» та «отримання голів киданням монети» є незалежними. Тому немає необхідності використовувати формулу умовної ймовірності, але виконується наступна рівність:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})$

Отже, щоб знайти умовну ймовірність, просто скористайтеся правилом Лапласа:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167$

Вправа 4

Було вивчено фінансовий рік 25 компаній у країні та те, як змінюються ціни їхніх акцій залежно від економічного результату року. Ви можете переглянути зібрані дані в наведеній нижче таблиці непередбачених ситуацій:

Наскільки ймовірно зростання курсу акцій компанії, якщо вона отримала прибуток за минулий рік?

Подивіться рішення

У вправі нас запитують про умовну ймовірність того, що запаси зростуть, якщо компанія досягла позитивного економічного результату. Отже, щоб обчислити цю ймовірність, ми повинні використовувати формулу умовної ймовірності:

$P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}$

Тому ми спочатку розраховуємо ймовірність того, що компанія отримає прибуток, а по-друге, ймовірність того, що компанія отримає економічний прибуток, підвищуючи свою ціну за акцію:

$P(\text{beneficio})=\cfrac{14}{25}=0,56$

$P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4$

А потім підставляємо знайдені значення в формулу і обчислюємо умовну ймовірність:

$\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}$

Властивості умовної ймовірності

Властивості умовної ймовірності, або умовної ймовірності, такі:

Сума умовної ймовірності події A даної події B плюс умовна ймовірність додаткової події A даної події B дорівнює одиниці.

$P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1$

Якщо подія A є підмножиною події B, A завжди відбуватиметься, коли B буде істинним. Таким чином, умовна ймовірність події A при даній події B у цих випадках дорівнює 1.

$B\subseteq A \ \longrightarrow \ P(A|B)=1$

Для двох різних подій завжди виконується наступна рівність щодо умовної ймовірності:

$P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке умовна ймовірність?

Формула умовної ймовірності

Приклад умовної ймовірності

Умовна ймовірність залежних і незалежних подій

Розв’язані вправи на умовну ймовірність

Вправа 1

Вправа 2

Вправа 3

Вправа 4

Властивості умовної ймовірності

Про автора

Редакція

Додати коментар