Функція ймовірності

за Редакція 5 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке функції ймовірності. Таким чином, ви знайдете значення функції ймовірності, її властивості та конкретний приклад обчислення функції ймовірності. Крім того, представлено відмінності між функцією ймовірності та іншими типами імовірнісних функцій.

Що таке функція ймовірності?

Функція ймовірності , також звана функцією маси ймовірності , — це математична функція, яка описує ймовірність того, що дискретна випадкова величина набуває певного значення.

Тобто функція ймовірності повертає ймовірність того, що дискретна змінна точно дорівнює значенню.

$f(x)=P[X=x]$

Наприклад, ймовірність кинути будь-яке число під час кидання кубика дорівнює 1/6 (у кубика є шість сторін), тому функція ймовірності, пов’язана з цим простором вибірки, дорівнюватиме 1/6 для n незалежно від значення.

Властивості функції ймовірності

Функції ймовірності мають такі властивості:

Імовірності не можуть бути від’ємними, тому функція ймовірностей дорівнює нулю або додатна для будь-якого значення x.

$f(x)\geq 0$

Аналогічно, максимальна ймовірність дорівнює одиниці, тобто подія відбуватиметься завжди. Отже, максимальне значення функції ймовірності дорівнює 1.

$f(x)\leq 1$

Нарешті, сума всіх значень функції ймовірності дає 1, оскільки це сума всіх ймовірностей у просторі вибірки.

$\displaystyle \sum_{i=1}^{+\infty}f(x_i)=\sum_{i=1}^{+\infty}p_i=1$

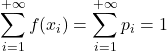
Приклад функції ймовірності

Тепер, коли ми знаємо визначення та характеристики функції ймовірності, давайте розглянемо приклад цього типу імовірнісної функції.

Обчисліть ймовірність отримання голів 0, 1, 2, 3 і 4 рази, виконавши чотири незалежні підкидання монети. Далі побудуйте графік знайденої функції ймовірності.

Перш за все, ми повинні розрахувати ймовірність отримання голів, для цього ми повинні розділити можливі випадки на загальну кількість випадків. Ви можете побачити розрахунок усіх ймовірностей у наступній таблиці:

І коли ми обчислили всі ймовірності, ми можемо представити значення функції ймовірності на графіку:

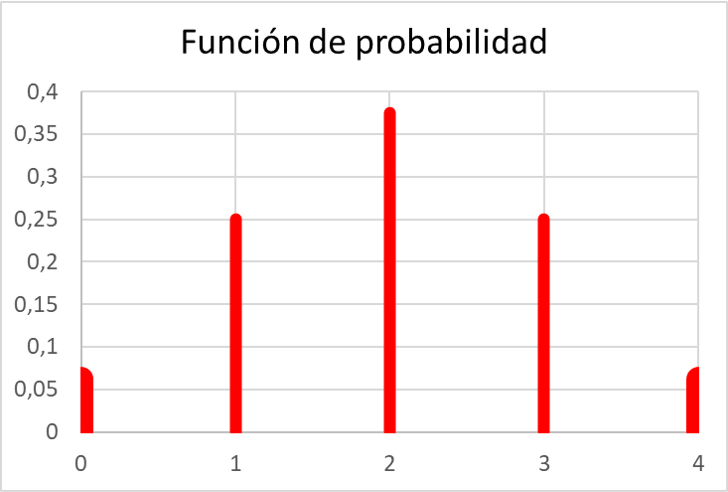
Як бачимо, імовірнісна функція у вправі відповідає всім властивостям функцій ймовірності, оскільки всі її значення знаходяться в межах від 0 до 1 і, крім того, сума всіх її значень еквівалентна 1.

Функція ймовірності та функція щільності

У цьому розділі ми побачимо різницю між функцією ймовірності та функцією щільності, оскільки це два типи імовірнісних функцій, які мають однакову мету, але використовуються в різних випадках.

Різниця між функцією ймовірності та функцією щільності полягає в типі змінної, для якої ймовірності описуються. Функція ймовірності використовується для визначення ймовірностей дискретної змінної, тоді як функція щільності використовується для визначення ймовірностей безперервної змінної.

Отже, залежно від змінної використовується функція ймовірності або функція щільності.

Щоб дізнатися більше про функцію щільності, натисніть таке посилання:

➤ Див.: функція щільності ймовірності

Функція ймовірності та функція розподілу

Різниця між функцією ймовірності та функцією розподілу полягає в типі ймовірності, який вони визначають. Функція ймовірності вказує ймовірність того, що змінна набуває певного значення, а функція розподілу описує кумулятивну ймовірність змінної.

Тому функція розподілу обчислюється з функції ймовірності.

Як приклад, за наступним посиланням ви можете побачити розрахунок функції розподілу для отримання голів від чотирьох підкинутих монет на основі функції ймовірності, знайденої у вправі вище.

➤ Див.: приклад функції розподілу

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше