Функція розподілу

за Редакція 5 Серпня, 2023 Ймовірність 0 коментарів

У цій статті ви знайдете пояснення функції розподілу, як обчислюються її значення та реальний приклад функції розподілу. Крім того, ви зможете побачити відмінності між функцією розподілу та функцією щільності.

Що таке функція розподілу?

Функція розподілу , також звана кумулятивною функцією розподілу , є математичною функцією, яка вказує кумулятивну ймовірність розподілу. Тобто образ функції розподілу для будь-якого значення дорівнює ймовірності того, що змінна приймає це значення або нижче значення.

Кумулятивну функцію розподілу також можна позначати абревіатурою FDA, хоча її звичайним символом є велика F.

Тому функція розподілу визначається такою формулою:

$F(x)=P[X\leq x]$

Як обчислити функцію розподілу

Потім ми пояснюємо, як обчислити значення функції розподілу залежно від того, дискретним чи неперервним є розподіл ймовірностей.

Стримана коробка

Якщо випадкова величина дискретна, кумулятивна функція розподілу дорівнює сумі ймовірностей усіх значень, що дорівнюють або менше х .

$\displaystyle F(x)=P[X\leq x]=\sum_{u\leq x}f(u)$

золото

$f(u)$

– функція ймовірності, пов’язана з дискретною змінною.

Триваюча справа

Якщо випадкова величина неперервна, кумулятивна функція розподілу еквівалентна інтегралу функції щільності від мінус нескінченності до відповідного значення.

$\displaystyle F(x)=P[X\leq x]=\int_{-\infty}^{x}f(u)du$

золото

$f(u)$

це функція щільності, пов’язана з безперервною змінною.

Приклад функції розподілу

Тепер, коли ми знаємо визначення функції розподілу, давайте розглянемо практичний покроковий приклад, щоб навчитися обчислювати значення функції розподілу.

Обчисліть функцію розподілу для випадкового експерименту підкидання монети чотири рази.

Щоб вирішити вправу, ви повинні спочатку обчислити всі ймовірності, пов’язані з кількістю голів, отриманих під час чотирьох підкидань монети:

Таким чином, оскільки це дискретна змінна, для визначення образів функції розподілу достатньо додати ймовірності до значення змінної, про яку йде мова:

$\begin{array}{l}F(X\leq 0)=f(0)=0,0625\\[4ex]\begin{aligned}F(X\leq 1)& =f(0)+f(1)\\[1.1ex] & =0,0625+0,25=0,3125\end{aligned}\\[6ex]\begin{aligned}F(X\leq 2)& =f(0)+f(1)+f(2)\\[1.1ex] & =0,0625+0,25+0,375=0,6875\end{aligned}\\[6ex]\begin{aligned}F(X\leq 3)& =f(0)+f(1)+f(2)+f(3)\\[1.1ex] & =0,0625+0,25+0,375+0,25=0,9375\end{aligned}\\[6ex]\begin{aligned}F(X\leq 4)& =f(0)+f(1)+f(2)+f(3)+f(4)\\[1.1ex] & =0,0625+0,25+0,375+0,25+0,0625=1\end{aligned}\end{array}$

Таким чином, значення функції розподілу підкидання голови шляхом підкидання чотирьох незалежних монет наступні:

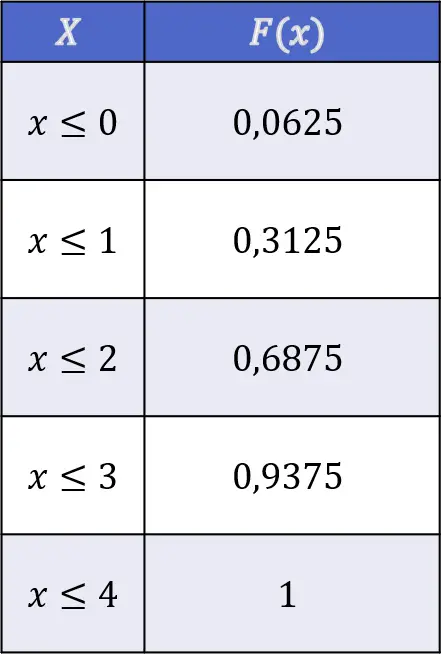
Властивості функції розподілу

Незалежно від типу змінної функція розподілу завжди має такі властивості:

Значення кумулятивної функції розподілу знаходиться в межах від 0 до 1 включно.

$0\leq F(x) \leq 1$

Межа функції розподілу при прагненні x до нескінченності дорівнює 1.

$\displaystyle\lim_{x\to +\infty} F(x)=1$

З іншого боку, межа функції розподілу, коли x наближається до мінус нескінченності, дорівнює нулю.

$\displaystyle\lim_{x\to -\infty} F(x)=0$

За своїми характеристиками функція розподілу є монотонною і неспадною.

$x_1 \leq x_2 \implies F(x_1)\leq F(x_2)$

Крім того, якщо
$a\leq b$

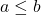
виконуються наступні рівняння.

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}P(X < a) = F(a^-)\\[2ex] P(X>a)=1-F(a)\\[2ex]P(X \ge a )=1-F(a^-)\\[2ex]P(a<ul><li> Finally, if the statistical variable is continuous, the following equality is satisfied: </li></ul>[latex ]\begin{array}{l}P(a \le X < b) = \displaystyle\int_{a}^{b}f(x)\,dx = F(b)- F(a)\end{array}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ... the statistical variable is continuous, the
Please use \mathaccent for accents in math mode.
leading text: ...iable statistic is continuous, equality
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}

Функція розподілу та функція густини

Нарешті, ми побачимо, яка різниця між функцією розподілу та функцією щільності, оскільки ці два статистичні поняття часто плутають.

Різниця між функцією розподілу та функцією щільності полягає в типі ймовірності, який вони визначають. Функція щільності описує ймовірність того, що змінна набуває певного значення, а функція розподілу описує кумулятивну ймовірність змінної.

Тобто функція розподілу використовується для обчислення ймовірності того, що змінна дорівнює або менше певного значення.

Зауважте, що функція щільності стосується лише неперервних змінних, тому це розрізнення має сенс, лише якщо змінна, що вивчається, є неперервною.

Зверніть увагу, як змінюється графічне представлення функції розподілу порівняно з функцією щільності змінної, яка відповідає нормальному розподілу із середнім значенням 1 і стандартним відхиленням 0,5:

різниця між функцією розподілу та функцією густини

Щоб дізнатися більше про функцію щільності, перегляньте цю статтю:

➤ Див.: функція щільності

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше