Що таке харчовий тест? (пояснення та приклад)

Тест Чоу — це статистичний тест, розроблений економістом Грегорі Чоу , який використовується для перевірки рівності коефіцієнтів двох різних регресійних моделей на різних наборах даних.

Тест Чоу зазвичай використовується в галузі економетрики з даними часових рядів, щоб визначити, чи існує структурний розрив у даних у певний момент часу.

Наприклад, розглянемо таку діаграму розсіювання:

Якби ми використовували лінію регресії для підсумовування моделі в даних, це могло б виглядати так:

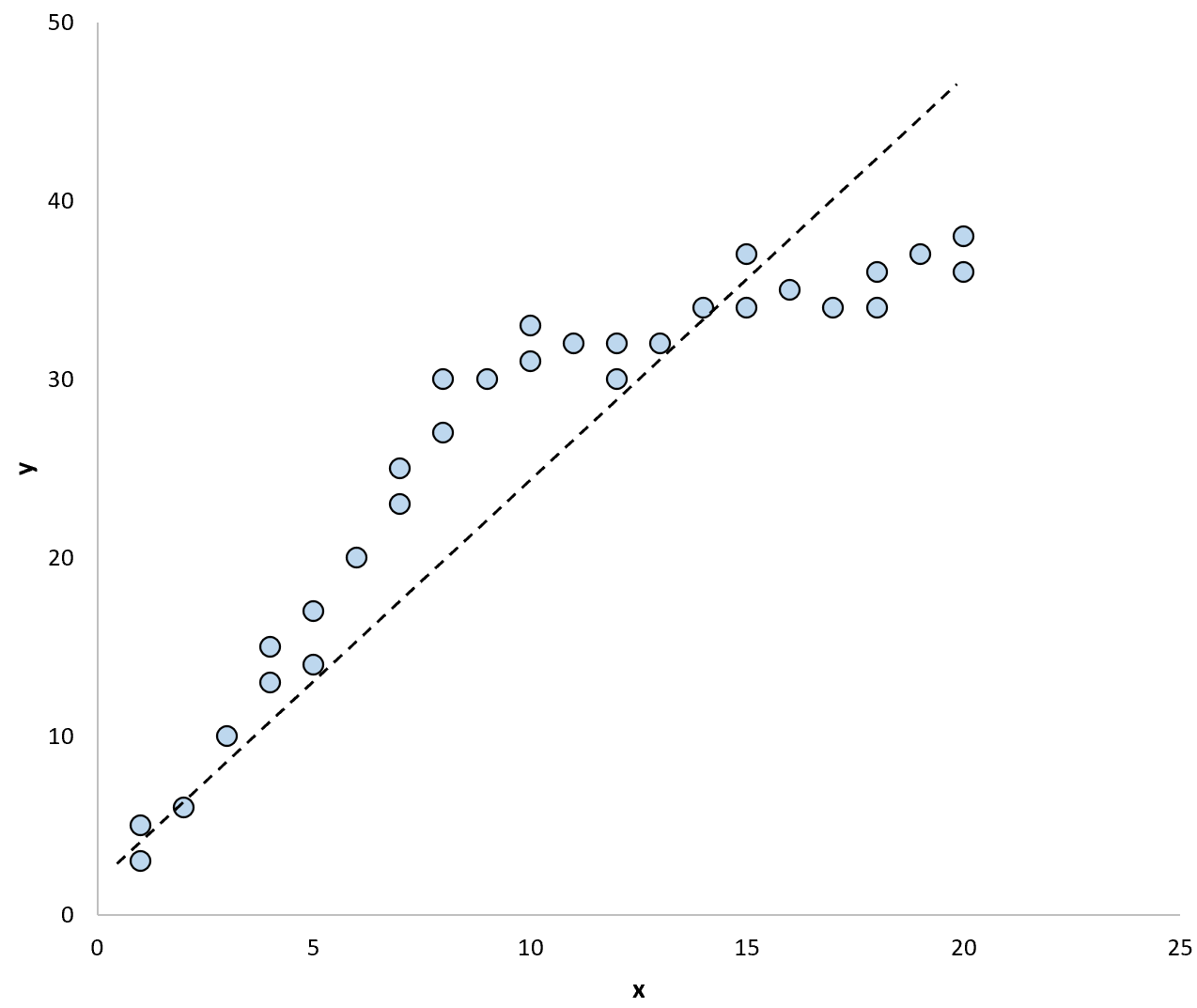
І якби ми використали дві окремі лінії регресії, щоб узагальнити модель у даних, це могло б виглядати так:

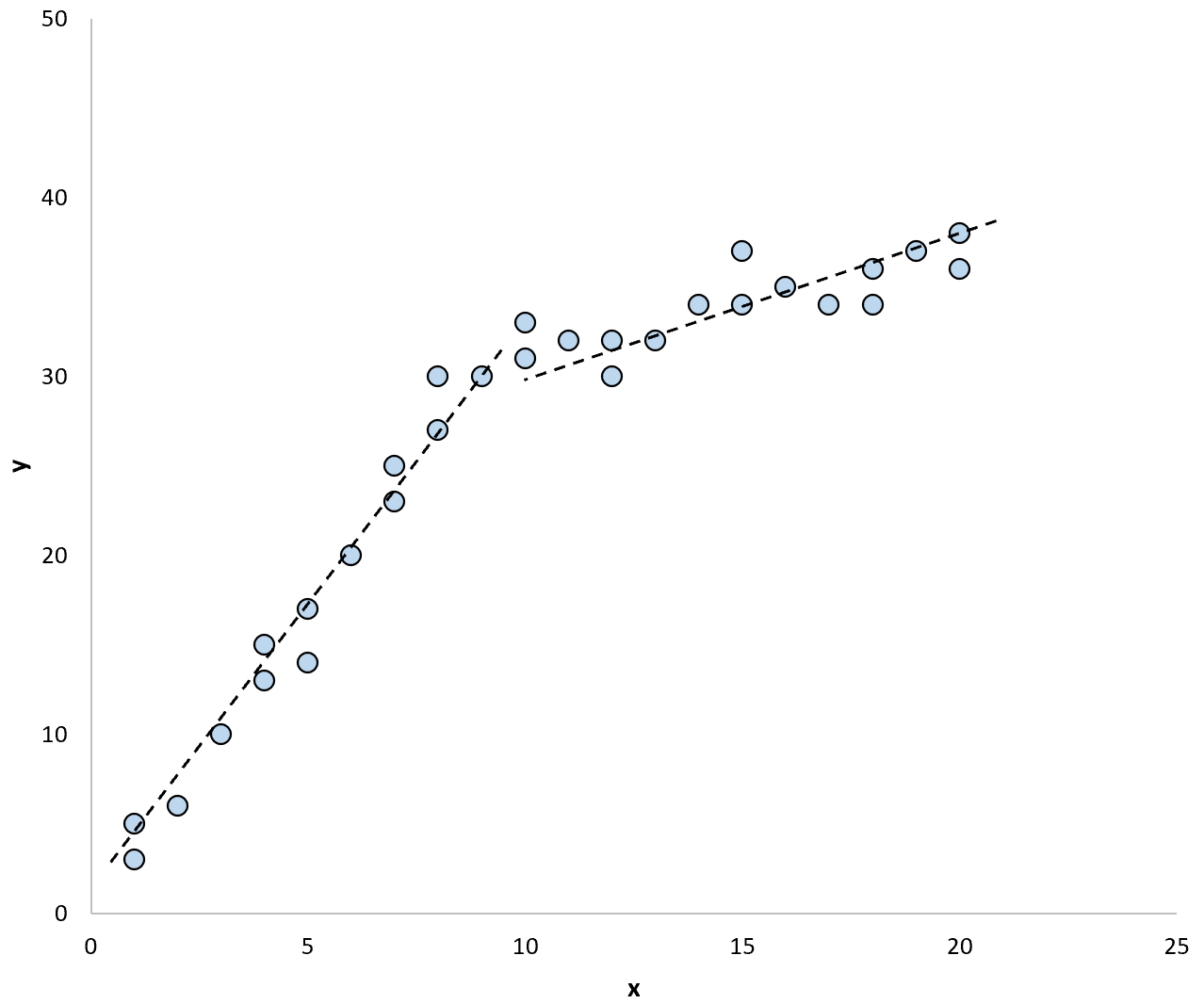
Тест Чоу дозволяє нам перевірити, чи рівні коефіцієнти регресії кожної лінії регресії.

Якщо тест визначає, що коефіцієнти між лініями регресії не збігаються, це означає, що є суттєві докази структурного розриву в даних. Іншими словами, тенденція даних дуже відрізняється до і після цього структурного перелому.

Коли використовувати тест Чоу

Наступні приклади ілюструють ситуації, у яких ви можете виконати тест Чоу:

1. Визначте, чи змінюються курси акцій до та після виборів.

2. Визначте, чи змінюються ціни на житло до і після зміни процентної ставки.

3. Визначте, чи відрізняється середній прибуток державних підприємств до та після прийняття нового податкового закону.

У кожній ситуації ми можемо використовувати тест Чоу, щоб визначити, чи існує структурна точка розриву в даних у будь-який момент часу.

Кроки для виконання тесту на їжу

Ми можемо використати наступні кроки, щоб виконати тест Чоу.

Крок 1: Визначте нульову та альтернативну гіпотези.

Припустімо, що ми адаптуємо таку модель регресії до всього нашого набору даних:

• y _t = a + bx _1t + cx _t2 + ε

Далі припустімо, що ми розділили наші дані на дві групи на основі структурної точки розриву та підібрали наступні моделі регресії до кожної групи:

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Ми б використали такі нульові та альтернативні гіпотези для тесту Чау:

• Нуль (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ і c ₁ = c ₂
• Альтернатива (H _A ): принаймні одне з порівнянь у Null не є рівним.

Якщо ми відхилимо нульову гіпотезу, у нас буде достатньо доказів, щоб стверджувати, що існує структурна точка зламу в даних і що дві лінії регресії можуть відповідати даним краще, ніж одна.

Якщо нам не вдасться відхилити нульову гіпотезу, у нас буде недостатньо доказів, щоб стверджувати, що в даних існує структурна точка зламу. У цьому випадку ми говоримо, що лінії регресії можна «звести» в одну лінію регресії, яка достатньо добре представляє модель даних.

Крок 2: Обчисліть статистику тесту.

Якщо ми визначимо такі терміни:

• S _T : сума квадратів залишків загальних даних
• S ₁ , S ₂ : сума квадратів залишків кожної групи
• N ₁ , N ₂ : кількість спостережень у кожній групі
• k: кількість параметрів

Тоді ми можемо сказати, що статистика тесту Чоу така:

Статистика тесту чау = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Ця тестова статистика відповідає розподілу F з k і N ₁ +N ₂ -2k ступенів свободи.

Крок 3: Відкиньте або не відкидайте нульову гіпотезу.

Якщо p-значення, пов’язане з цією тестовою статистикою, нижче за певний рівень значущості , ми можемо відхилити нульову гіпотезу та зробити висновок, що в даних існує структурна точка розриву.

На щастя, більшість статистичних програм здатні виконувати тест Чоу, тому вам, ймовірно, ніколи не доведеться виконувати тест вручну.

Приклад виконання тесту Чоу

Зверніться до цього підручника , щоб побачити покроковий приклад того, як виконати тест Chow для певного набору даних у R.

Примітки до тесту чау

Ось кілька приміток, про які слід пам’ятати про тест Чоу:

1. Тест припускає, що залишки регресійних моделей незалежно та однаково розподілені з нормального розподілу з невідомою дисперсією.

2. Тест Чау слід використовувати лише тоді, коли структурний розрив, який ви бажаєте перевірити, відбувається у відомий час. Іншими словами, тест не слід використовувати повторно, щоб визначити, чи можна вважати певний момент структурним розривом.