Як застосувати центральну граничну теорему в excel

Центральна гранична теорема стверджує, що вибірковий розподіл вибіркового середнього є приблизно нормальним, якщо розмір вибірки достатньо великий, навіть якщо розподіл сукупності не є нормальним .

Центральна гранична теорема також стверджує, що вибірковий розподіл матиме такі властивості:

1. Середнє значення розподілу вибірки дорівнюватиме середньому значенню розподілу сукупності:

x = µ

2. Стандартне відхилення розподілу вибірки дорівнюватиме стандартному відхиленню сукупності, поділеному на розмір вибірки:

s = σ / √n

У цьому посібнику ми пояснюємо, як застосувати центральну граничну теорему в Excel до даного розподілу.

Застосування центральної граничної теореми в Excel

Припустимо, ми маємо розподіл із середнім значенням 8 і стандартним відхиленням 4 . Ми можемо використовувати такі формули в Excel, щоб знайти як середнє, так і стандартне відхилення розподілу вибірки з розміром вибірки 15 :

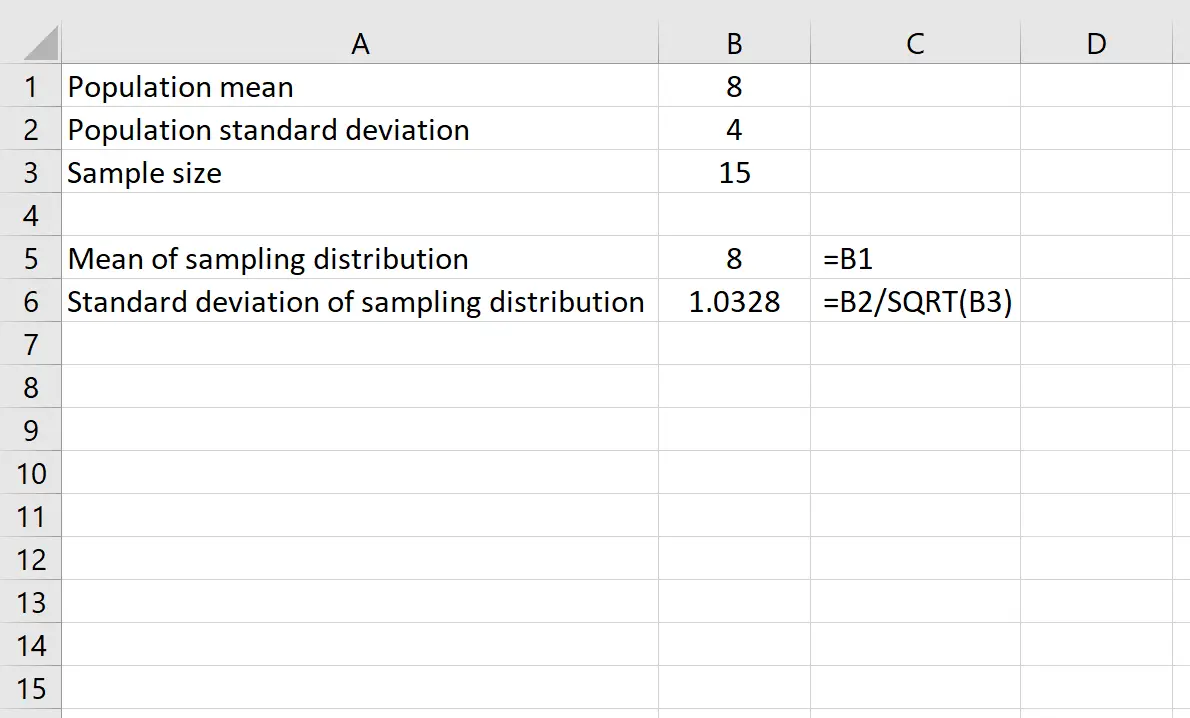
Середнє значення розподілу вибірки просто дорівнює середньому значенню розподілу сукупності, яке дорівнює 8 .

Стандартне відхилення розподілу вибірки дорівнює стандартному відхиленню сукупності, поділеному на розмір вибірки, або: 4 /√15 = 1,0328 .

Ми також можемо використовувати центральну граничну теорему, щоб відповісти на питання про ймовірність. Наприклад, якщо дана сукупність має середнє значення 8 і стандартне відхилення 4 , яка ймовірність того, що дана вибірка розміром 15   має середнє менше або дорівнює 7 ?

Щоб відповісти на це запитання, ми можемо використати функцію NORM.DIST() в Excel, яка використовує такий синтаксис:

NORM.DIST(x, середнє, standard_dev, кумулятивний)

золото:

• x: зразок означає, що ви хочете перевірити
• середнє значення: очікуване середнє значення розподілу вибірки
• standard_dev: очікуване стандартне відхилення розподілу вибірки
• кумулятивний: TRUE повертає нормальне значення CDF; FALSE повертає значення звичайного PDF. У нашому випадку ми завжди будемо використовувати TRUE.

Ця функція поверне ймовірність того, що вибіркове середнє менше або дорівнює певному значенню.

Ось формула, яку ми будемо використовувати в цьому прикладі:

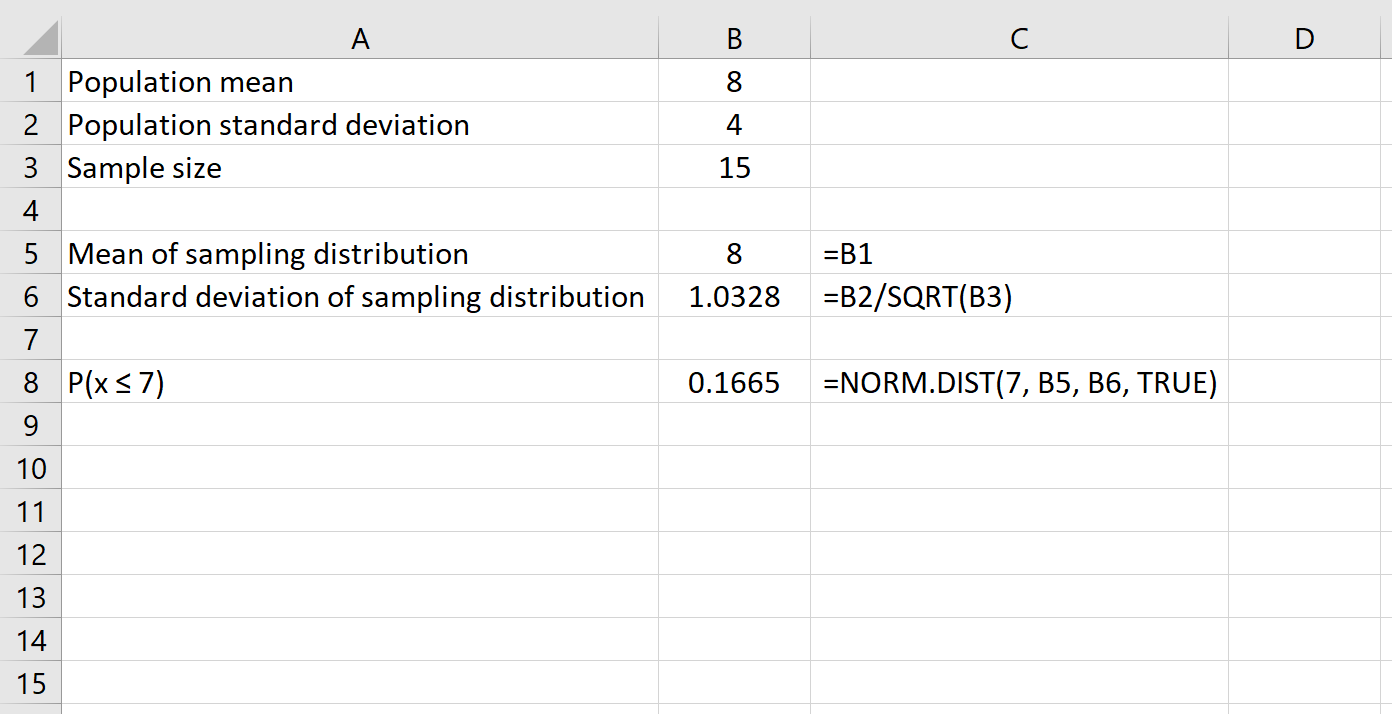
Це говорить нам про те, що для сукупності із середнім значенням 8 і стандартним відхиленням 4 ймовірність того, що дана вибірка розміром 15   має середнє менше або дорівнює 7 або 0,1665 .

Ми також можемо знайти ймовірність того, що заданий розмір вибірки матиме середнє значення більше певного числа, просто використовуючи формулу 1 – NORM.DIST() .

Наприклад, наведена нижче формула показує, як визначити ймовірність того, що заданий розмір вибірки 15 матиме середнє значення більше 7:

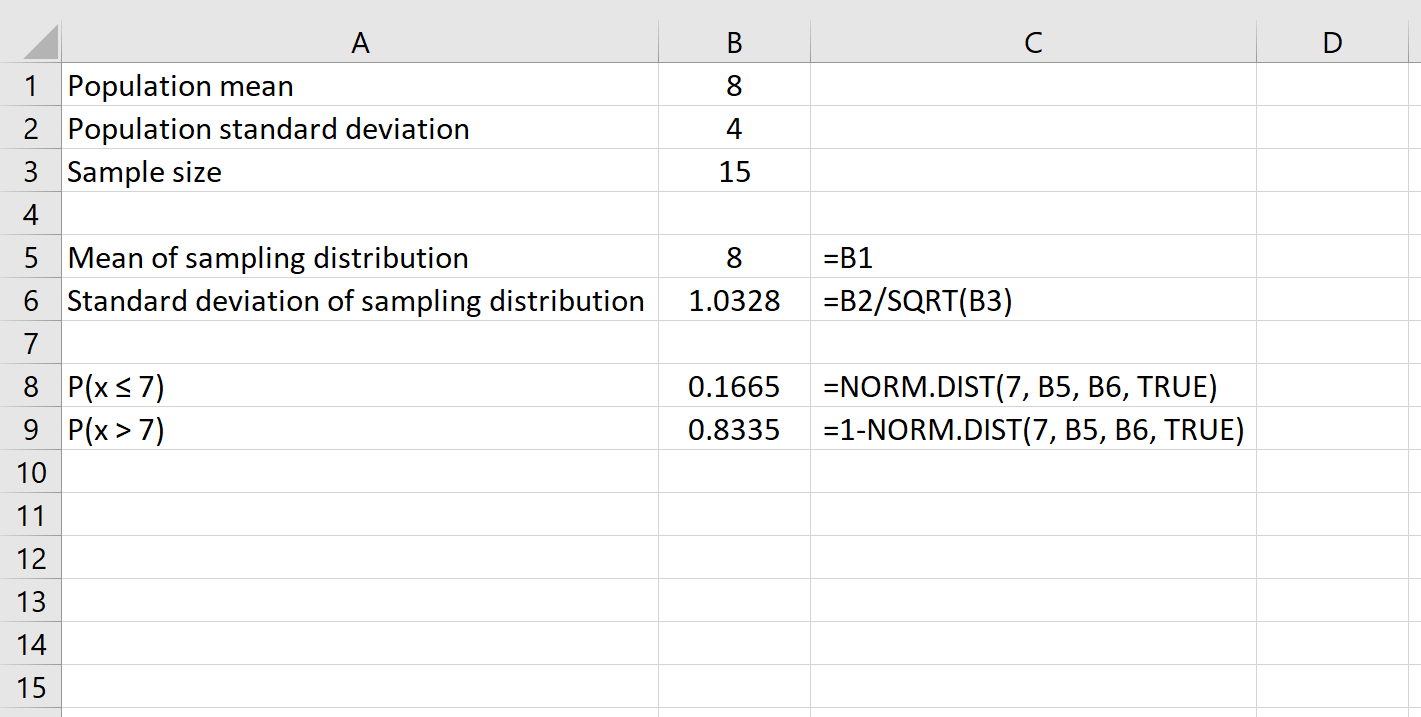
Нарешті, ми можемо знайти ймовірність того, що заданий розмір вибірки має середнє значення між двома числами за допомогою формули NORM.DIST(більше число) – NORM.DIST(менше число) .

Наприклад, наступна формула показує, як знайти ймовірність того, що заданий розмір вибірки 15 має середнє значення між 7 і 9:

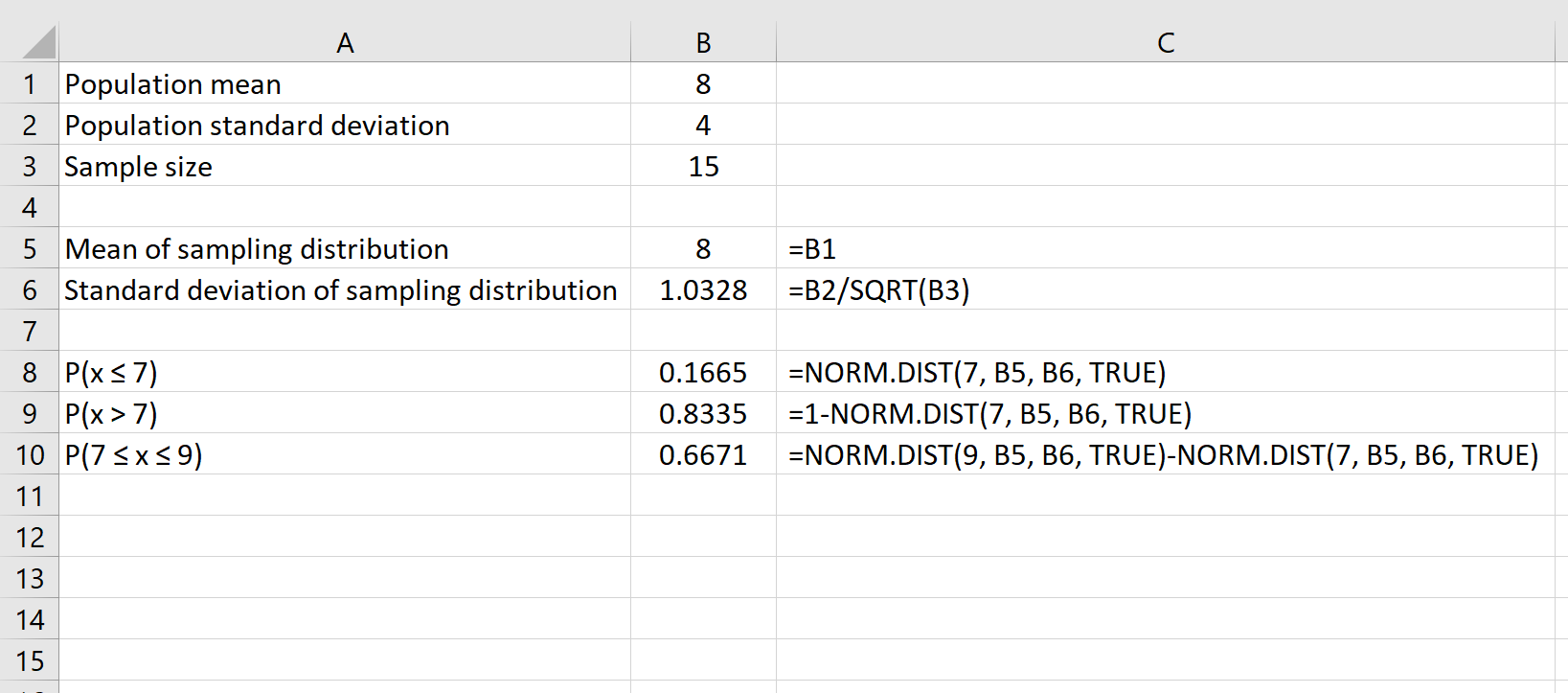
Додаткові ресурси

Калькулятор центральної граничної теореми
Як застосувати емпіричне правило в Excel
Як створити дзвоноподібну криву в Excel