Як застосувати центральну граничну теорему до калькулятора ti-84

Центральна гранична теорема стверджує, що вибірковий розподіл вибіркового середнього є приблизно нормальним, якщо розмір вибірки достатньо великий, навіть якщо розподіл сукупності не є нормальним.

Центральна гранична теорема також стверджує, що вибірковий розподіл матиме такі властивості:

1. Середнє значення розподілу вибірки дорівнюватиме середньому значенню розподілу сукупності:

x = µ

2. Стандартне відхилення розподілу вибірки дорівнюватиме стандартному відхиленню сукупності, поділеному на розмір вибірки:

s = σ / √n

Щоб знайти ймовірності, пов’язані з вибірковим середнім на калькуляторі TI-84, ми можемо використати функцію normalcdf() із таким синтаксисом:

 normalcdf (lower value, upper value, x , s/√ n )

золото:

• x : вибірка середніх
• s : вибіркове стандартне відхилення
• n : розмір вибірки

Щоб отримати доступ до цієї функції на калькуляторі TI-84, просто натисніть 2nd , потім натисніть VARS , потім прокрутіть до normalcdf ( і натисніть ENTER .

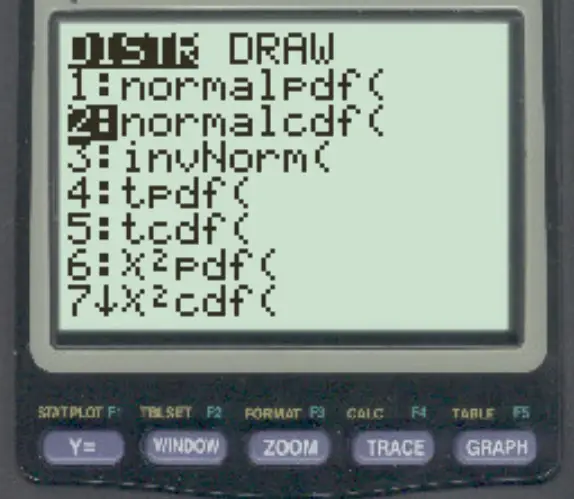
Наступні приклади показують, як використовувати цю функцію на практиці.

Приклад 1: Знайти ймовірність між двома значеннями

Розподіл має середнє значення 70 і стандартне відхилення 7. Якщо ми вибираємо випадкову вибірку розміром n = 35, знайдіть ймовірність того, що середнє значення вибірки буде між 68 і 72.

Ми можемо використовувати такий синтаксис на TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

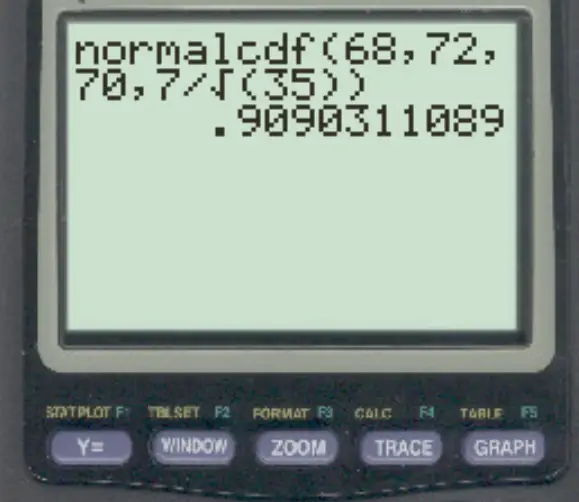
Імовірність того, що вибіркове середнє значення знаходиться між 68 і 72, становить 0,909 .

Приклад 2: Знаходження ймовірності, більшої за значення

Розподіл має середнє значення 50 і стандартне відхилення 4. Якщо ми вибираємо випадкову вибірку розміром n = 30, знайдіть ймовірність того, що середнє значення вибірки перевищує 48.

Ми можемо використовувати такий синтаксис на TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

Примітка. Ви можете отримати доступ до символу «E», натиснувши 2 , а потім кнопку , .

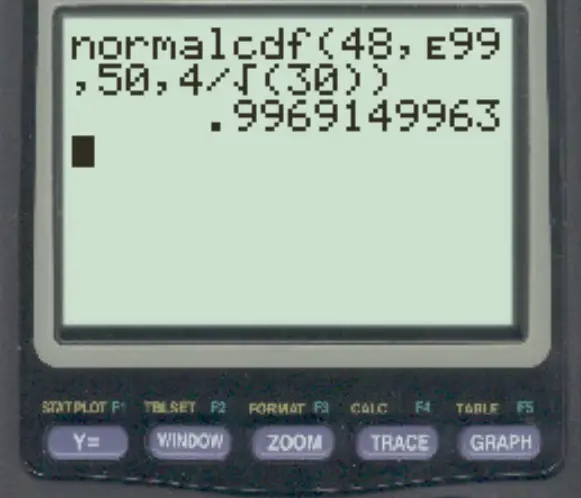
Імовірність того, що вибіркове середнє більше 48, становить 0,9969 .

Приклад 3: Знаходження ймовірності, меншої за значення

Розподіл має середнє значення 20 і стандартне відхилення 3. Якщо ми обираємо випадкову вибірку розміром n = 40, знайдіть ймовірність того, що середнє значення вибірки менше 19.

Ми можемо використовувати такий синтаксис на TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

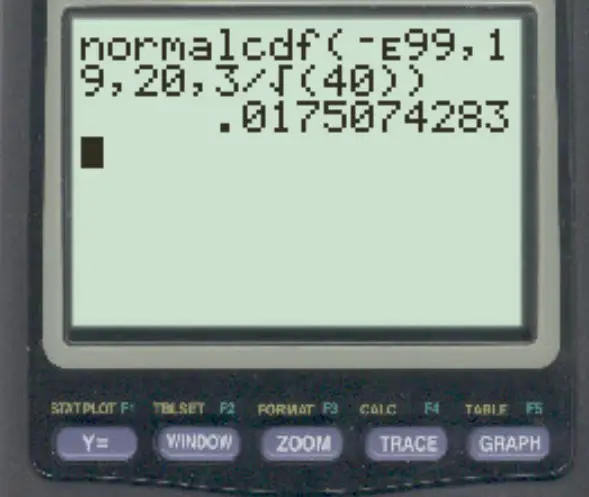
Імовірність того, що вибіркове середнє менше 19, становить 0,0175 .

Додаткові ресурси

Вступ до центральної граничної теореми
Калькулятор центральної граничної теореми
Як застосувати центральну граничну теорему в Excel
Центральна гранична теорема: чотири умови, які повинні бути виконані