Пропорція вибірки

У цій статті пояснюється, що таке пропорція вибірки в статистиці. Таким чином, ви дізнаєтесь, як розрахувати частку вибірки, розв’язану вправу, а також, яка різниця між часткою вибірки та часткою сукупності.

Яка частка вибірки?

Частка вибірки – це відношення успішних справ у вибірці до розміру вибірки. Тому, щоб обчислити частку вибірки, кількість успіхів у вибірці потрібно розділити на загальну кількість даних.

Символ пропорції зразка:

.

У статистиці при проведенні опитування зазвичай відомі не всі дані про сукупність, тому зазвичай проводиться дослідження репрезентативної вибірки, а потім зроблені висновки екстраполюються на всю сукупність. населення. Таким чином, вибіркова частка використовується для оцінки частки всієї сукупності. Нижче ми побачимо, як це робиться.

Приклад формули пропорції

Частка вибірки дорівнює кількості успішних випадків у вибірці, поділеній на розмір вибірки. Отже, формула для розрахунку вибіркової частки така:

золото:

• 

  є пропорцією зразка.

• 

  кількість успішних випадків у вибірці.

• 

  це загальна кількість елементів даних у вибірці.

Приклад розрахунку частки вибірки

Ознайомившись із визначенням вибіркової частки та її формулою, у цьому розділі ми розв’яжемо простий приклад, щоб ви могли побачити, як обчислюється вибіркова частка.

• Компанія виробляє іграшку та купує одну з її частин у іншої сторонньої компанії. Однак у партіях, які він купує, з’являються дефектні деталі, тому він вирішує провести статистичне дослідження, щоб з’ясувати частку деталей у хорошому стані та частку дефектів. Отже, ви замовляєте зразок із 1000 одиниць і знаходите 138 бракованих деталей. Яка частка частин у хорошому стані у зразку? А яка частка бракованих деталей у зразку?

Кількість непошкоджених деталей у зразку дорівнює 1000 мінус кількість дефектних деталей:

Отже, щоб знайти пропорцію зразка, ми застосовуємо формулу, яку бачили вище:

Таким чином, частка зразка деталей у хорошому стані становить 86,2%.

З іншого боку, частка бракованих деталей еквівалентна одиниці мінус частка хороших деталей:

Таким чином, частка дефектних деталей у вибірці становить 13,8%.

Частка вибірки та частка сукупності

Частка населення — це частка статистичної сукупності. Тобто пропорція популяції — це відношення випадків успіху досліджуваної популяції по відношенню до всіх елементів, які є частиною зазначеної популяції.

Таким чином, різниця між національною пропорцією та пропорцією населення полягає в тому, що національна пропорція є пропорцією випадків більшості, у зміні пропорція населення відноситься до пропорції подій, що стосуються всіх елементів Населення.

Щоб відрізнити вибіркову частку від частки сукупності, їх позначають різними символами. Символ пропорції зразка:

, тоді як символ частки населення є

.

Загалом, пропорцію популяції неможливо визначити точно, оскільки не всі значення популяції зазвичай відомі. Натомість значення частки населення зазвичай оцінюється за допомогою довірчого інтервалу за такою формулою:

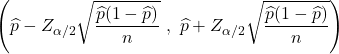
Щоб побачити, як оцінюється частка населення, натисніть на таке посилання:

Вибірковий розподіл пропорцій

Нарешті, ми побачимо, з чого складається вибірковий розподіл пропорцій, оскільки це статистична концепція, пов’язана з пропорцією вибірки.

По-перше, давайте почнемо з визначення того, що таке розподіл вибірки. Вибірковий розподіл — це розподіл, який є результатом урахування всіх можливих вибірок із статистичної сукупності.

Таким чином, вибірковий розподіл пропорцій – це розподіл, який є результатом обчислення частки кожної можливої вибірки з сукупності. Тобто, якщо ми вивчаємо всі можливі вибірки з сукупності та обчислюємо частку кожної з вибірок, розрахований набір значень є вибірковим розподілом пропорцій вибірки.