Як розрахувати часткову кореляцію в excel
У статистиці ми часто використовуємо коефіцієнт кореляції Пірсона для вимірювання лінійної залежності між двома змінними. Однак інколи ми хочемо зрозуміти зв’язок між двома змінними , контролюючи третю змінну .
Наприклад, припустімо, що ми хочемо виміряти зв’язок між кількістю годин навчання студента та оцінкою підсумкового іспиту, контролюючи при цьому поточну оцінку студента в класі. У цьому випадку ми могли б використати часткову кореляцію для вимірювання зв’язку між вивченими годинами та оцінкою підсумкового іспиту.
У цьому посібнику пояснюється, як обчислити часткову кореляцію в Excel.
Приклад: часткова кореляція в Excel
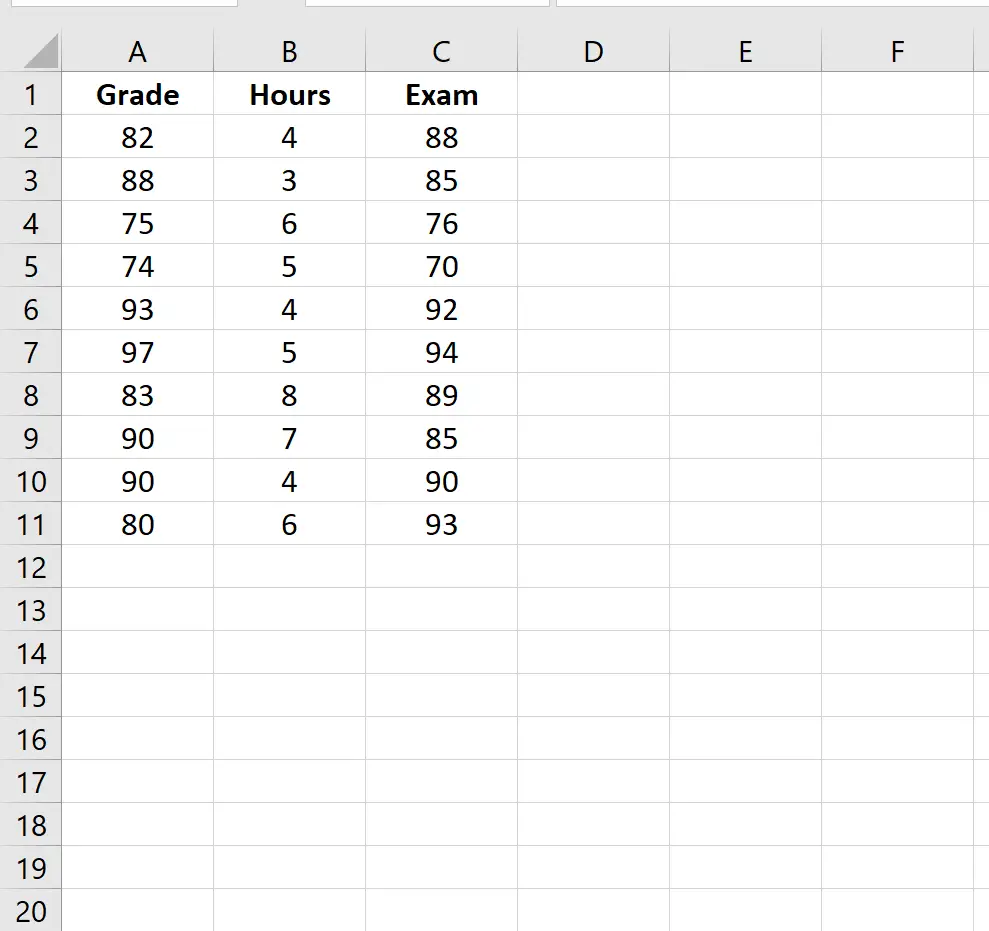
Припустімо, у нас є набір даних, який відображає таку інформацію про 10 студентів:
- Поточна оцінка в класі
- Години, витрачені на підготовку до випускного іспиту
- Оцінка підсумкового іспиту
Виконайте наступні кроки, щоб знайти часткову кореляцію між вивченими годинами та оцінкою іспиту з урахуванням поточної оцінки.
Крок 1: обчисліть кожну попарну кореляцію.
Спочатку ми обчислимо кореляцію між кожною попарною комбінацією змінних:
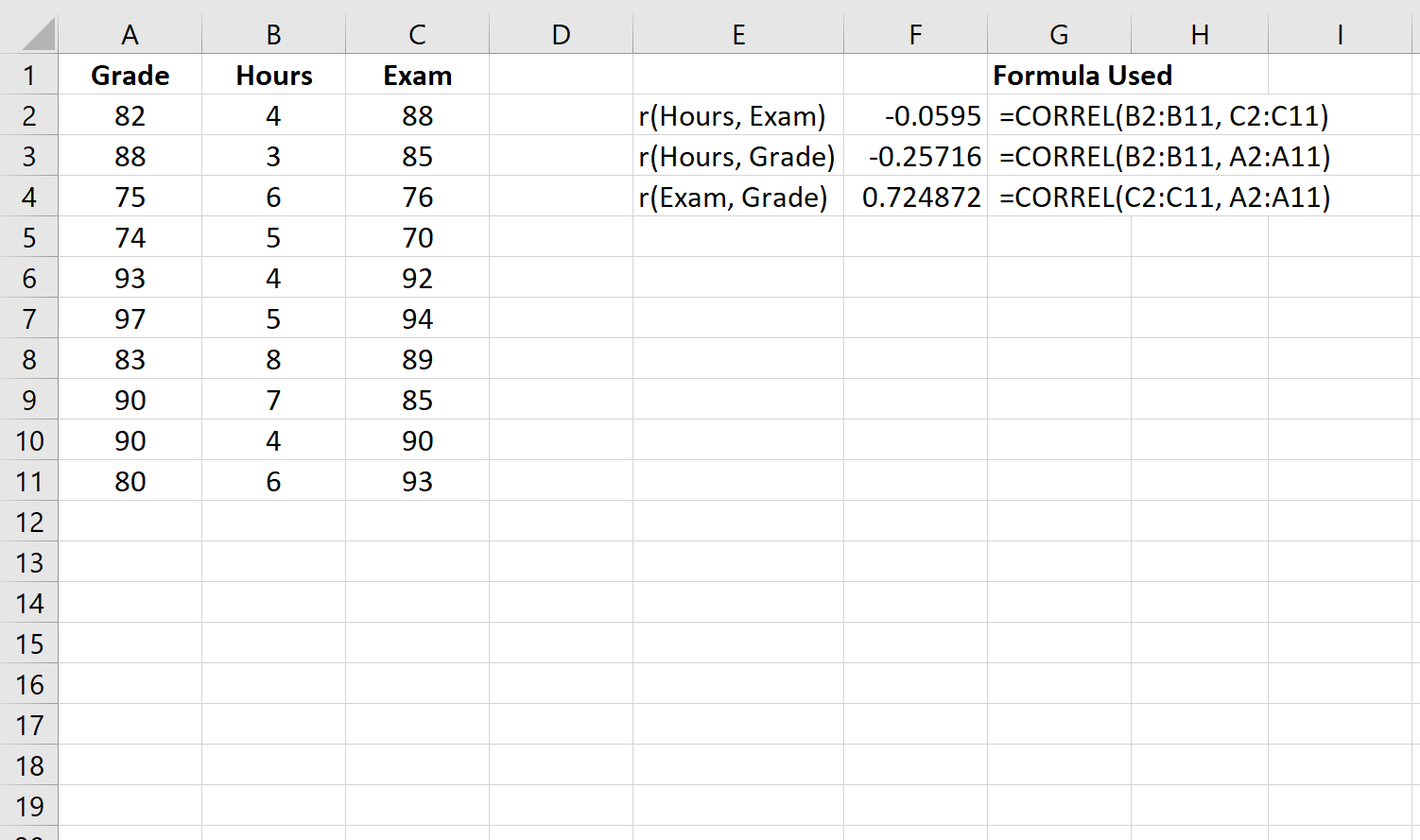
Крок 2: обчисліть часткову кореляцію між годинами та результатом іспиту.
Формула для обчислення часткової кореляції між змінною A та змінною B з урахуванням змінної C виглядає наступним чином:
Часткова кореляція = (r A,B – r A,C *r B,C ) / √((1-r 2 A,B )(1-r 2 B,C ))
На наступному знімку екрана показано, як використовувати цю формулу для обчислення часткової кореляції між годинами та оцінкою іспиту з урахуванням поточної оцінки:
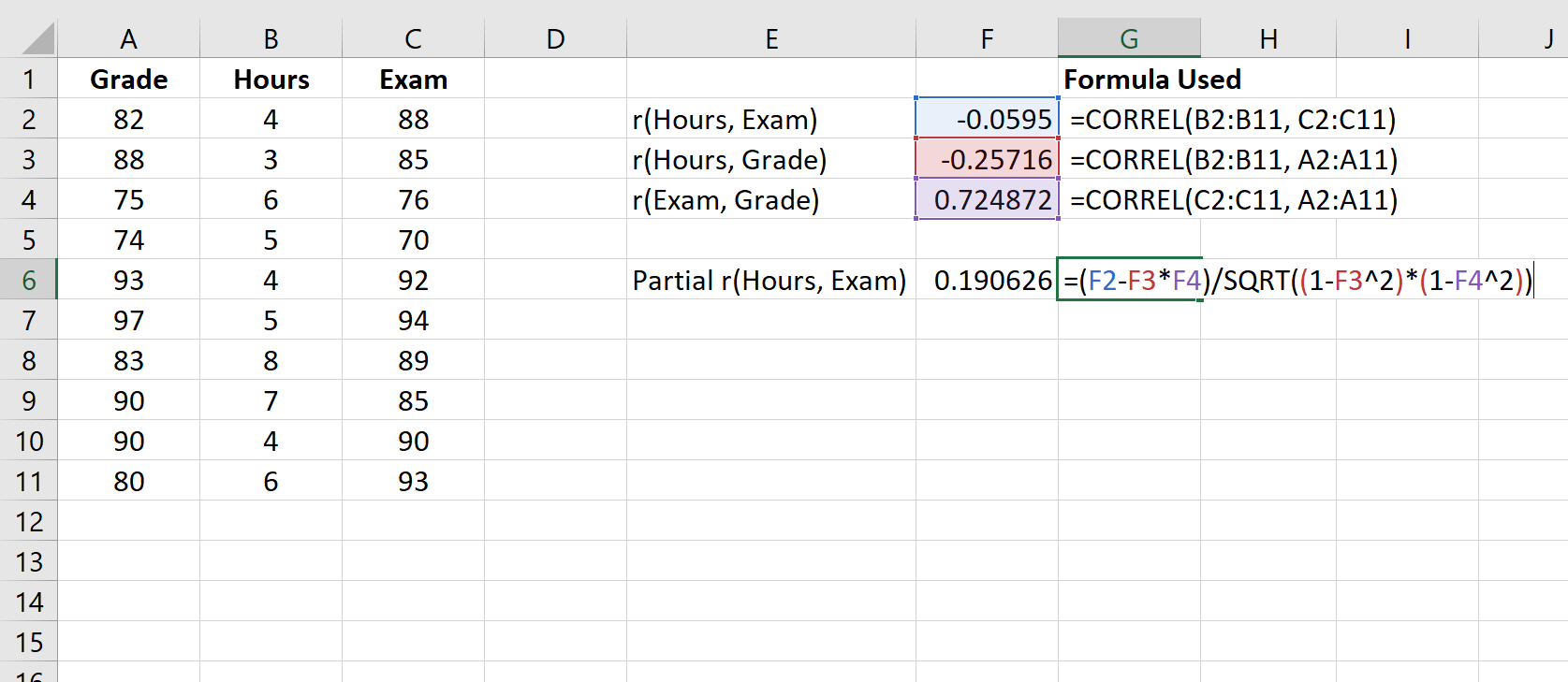
Часткова кореляція становить 0,190626 . Щоб визначити, чи ця кореляція є статистично значущою, ми можемо знайти відповідне значення p.
Крок 3: Обчисліть p-значення часткової кореляції.
Статистику t- критерію можна розрахувати наступним чином:
t = r√(n-3) / √(1-r 2 )
На наступному знімку екрана показано, як використовувати цю формулу для обчислення тестової статистики та відповідного p-значення:
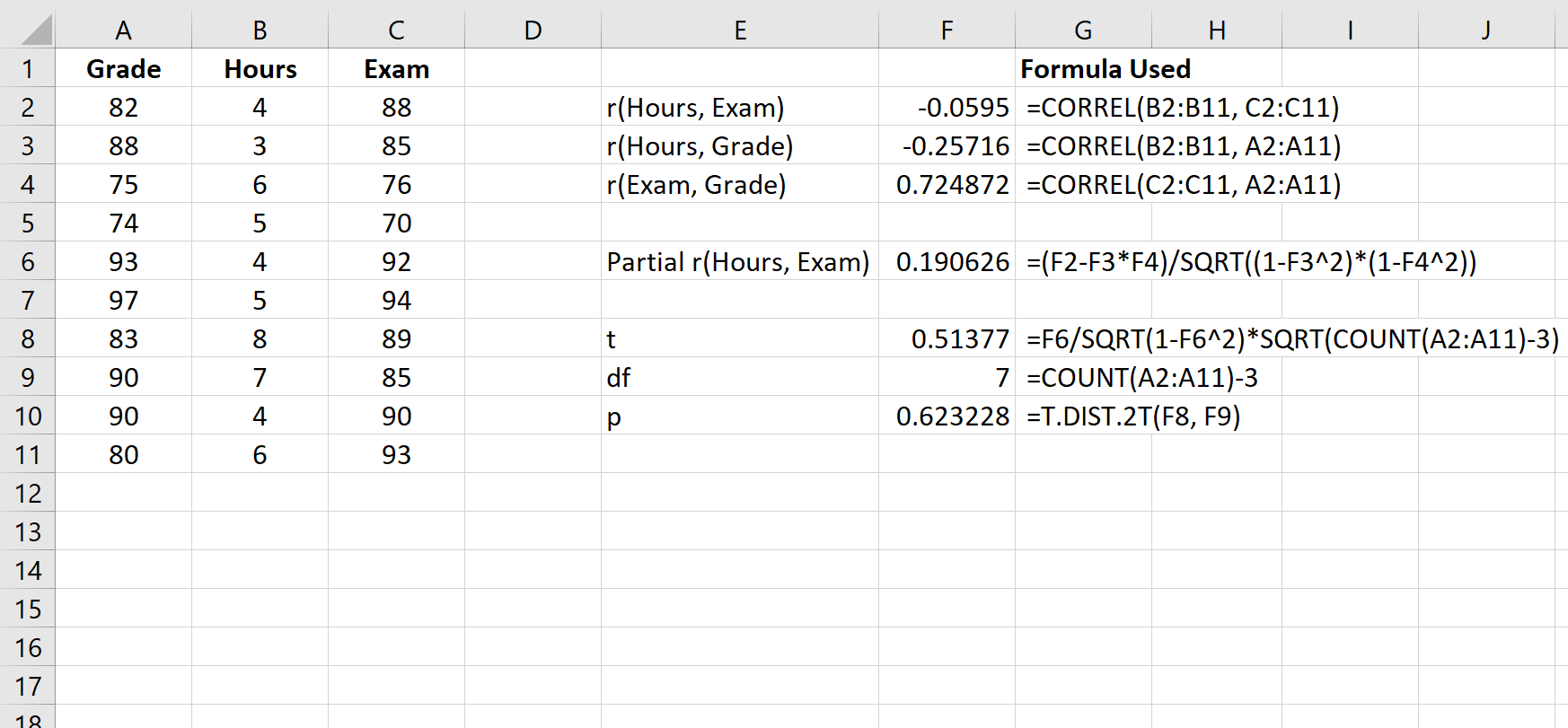
Статистика t- тесту становить 0,51377 . Загальна кількість ступенів свободи n-3 = 10-3 = 7 . Відповідне значення p становить 0,623228 . Оскільки це значення не менше 0,05, це означає, що часткова кореляція між годинами та результатами іспиту не є статистично значущою.